
脉冲响应不变法(ImpulseInvariance)·基本原理·脉冲响应不变法设计DF的步骤·H(2)的确定·MATLAB计算脉冲响应不变法的H(z)2025/7/2信息工程学院
2025/7/2 信息工程学院 •基本原理 •脉冲响应不变法设计DF的步骤 •H(z)的确定 •MATLAB计算脉冲响应不变法的H(z) 脉冲响应不变法(Impulse Invariance)

基本原理h[k] = h(t)| =kTH(ej2)和H(jの)的关系H(ej2)=(1/T) Z H(j(Q-2元n)/T)n=-00H(ei0)=(1/T)H(Gj2),[2|≤元无混叠时:T数字滤波器在Q点的频响特性和模拟滤波器の=Q/T频响特性只差一个常数因子2025/7/2信息工程学院
2025/7/2 信息工程学院 t kT h k h t = = [ ] ( ) H(ejW)和H(jw)的关系: H T H( n T ) n (e ) (1/ ) j( 2π )/ j = − =− W W 无混叠时: (e ) (1/ ) (j ), π j = W W W T H T H 数字滤波器在W点的频响特性和模拟滤波器w = W/ T频 响特性只差一个常数因子 基本原理
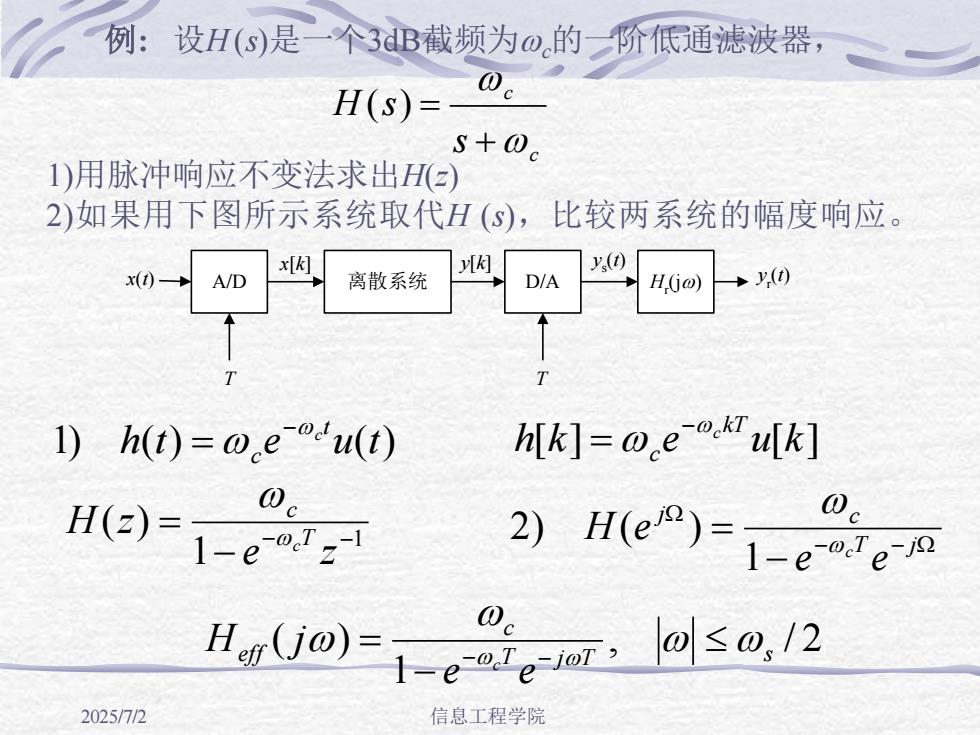
例:设H(s)是一个3dB截频为.的一阶低通滤波器0.H(s)=s+0.1)用脉冲响应不变法求出H)2)如果用下图所示系统取代H(s),比较两系统的幅度响应。y(t)[K]x[K]y(0)x(t) →A/DD/A离散系统H(jo)TTTh[k] = 0,e-0,T u[k]1)h(t) = w,e-ocu(t)0c0cH(z)=2)H(ej?)1-e-0 ,-11 -e-o.T e-jQ0cHer(jo)≤0, /2-e-ole-joT 2025/7/2信息工程学院
2025/7/2 信息工程学院 例: 设H (s)是一个3dB截频为wc的一阶低通滤波器, c c s H s w w + ( ) = 1)用脉冲响应不变法求出H(z) 2)如果用下图所示系统取代H (s),比较两系统的幅度响应。 1) h(t) e u(t) t c w −wc = h[k] e u[k] kT c w −wc = 1 1 ( ) − − − = e z H z T c wc w − − W W − = T j j c e e H e wc w 1 2) ( ) , / 2 1 ( ) T j T s c eff e e H j c w w w w w w − = − − x(t) A/D 离散系统 D/A x[k] Hr (jw) y[k] T ys (t) yr (t) T

0H(ss+o.1-e-orHeff nor0≤0, / 20-e-Te-joT ,wc=2*pi*5;fs=50;ws=2*pi*fs;T=1/fs ;f=linspace(0,fs/2, 512) ;f1=linspace(0,fs/2, 512) ;C=(1-exp(-wc*T)) ;Heff=C./(1-exp(-wc*T)*exp(-j*2*pi*f*T)) ;Ha=wc./ (j*2*pi*f1+wc) ;plot(f,abs(Heff),fl,abs(Ha));grid;xlabel('Hz');legend(Heff,Ha);2025/7/2信息工程学院
2025/7/2 信息工程学院 wc=2*pi*5;fs=50; ws=2*pi*fs;T=1/fs; f=linspace(0,fs/2, 512); f1=linspace(0,fs/2, 512); C=(1-exp(-wc*T)); Heff=C./(1-exp(-wc*T)*exp(-j*2*pi*f*T)); Ha=wc./(j*2*pi*f1+wc); plot(f,abs(Heff),f1,abs(Ha));grid; xlabel('Hz'); legend('Heff','Ha'); c c s H s w w + ( ) = , / 2 1 1 ( ) eff_nor T j T s T e e e H c c w w w w w w − − = − − −
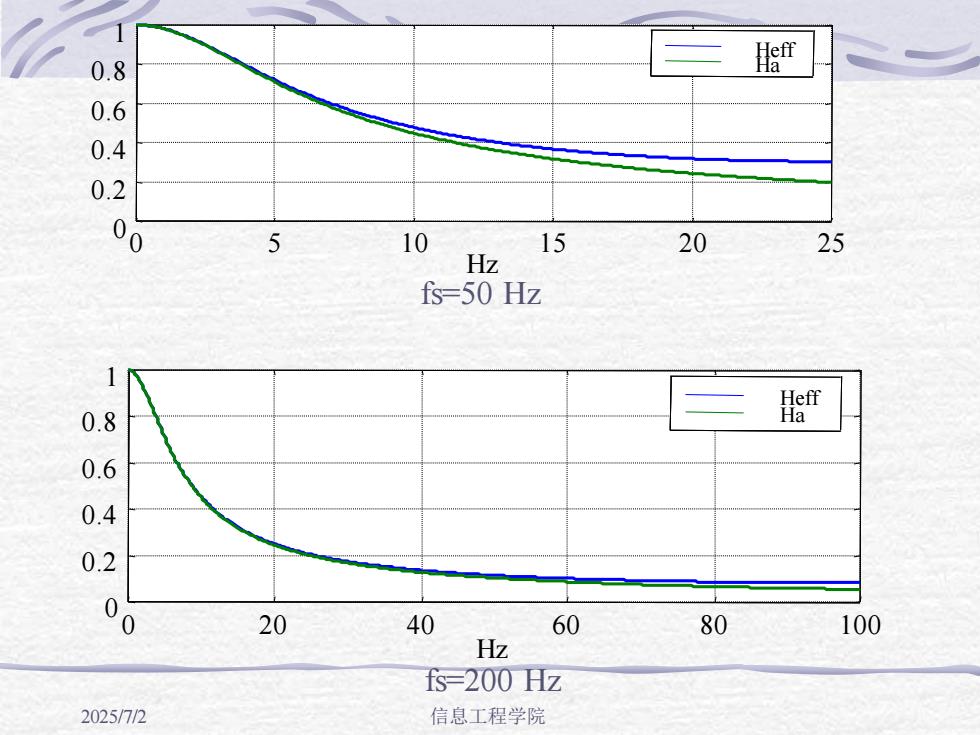
门Hafr0.80.60.40.2%515251020Hzfs=50Hz1HeffHa0.80.60.40.20020406080100Hzfs-200Hz信息工程学院2025/7/2
2025/7/2 信息工程学院 0 5 10 15 20 25 0 0.2 0.4 0.6 0.81 Hz Heff Ha fs=50 Hz 0 20 40 60 80 100 0 0.2 0.4 0.6 0.81 Hz Heff Ha fs=200 Hz