《数字信号处理》课程教学课件（PPT讲稿）ch4_4 双线性变换法

双线性变换法·变换推导·Q和の的关系·用MATLAB计算双线性变换MATLAB设计数字Butterworthfilten·MATLAB中IIR设计的主要函数

• 变 换 推 导 • W和w 的关系 •用MATLAB计算双线性变换 •MATLAB设计数字Butterworth filter •MATLAB中IIR设计的主要函数 双线性变换法

例：用脉冲响应不变法和一阶巴特沃思低通滤波器，设计的3dB截频为2,的数字滤波器为1-e-αpH(z)1 - e -2p z-1Wp1=0.2*pi;Wp2=0.6*pib1=[1-exp(-Wp1)];a1=[1 -exp(-Wp1)] ;b2=[1-exp(-Wp2) ];a2=[1 -exp(-Wp2)］ ;w=linspace(0,pi,512);hl=fregz(bl,al,w);h2=fregz(b2,a2,w)plot(w/pi,20*logl0（abs（hl)），w/pi,20*logl0（abs(h2)））xlabel（'Normalized frequency');ylabel（'Gain,db');grid;

p 1 p 1 e 1 e ( )       z H z W W 例:用脉冲响应不变法和一阶巴特沃思低通滤波器，设计的 3dB截频为Wp的数字滤波器为 Wp1=0.2*pi;Wp2=0.6*pi; b1=[1-exp(-Wp1)];a1=[1 -exp(-Wp1)]; b2=[1-exp(-Wp2)];a2=[1 -exp(-Wp2)]; w=linspace(0,pi,512); h1=freqz(b1,a1,w); h2=freqz(b2,a2,w); plot(w/pi,20*log10(abs(h1)),w/pi,20*log10(abs(h2)) ); xlabel('Normalized frequency'); ylabel('Gain,db'); grid;

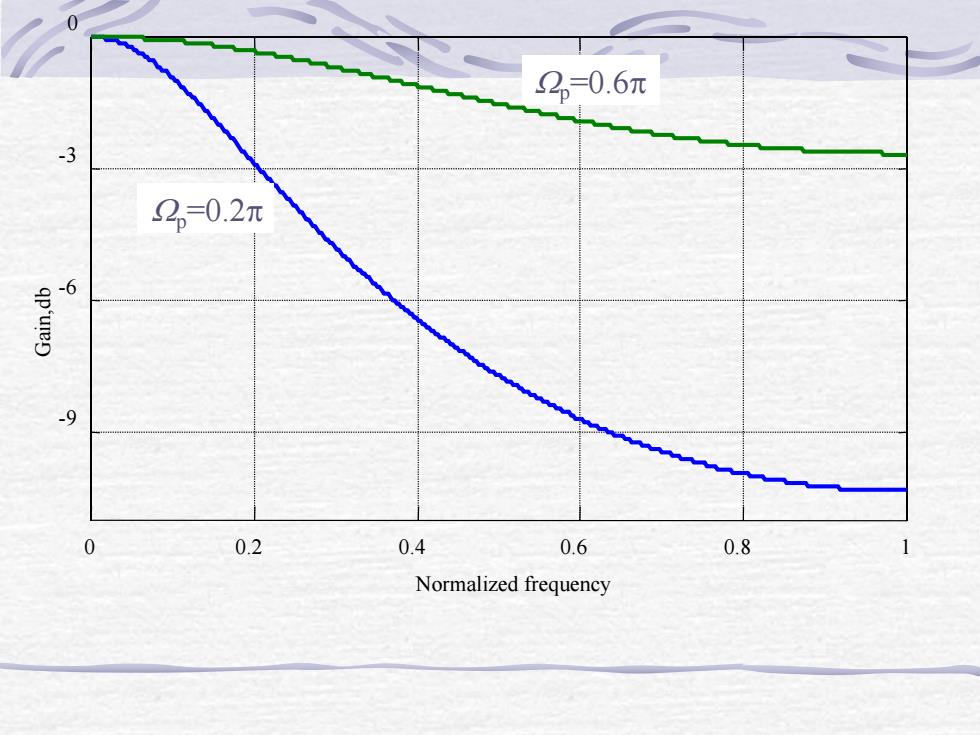
02=0.6元-32=0.2元-6e-900.60.20.40.8Normalized frequency

0 0.2 0.4 0.6 0.8 1 -9 -6 -3 0 Normalized frequency G ain,db Wp =0.2p Wp =0.6p

变换推导基本思想：利用数值积分将模拟系统变换为数字系统设模拟系统的微分方程为dy(t)= x(t) -ay(t)dtkTkTdy(t)t = y(kT)-y(k-1)T) ={ (x(t) -ay(t)dtdt(k-1)T(k-1)T用梯形面积近似计算等式右边的积分得y(kT)-y(k -1)T)=(T / 2)(x(kT) - ay(kT)+x(k-1)T)-ay(k -1)T))

变 换 推 导 基本思想: 利用数值积分将模拟系统变换为数字系统。 设模拟系统的微分方程为 ( ) ( ) d d ( ) x t ay t t y t   dt y kT y k T  dt dy t kT k T ( ) ( 1) ( ) ( 1)      x t ay t dt kT k T ( ( ) ( )) ( 1)     用梯形面积近似计算等式右边的积分得   T x kT ay kT x k T  ay k T  y kT y k T ( / 2) ( ) ( ) ( 1) ( 1) ( ) ( 1)        

y(kT)-y(k -1)T)=(T /2)(x(kT)-ay(kT)+ x(k -1)T)-ay(k -1)T)所以近似描述离散系统的差分方程为(1+aT /2)y[k]-(1-aT /2)y[k -1] =(T /2)(x[k]+ x[k -1)离散系统的系统函数为：1(T /2)(1+z-1)H(2)=-2 1-2-1(1+aT /2)-(1-aT /2)z-l+a1T 1+z和模拟系统的系统函数比较可得H(z)=H(s)2 1-2-1T 1+≥-1

所以近似描述离散系统的差分方程为 (1 aT / 2) y[k] (1 aT / 2) y[k 1]  (T / 2)x[k] x[k 1) 离散系统的系统函数为： a z z T aT aT z T z H z              1 1 1 1 1 2 1 1 (1 / 2) (1 / 2) ( / 2)(1 ) ( ) 和模拟系统的系统函数比较可得 1 1 1 2 1 ( ) ( )       z z T s H z H s   T x kT ay kT x k T  ay k T  y kT y k T ( / 2) ( ) ( ) ( 1) ( 1) ( ) ( 1)        