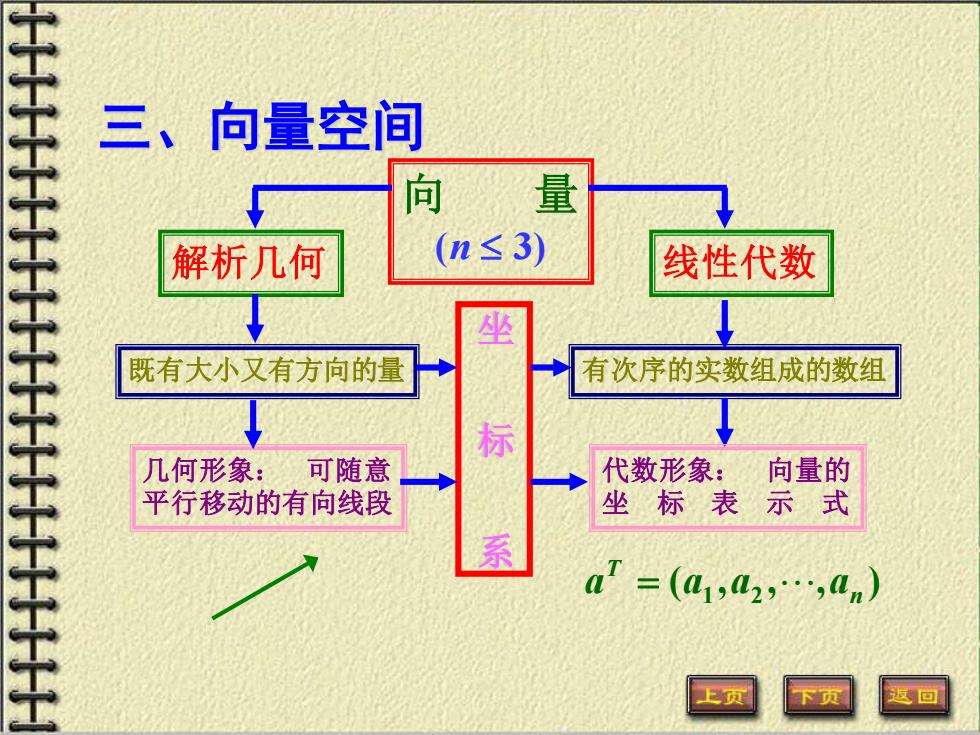
三、向量空间 向 解析几何 (n≤3) 线性代数 坐 既有大小又有方向的量 有次序的实数组成的数组 标 几何形象:可随意 代数形象:向量的 平行移动的有向线段 坐标表 示式 aT=(a1,2,an) 回
向 量 解析几何 (n 3) 线性代数 既有大小又有方向的量 有次序的实数组成的数组 几何形象: 可随意 平行移动的有向线段 代数形象: 向量的 坐 标 表 示 式 ( , , , ) 1 2 n T a = a a a 坐 标 系 三、向量空间
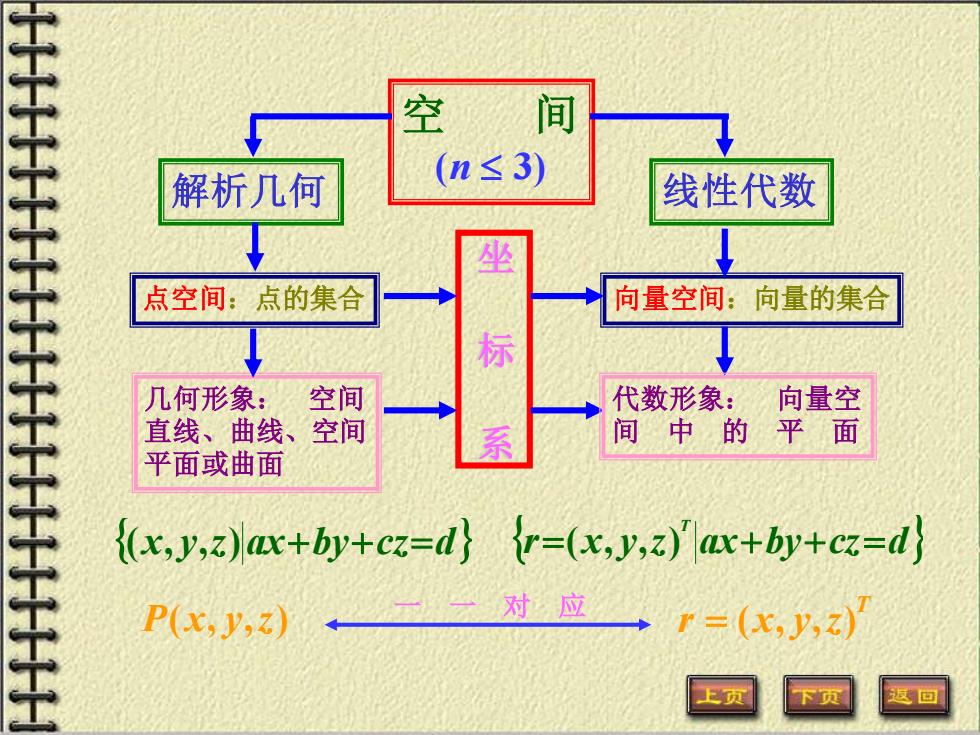
空 间 解析几何 (n≤3) 线性代数 点空间:点的集合 向量空间:向量的集合 标 几何形象: 空间 代数形象: 向量空 直线、曲线、空间 间中的 平 面 平面或曲面 (x,y,z)ax+by+cz=d} r=(x,y,z)ax+by+cz=dj P(x,y,z) 对应 r=(x,⑦) 上页
空 间 (n 3) 解析几何 线性代数 点空间:点的集合 向量空间:向量的集合 坐 标 系 代数形象: 向量空 间 中 的 平 面 r x y z ax by cz d T =( , , ) + + = 几何形象: 空间 直线、曲线、空间 平面或曲面 (x, y,z)ax+by+cz=d P(x, y,z) r (x, y,z) T = 一 一 对 应

n>3时,n维向量没有直观的几何形象. R={c=(xx2,x)xx2,x.eR} 叫做n维向量空间. ==x)aa:++ax=b 叫做n维向量空间R”中的n-I维超平面. 上页 回
R x x x xn x x xn R n T = =( 1 , 2 , , ) 1 , 2 , , x x x xn a x a x an xn b T = =( 1 , 2 , , ) 1 1+ 2 2++ = 叫做 n 维向量空间. n 3 时, n 维向量没有直观的几何形象. 叫做 维向量空间 R 中的 维超平面. n n n − 1

n维向量的实际意义 确定飞机的状态,需 要以下6个参数: 机身的仰角 2 机翼的转角 机身的水平转角 (0≤0<2π) 飞机重心在空间的位置参数P(x,y,☑ 所以,确定飞机的状态,需用6维向量 a=(x,y,3,p,w,8) 上页
确定飞机的状态,需 要以下6个参数: 飞机重心在空间的位置参数P(x,y,z) 机身的水平转角 (0 2 ) 机身的仰角 ) 2 2 ( − 机翼的转角 (− ) 所以,确定飞机的状态,需用6维向量 a = (x, y,z,, , ) n 维向量的实际意义

课堂讨论 在日常工作、学习和生活中,有许多问题都 需要用向量来进行描述,请同学们举例说明. 上页 这回
课堂讨论 在日常工作、学习和生活中,有许多问题都 需要用向量来进行描述,请同学们举例说明.