
3.互感线圈的同名端 具有互感的线圈两端的电压包含自感电压和互感电 压。表达式的符号与参考方向和线圈绕向有关。对自感 电压,当山,i取关联参考方向,与Φ符合右螺旋定则, 其表达式为 =N验= 41= dt 上式说明,对于自感电压由于电压电流为同一线圈上的, 只要参考方向确定了,其数学描述便可容易地写出,可不用 考虑线圈绕向。对线性电感,用山,描述其特性,当山,取关联 方向时,符号为正;当山,为非关联方向时,符号为负
3. 互感线圈的同名端 具有互感的线圈两端的电压包含自感电压和互感电 压。表达式的符号与参考方向和线圈绕向有关。对自感 电压,当u, i 取关联参考方向,i与 符合右螺旋定则, 其表达式为 d d d d d d 1 1 11 1 11 11 t i L t Φ N t Ψ u = = = 上式说明,对于自感电压由于电压电流为同一线圈上的, 只要参考方向确定了,其数学描述便可容易地写出,可不用 考虑线圈绕向。对线性电感,用u,i描述其特性,当u,i取关联 方向时,符号为正;当u,i为非关联方向时,符号为负
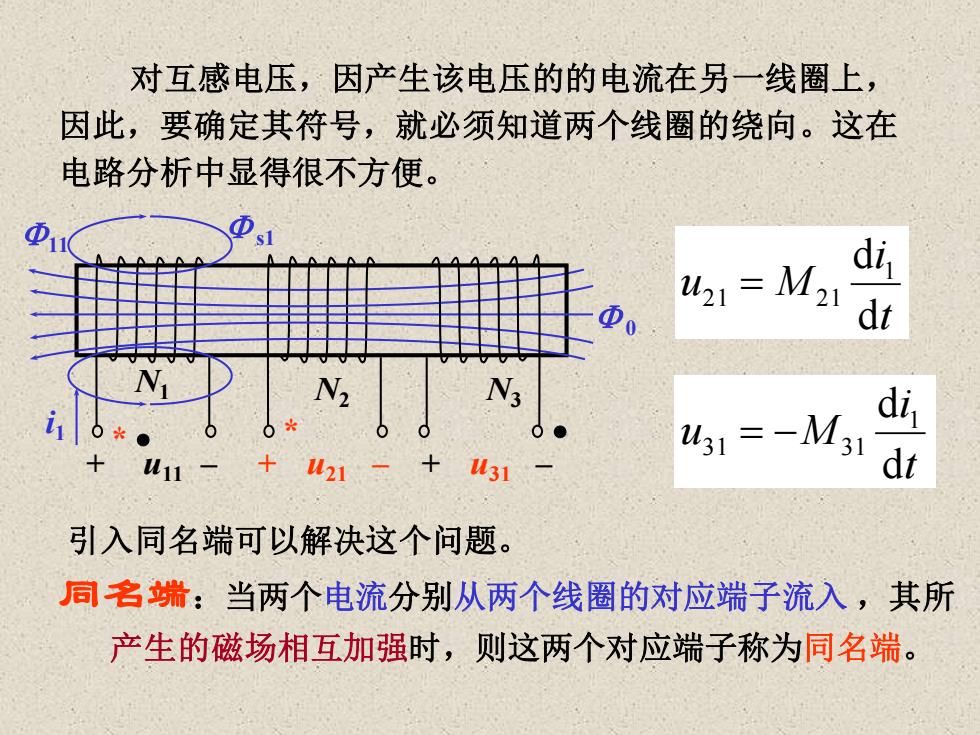
对互感电压,因产生该电压的的电流在另一线圈上, 因此,要确定其符号,就必须知道两个线圈的绕向。这在 电路分析中显得很不方便。 421=M21 di dr 431=-M31 di 421 u31 dt 引入同名端可以解决这个问题。 同名端:当两个电流分别从两个线圈的对应端子流入,其所 产生的磁场相互加强时,则这两个对应端子称为同名端
对互感电压,因产生该电压的的电流在另一线圈上, 因此,要确定其符号,就必须知道两个线圈的绕向。这在 电路分析中显得很不方便。 + u11 – + u21 – i1 11 0 N1 N2 + u31 – N3 s1 t i u M d d 1 21 = 21 引入同名端可以解决这个问题。 同名端:当两个电流分别从两个线圈的对应端子流入 ,其所 产生的磁场相互加强时,则这两个对应端子称为同名端。 * • * • t i u M d d 1 31 = − 31
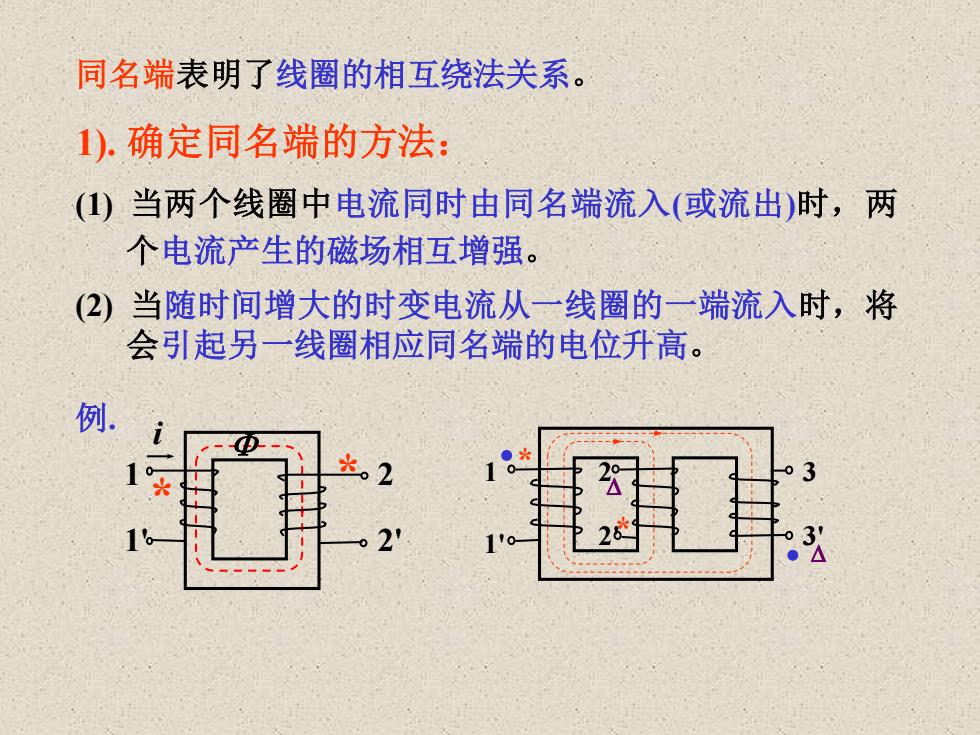
同名端表明了线圈的相互绕法关系。 1).确定同名端的方法: ()当两个线圈中电流同时由同名端流入(或流出)时,两 个电流产生的磁场相互增强。 (②)当随时间增大的时变电流从一线圈的一端流入时,将 会引起另一线圈相应同名端的电位升高。 例。 必。2 2 3
同名端表明了线圈的相互绕法关系。 1). 确定同名端的方法: (1) 当两个线圈中电流同时由同名端流入(或流出)时,两 个电流产生的磁场相互增强。 (2) 当随时间增大的时变电流从一线圈的一端流入时,将 会引起另一线圈相应同名端的电位升高。 i 1 1' 2 2' * * 1 1' 2 2' 3' 3 * * • • 例
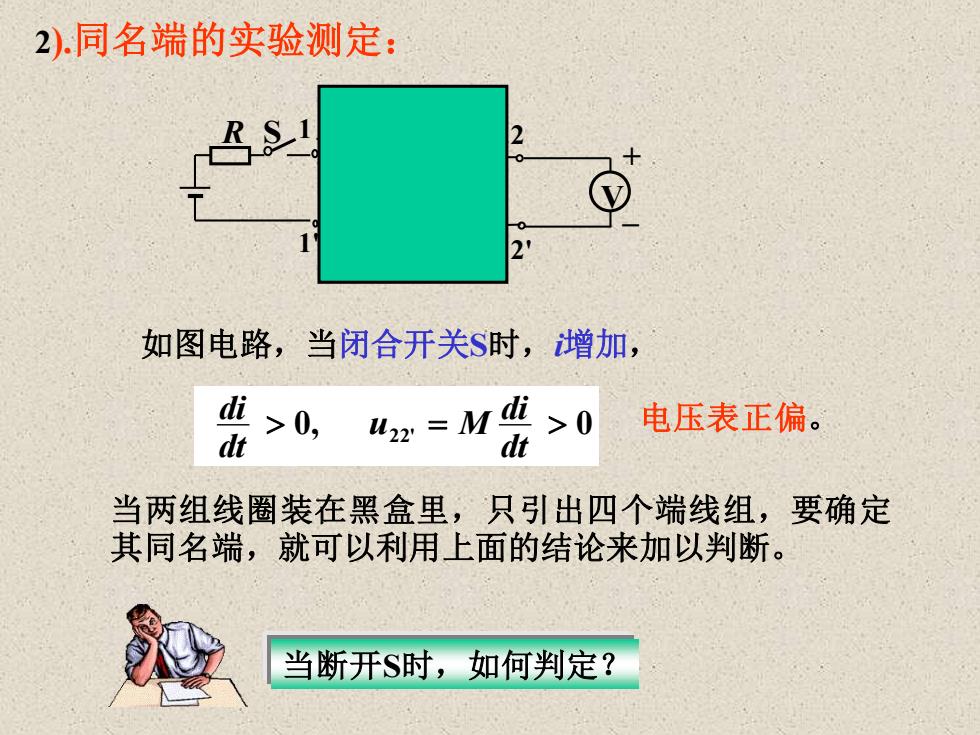
2)同名端的实验测定: 如图电路,当闭合开关$时,增加, 盟>0 4x=M出 >0 电压表正偏。 当两组线圈装在黑盒里,只引出四个端线组,要确定 其同名端,就可以利用上面的结论来加以判断。 当断开$时,如何判定?
2).同名端的实验测定: i 1 1' 2 2' * * R S V + – 0, 2 2' = 0 电压表正偏。 dt M di u dt di 如图电路,当闭合开关S时,i增加, 当两组线圈装在黑盒里,只引出四个端线组,要确定 其同名端,就可以利用上面的结论来加以判断。 当断开S时,如何判定?
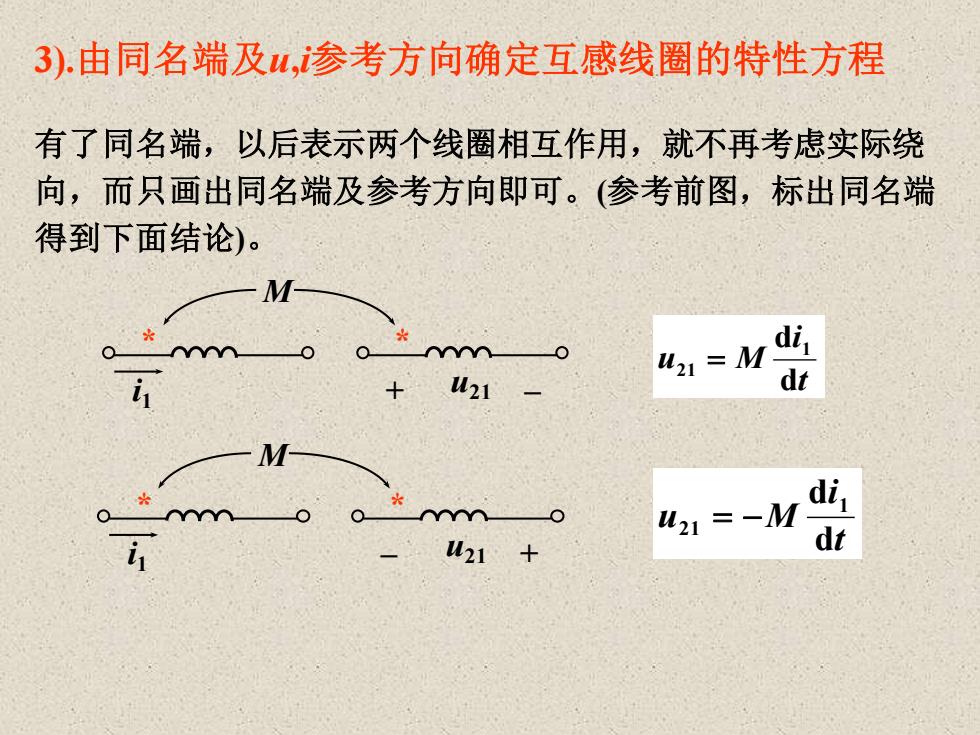
3).由同名端及山,参考方向确定互感线圈的特性方程 有了同名端,以后表示两个线圈相互作用,就不再考虑实际绕 向,而只画出同名端及参考方向即可。(参考前图,标出同名端 得到下面结论)。 M- *m0 41=M i 21 dt m 421=-M di, dt
3).由同名端及u,i参考方向确定互感线圈的特性方程 有了同名端,以后表示两个线圈相互作用,就不再考虑实际绕 向,而只画出同名端及参考方向即可。(参考前图,标出同名端 得到下面结论)。 t i u M d d 1 21 = t i u M d d 1 21 = − i1 * * + u21 – M i1 * * – u21 + M