
第二章控制系统的数学模型*2.1引言2.2系统的微分方程2.3传递函数2.4结构图X2.5信号流图?2.6 小结X
第二章 控制系统的数学模型 ❖ 2.1 引言 ❖ 2.2 系统的微分方程 ❖ 2.3 传递函数 ❖ 2.4 结构图 ❖ 2.5 信号流图 ❖ 2.6 小结
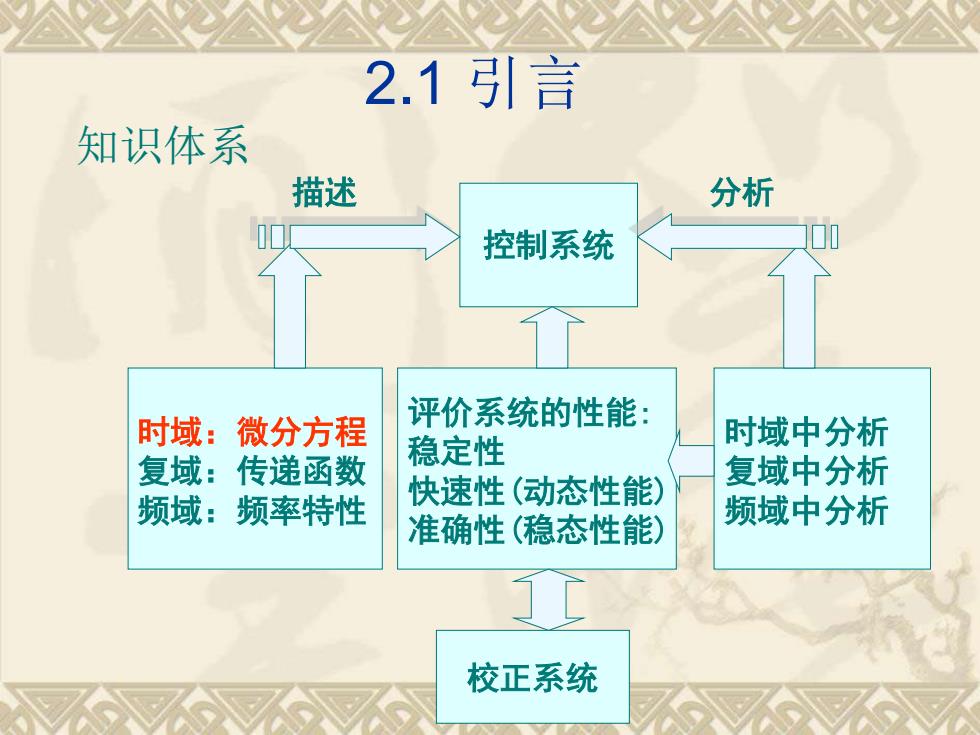
2.1引言知识体系描述分析控制系统评价系统的性能:时域:微分方程时域中分析稳定性复域:“传递函数复域中分析快速性(动态性能)频域:频率特性频域中分析准确性(稳态性能)校正系统
控制系统 时域:微分方程 复域:传递函数 频域:频率特性 2.1 引言 知识体系 描述 分析 时域中分析 复域中分析 频域中分析 评价系统的性能: 稳定性 快速性(动态性能) 准确性(稳态性能) 校正系统

2.1引言数学模型:描述系统各变量之间相互关系的数学表达式微分方程与时域模型:以时间为自变量,描述各变量的大8小以及各变量的变化趋势(变量的导数)之间关系最基本的数学工具就是微分方程。这种在时间域上建立的数学关系称为时域模型。复频域模型:对于线性定常系统,可以利用拉普拉斯变换和傅里叶变换,将时域模型转换为复频域模型。、本章重点:建立控制系统的微分方程模型传递函数模型结构图模型以及信号流图模型
2.1 引言 ❖ 数学模型:描述系统各变量之间相互关系的数学表达式. ❖ 微分方程与时域模型:以时间为自变量,描述各变量的大 小以及各变量的变化趋势(变量的导数)之间关系最基本 的数学工具就是微分方程。这种在时间域上建立的数学关 系称为时域模型。 ❖ 复频域模型:对于线性定常系统,可以利用拉普拉斯变换 和傅里叶变换,将时域模型转换为复频域模型。 ❖ 本章重点: 建立控制系统的微分方程模型 传递函数模型 结构图模型以及信号流图模型
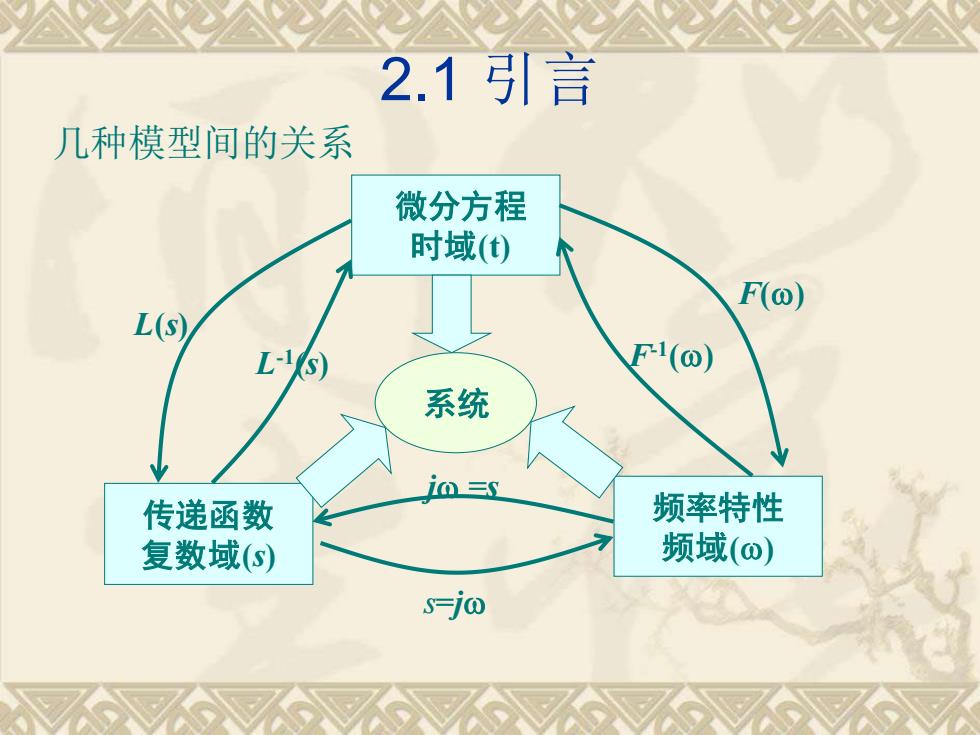
2.1引言几种模型间的关系微分方程时域(t)F(o)L(s)Fl()L-/s)系统inES频率特性传递函数频域(の)复数域(s)s-o
2.1 引言 几种模型间的关系 微分方程 时域(t) 传递函数 复数域(s) 频率特性 频域() L(s) L -1 (s) F() F-1 () s=j j =s 系统

2.2 系统的微分方程线性定常系统为本书主要研究的系统线性系统:满足线性叠加原理直观地看:系统输入值与输出值的函数波形不变化。线性叠加原理输入激励:u(t),u2(t),对应输出响应:yi(t),y2(t)有:若输入cu;(t)+βuz(t),则输出响应:ayi(t)+y2(t)本节要点:线性元件的微分方程,非线性微分方程的线性化,线性系统微分方程的编写
2.2 系统的微分方程 ❖ 线性定常系统为本书主要研究的系统。 ❖ 线性系统:满足线性叠加原理。 ●直观地看:系统输入值与输出值的函数波形不 变化。 ❖ 本节要点:线性元件的微分方程,非线性微 分方程的线性化,线性系统微分方程的编写 线性叠加原理 输入激励:u1 (t), u2 (t), 对应输出响应:y1 (t), y2 (t) 有:若输入u1 (t) + u2 (t), 则输出响应:y1 (t) + y2 (t)