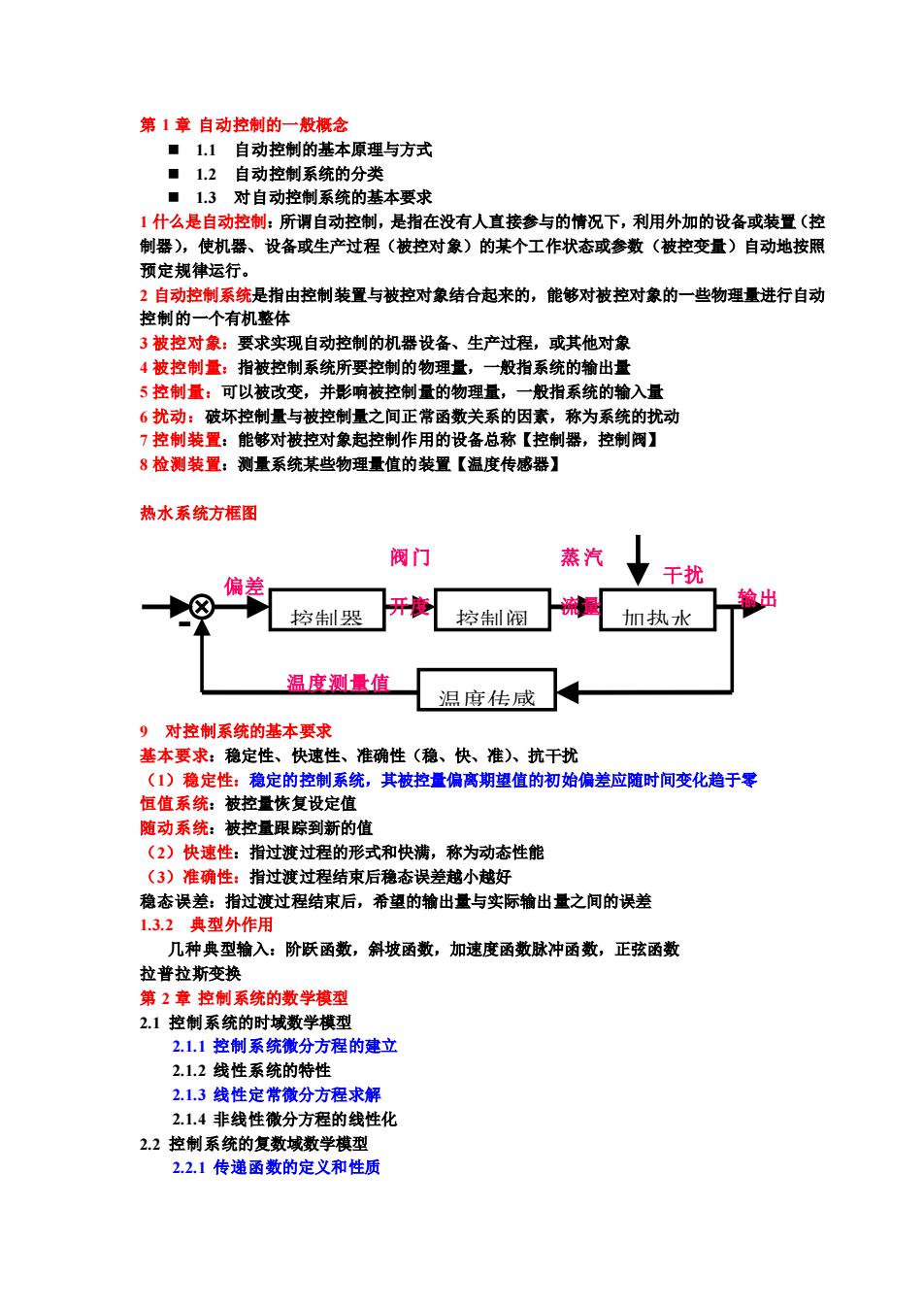
第1章自动控制的一般概念■1.1自动控制的基本原理与方式■1.2自动控制系统的分类■1.3对自动控制系统的基本要求1什么是自动控制:所调自动控制,是指在没有人直接参与的情况下,利用外加的设备或装置(控制器),使机器、设备或生产过程(被控对象)的某个工作状态或参数(被控变量)自动地按照预定规律运行。2自动控制系统是指由控制装置与被控对象结合起来的,能够对被控对象的一些物理量进行自动控制的一个有机整体3被控对象:要求实现自动控制的机器设备、生产过程,或其他对象4被控制量:指被控制系统所要控制的物理量,一般指系统的输出量5控制量:可以被改变,并影响被控制量的物理量,一般指系统的输入量6扰动:破坏控制量与被控制量之间正常函数关系的因素,称为系统的扰动7控制装置:能够对被控对象起控制作用的设备总称【控制器,控制阀】8检测装置:测量系统某些物理量值的装置【温度传感器】热水系统方框图阀门蒸汽0干扰偏差输出X开度流量控制器控制阀加执水温度测量值温度传咸9对控制系统的基本要求基本要求:稳定性、快速性、准确性(稳、快、准)、抗干扰(1)稳定性:稳定的控制系统,其被控量偏离期望值的初始偏差应随时间变化趋于零恒值系统:被控量恢复设定值随动系统:被控量跟踪到新的值(2)快速性:指过渡过程的形式和快满,称为动态性能(3)准确性:指过渡过程结束后稳态误差越小越好稳态误差:指过渡过程结束后,希望的输出量与实际输出量之间的误差1.3.2典型外作用几种典型输入:阶跃函数,斜坡函数,加速度函数脉冲函数,正弦函数拉普拉斯变换第2章控制系统的数学模型2.1控制系统的时域数学模型2.1.1控制系统微分方程的建立2.1.2线性系统的特性2.1.3线性定常微分方程求解2.1.4非线性微分方程的线性化2.2控制系统的复数域数学模型2.2.1传递函数的定义和性质
第 1 章 自动控制的一般概念 ◼ 1.1 自动控制的基本原理与方式 ◼ 1.2 自动控制系统的分类 ◼ 1.3 对自动控制系统的基本要求 1 什么是自动控制:所谓自动控制,是指在没有人直接参与的情况下,利用外加的设备或装置(控 制器),使机器、设备或生产过程(被控对象)的某个工作状态或参数(被控变量)自动地按照 预定规律运行。 2 自动控制系统是指由控制装置与被控对象结合起来的,能够对被控对象的一些物理量进行自动 控制的一个有机整体 3 被控对象:要求实现自动控制的机器设备、生产过程,或其他对象 4 被控制量:指被控制系统所要控制的物理量,一般指系统的输出量 5 控制量:可以被改变,并影响被控制量的物理量,一般指系统的输入量 6 扰动:破坏控制量与被控制量之间正常函数关系的因素,称为系统的扰动 7 控制装置:能够对被控对象起控制作用的设备总称【控制器,控制阀】 8 检测装置:测量系统某些物理量值的装置【温度传感器】 热水系统方框图 9 对控制系统的基本要求 基本要求:稳定性、快速性、准确性(稳、快、准)、抗干扰 (1)稳定性:稳定的控制系统,其被控量偏离期望值的初始偏差应随时间变化趋于零 恒值系统:被控量恢复设定值 随动系统:被控量跟踪到新的值 (2)快速性:指过渡过程的形式和快满,称为动态性能 (3)准确性:指过渡过程结束后稳态误差越小越好 稳态误差:指过渡过程结束后,希望的输出量与实际输出量之间的误差 1.3.2 典型外作用 几种典型输入:阶跃函数,斜坡函数,加速度函数脉冲函数,正弦函数 拉普拉斯变换 第 2 章 控制系统的数学模型 2.1 控制系统的时域数学模型 2.1.1 控制系统微分方程的建立 2.1.2 线性系统的特性 2.1.3 线性定常微分方程求解 2.1.4 非线性微分方程的线性化 2.2 控制系统的复数域数学模型 2.2.1 传递函数的定义和性质 控制器 控制阀 加热水 箱 温度传感 器 输出 温度测量值 蒸 汽 流量 偏差 阀门 开度 干扰

2.2.2传递函数的零点和极点2.2.3典型环节的传递函数2.3控制系统的结构图2.3.1结构图的基本元素2.3.2几个基本概念及术语2.3.3结构图的绘制2.3.4结构图的简化2.4信号流图与梅森增益公式2.4.1信号流图的组成及性质2.4.2信号流图的绘制2.4.3梅森增益公式第3章线性系统的时域分析法3.1系统时间响应的性能指标3.1.1动态过程与稳态过程3.1.2动态性能与稳态性能3.2一阶系统的时域分析3.2.1一阶系统的数学模型3.2.2单位阶跃响应3.2.3单位脉冲响应3.2.4单位斜坡响应3.2.5单位加速度响应3.3二阶系统的时域分析3.3.1二阶系统的数学模型3.3.2单位阶跃响应3.3.3欠阻尼二阶系统动态过程分析3.3.4过阻尼二阶系统动态过程分析3.3.5单位斜坡响应3.3.6二阶系统性能的改善3.5线性系统的稳定性分析3.5.1稳定的基本概念3.5.2线性系统稳定的充要条件3.5.3劳斯一赫尔维茨稳定判据3.6线性系统的稳态误差3.6.1误差与稳态误差3.6.2系统类型3.6.3阶联输入作用下的稳态误差3.6.4斜坡输入作用下的稳态误差3.6.5加速度输入作用下的稳态误差3.6.6扰动作用下的稳态误差3.6.7减小或消除稳态误差的措施第4章线性系统的根轨迹法4.1根轨迹法的基本概念根轨迹:开环系统某一参数从零变化到无穷时,闭环系统特征方程的根在平面上变化的轨迹理解:
2.2.2 传递函数的零点和极点 2.2.3 典型环节的传递函数 2.3 控制系统的结构图 2.3.1 结构图的基本元素 2.3.2 几个基本概念及术语 2.3.3 结构图的绘制 2.3.4 结构图的简化 2.4 信号流图与梅森增益公式 2.4.1 信号流图的组成及性质 2.4.2 信号流图的绘制 2.4.3 梅森增益公式 第 3 章 线性系统的时域分析法 3.1 系统时间响应的性能指标 3.1.1 动态过程与稳态过程 3.1.2 动态性能与稳态性能 3.2 一阶系统的时域分析 3.2.1 一阶系统的数学模型 3.2.2 单位阶跃响应 3.2.3 单位脉冲响应 3.2.4 单位斜坡响应 3.2.5 单位加速度响应 3.3 二阶系统的时域分析 3.3.1 二阶系统的数学模型 3.3.2 单位阶跃响应 3.3.3 欠阻尼二阶系统动态过程分析 3.3.4 过阻尼二阶系统动态过程分析 3.3.5 单位斜坡响应 3.3.6 二阶系统性能的改善 3.5 线性系统的稳定性分析 3.5.1 稳定的基本概念 3.5.2 线性系统稳定的充要条件 3.5.3 劳斯—赫尔维茨稳定判据 3.6 线性系统的稳态误差 3.6.1 误差与稳态误差 3.6.2 系统类型 3.6.3 阶跃输入作用下的稳态误差 3.6.4 斜坡输入作用下的稳态误差 3.6.5 加速度输入作用下的稳态误差 3.6.6 扰动作用下的稳态误差 3.6.7 减小或消除稳态误差的措施 第 4 章 线性系统的根轨迹法 4.1 根轨迹法的基本概念 根轨迹:开环系统某一参数从零变化到无穷时,闭环系统特征方程的根在平面上变化的轨迹 理解:

2■根轨迹是闭环特征根的轨迹(s-z.)闭环特征根就是闭环系统的极点K*j=I■闭环系统的极点决定了系统的稳定性等性质-1■有参数变化,特征方程的根相当于某个参数的函数(s- p,)4.1.2根轨迹方程i=1Is- p, I1KI(s- p)IIs-z, Ii=lj=1根轨迹就是当K*变化时,系统所有闭环极点的集合,也就是当K*变化时,满足根轨迹方程的所有解的集合。相角条件是绘制根轨迹的充分必要条件■要确定一个测试点是否在根轨迹上,只需要看其否满足相角条件■确定根轨迹上某一点的K*值时,才使用模值条件Z(s-p)=(2k+1)元,LCS-k =0.±1±2...i=li=l4.2根轨迹的绘制4.3广义根轨迹4.3.1参数根轨迹4.3.2附加开环零点的作用:作用1:改变稳定性;作用2:改善动态性能4.3.3零度根轨迹第5章线性系统的频域分析法5.1频率特性什么叫频率特性?2一个稳定的线性系统,当输入正弦信号时,则输出信号是与输入同频率、但幅值和相位(一般)不同的正弦信号。三种模型的关系频率特性曲线:1、幅相频率特性曲线奈奎斯特(Nyquist)曲线,或极坐标图2、对数频率特性曲线伯德(Bode)图K3、对数幅相特性曲线尼柯尔斯(Nichols)图G(jo) ~5.2典型环节的频率特性(jo)"5.2.4开环幅相曲线的绘制(1)确定在=0+和处的点K元在低频段,即起点处Aca02lim β(jの) =-(n-m)×90°即幅相曲线终于坐标原点终止角0>α(2)确定与实轴的交点,即Q()=0
◼ 根轨迹是闭环特征根的轨迹 ◼ 闭环特征根就是闭环系统的极点 ◼ 闭环系统的极点决定了系统的稳定性等性质 ◼ 有参数变化,特征方程的根相当于某个参数的函数 4.1.2 根轨迹方程 根轨迹就是当 K*变化时,系统所有闭环极点的集合,也就是当 K*变化时,满足根轨迹方程的所 有解的集合。 ◼ 相角条件是绘制根轨迹的充分必要条件 ◼ 要确定一个测试点是否在根轨迹上,只需要看其否满足相角条件 ◼ 确定根轨迹上某一点的 K*值时,才使用模值条件 4.2 根轨迹的绘制 4.3 广义根轨迹 4.3.1 参数根轨迹 4.3.2 附加开环零点的作用:作用 1:改变稳定性;作用 2:改善动态性能 4.3.3 零度根轨迹 第 5 章 线性系统的频域分析法 5.1 频率特性 什么叫频率特性?一个稳定的线性系统,当输入正弦信号时,则输出信号是与输入同频率、但幅 值和相位(一般)不同的正弦信号。 三种模型的关系 频率特性曲线: 1、幅相频率特性曲线——奈奎斯特(Nyquist)曲线,或极坐标图 2、对数频率特性曲线——伯德(Bode)图 3、对数幅相特性曲线——尼柯尔斯(Nichols)图 5.2 典型环节的频率特性 5.2.4 开环幅相曲线的绘制 (1)确定在ω=0+和∞处的点 在低频段,即起点处 即幅相曲线终于坐标原点 ;终止角 (2)确定与实轴的交点,即 Q(ω)=0 1 ( ) ( ) 1 * 1 = − − − = = n i i m j j s p s z K ( ) ( ) (2 1) , 0, 1, 2 1 1 − − − = + = = = s z s p k k n i i m j j 1 ( ) ( ) 1 * 1 = − − = = n i i m j j s p s z K = = − − = m j j n i i s z s p K 1 * 1 | | | | v j K G j ( ) ( ) 2 ( ) , ( ) v K A v = = − lim ( ) = −( − )90 → j n m

5.2.5开环对数频率特性曲线的绘制幅频特性 A()=A(o)L(0)= 20lg A(0)N-2201g 4(o)=24(o)i=li=l系统幅频特性是各环节幅频特性的叠加N相频特性 (の)=,()i=l系统相频特性是各环节相频特性的叠加84绘制幅频特性曲线的步骤1)开环传函按典型环节分解2)确定各环节交接频率3)绘制低频段渐近线K在低频段G(jo)~(jo)"低频段曲线斜率为-20vdB/dec确定低频渐近线上的一点在の<0min取点0。=0.01,0.1,1L.(o)=20lgK-20vlg004)做の>min频率段的渐近线86根据频率特性曲线确定系统传递函数,仅适用于最小相位系统5.3频率域稳定判据
5.2.5 开环对数频率特性曲线的绘制 84 = = = = = N i i N i Ai L L A 1 1 20lg ( ) ( ) ( ) 20lg ( ) = = N i A Ai 1 () () = = N i i 1 () () 系统幅频特性是各环节幅频特性的叠加 系统相频特性是各环节相频特性的叠加 幅频特性 相频特性 绘制幅频特性曲线的步骤 1)开环传函按典型环节分解 2)确定各环节交接频率 3)绘制低频段渐近线 86 在低频段 v j K G j ( ) ( ) 低频段曲线斜率为 -20v dB/dec 确定低频渐近线上的一点 在 min 取点 0 = 0.01, 0.1, 1 0 0 La ( ) = 20lg K − 20v lg 4)做 min 频率段的渐近线 根据频率特性曲线确定系统传递函数,仅适用于最小相位系统 5.3 频率域稳定判据

幅角原理:设s平面闭合曲线包围F(s)的Z个零点和P个极点,当s沿r顺时针运动一周时,在F(s)平面上,对应的闭合曲线包围原点的圈数DAR-r包围零点个数T包围原点圈数T包围极点个数R<0顺时针R>0逆时针R=0不包围1141、Nyquist稳定判据奈氏判据:反馈控制系统稳定的充分必要条件是半闭合曲线TGH不穿过(-1,jO)点,且逆时针包围临界点(-1,jO)的圈数R等于开环传递函数的正实部极点数P由幅角原理知R=P-ZP为G(s)H(s)正实部极点个数,R为TGH逆时针包围(-1,jo)的圈数F(s)的零点即是闭环稳定,则Z=0闭环极点Z=P-R=P-2N=0 P=R1242.对数频率稳定判据P为开环正实部极点数,系统稳定的充分必要条件是:p(0)±(2k+1)元L(0)>0且T穿越(2k+1)π的次数N=N,-N满足Z=P-R=P-2N=0型次v>0的系统,需要在相频起始段向上补做v×90°的虚直线。补做虚直线的穿越皆为负穿越141
114 幅角原理:设s平面闭合曲线Γ包围F(s)的Z个零 点和P个极点,当s沿Γ顺时针运动一周时,在F(s) 平面上,对应的闭合曲线ΓF包围原点的圈数 R = P − Z R 0 顺时针 R 0 逆时针 R = 0 不包围 Γ包围零点个数 Γ包围极点个数 ΓF包围原点圈数 1、Nyquist 稳定判据 124 奈氏判据:反馈控制系统稳定的充分必要条件是半 闭合曲线ΓGH不穿过(-1,j0)点,且逆时针包围临界点 (-1,j0)的圈数R等于开环传递函数的正实部极点数P 由幅角原理知 P为G(s)H(s)正实部极点个数,R 为ΓGH逆时针包 围(-1,j0)的圈数 R = P − Z 闭环稳定,则 Z = 0 F(s)的零点即是 闭环极点 Z = P − R = P − 2N = 0 P = R 141 2. 对数频率稳定判据 P为开环正实部极点数,系统稳定的充分必要条件 是: L() 0 Z = P − R = P − 2N = 0 且Γφ穿越(2k+1)π的次数N=N+ -N-满足 (c ) (2k +1) 型次v>0的系统,需要在相频起始段向上补做 v90 的虚直线。补做虚直线的穿越皆为负穿越