
2.2系统的微分方程列写物理系统的微分方程步骤(1)定义系统及其组成元件,确定各元件的输入量和输出量确定系统的输入量、中间变量和输出量(2)确定必要的假设条件(3)根据系统自身的物理规律列写各组成元件的原始方程(4)消去中间变量建立系统描述输出量与输入量之间关系的微分方程(5)若是线性方程,方程左右两边导数项按降幂排列输出量有关各项=》方程左边d'xdx如:m+kr=F输入量有关各项=》方程右边十dtdt?若为非线性方程,线性化处理
2.2 系统的微分方程 ❖ 列写物理系统的微分方程步骤: (1)定义系统及其组成元件,确定各元件的输入量和输出量, 确定系统的输入量、中间变量和输出量。 (2)确定必要的假设条件。 (3)根据系统自身的物理规律列写各组成元件的原始方程。 (4)消去中间变量建立系统描述输出量与输入量之间关系的 微分方程。 (5)若是线性方程,方程左右两边导数项按降幂排列 输出量有关各项=〉方程左边 输入量有关各项=〉方程右边 若为非线性方程,线性化处理。 kx F dt dx f dt d x m + + = 2 2 如 :
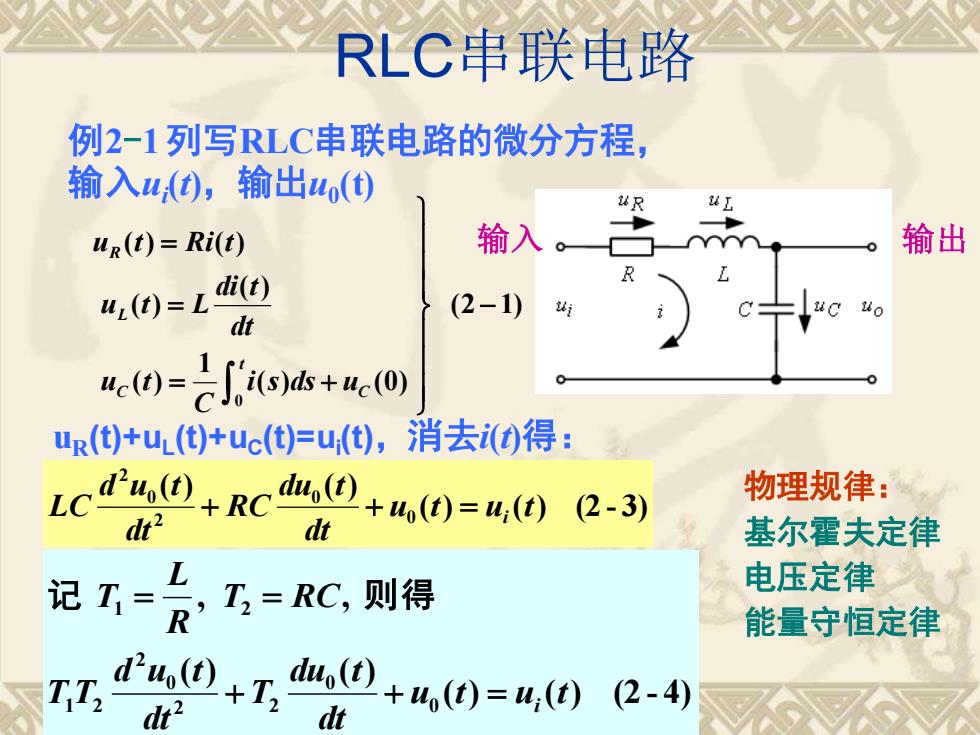
RLC串联电路例2-1列写RLC串联电路的微分方程输入u(t),输出uo(t)URUL输出输入ur(t) = Ri(t)一ZRdi(t)ur(t)= L(2-1)uiuC&1dtuc(t)=J'i(s)ds + uc(0)our(t)+uL(t)+uc(t)=u(t),消去i(t)得:物理规律:d'u,(t)duo(t)LC+RC+uo(t)=u;(t) (2-3)dt?dt基尔霍夫定律1电压定律记T,=RC,则得TR能量守恒定律d'uo(t)du,(t)T,T,+T,+uo(t)=u,(t)(2-4)dt2dt
输入 输出 ( ) ( ) (2 - 3) ( ) ( ) 0 0 2 0 2 u t u t dt du t RC dt d u t LC + + = i ( ) ( ) (2 - 4) ( ) ( ) , , 0 0 2 2 0 2 1 2 1 2 u t u t dt du t T dt d u t T T T RC R L T + + = i 记 = = 则 得 例2-1 列写RLC串联电路的微分方程, 输入ui (t),输出u0 (t) uR(t)+uL (t)+uC(t)=ui (t),消去i(t)得: RLC串联电路 物理规律: 基尔霍夫定律 电压定律 能量守恒定律 (2 1) ( ) (0) 1 ( ) ( ) ( ) ( ) ( ) 0 − = + = = C t C L R i s ds u C u t dt di t u t L u t Ri t

弹簧-质量-阻尼器系统例2-2列写如图所示弹簧aty3质量、阻尼器系统的微分方程,输入F(t),输出y(t)。黏性摩擦β物理规律:牛顿第二定理mFum(所有外力之和=ma=mi=miFC假设壁摩擦为黏性摩擦,摩擦力为β[dy(t)/dtl,β为黏性系数;弹簧力为ky(t),k为弹性系数。d'y(t)dy(t)F(t)-B-ky(t)(2-5)mdt?dtd'y(t)dy(t)+β+ ky(t) = F(t)(2-6)mdt?dt
弹簧-质量-阻尼器系统 例2-2 列写如图所示弹簧、 质量、阻尼器系统的微分方 程,输入F(t) ,输出 y(t)。 物理规律:牛顿第二定理 ( ) (2 - 5) ( ) ( ) ( ) 2 2 ky t dt dy t F t β dt d y t m = − − ( ) ( ) (2 - 6) ( ) ( ) 2 2 ky t F t dt dy t β dt d y t m + + = F ma mv my sum (所有外力之和) = = = 假设壁摩擦为黏性摩擦,摩擦力为[dy(t)/dt],为黏性系 数;弹簧力为ky(t),k为弹性系数

机械转动系统例2-3考虑右图的机械传动系统,输入为外加转矩M(t),输出为转角t)物理规律:转动系统牛顿定律负载的转M(所有外力矩之和动惯量=Jα=Jo=Jed'°0(t)do(t)0Mβy(t)M-输出输入dt?dtYβ黏性阻扭转弹1e(t)de(t)2即:性系数尼系数+βy(t) = M(t)(2-7)+1dt?dt
( ) ( ) ( ) 2 2 t dt d t M dt d t J = − − 负载的转 动惯量 黏性阻 尼系数 扭转弹 性系数 输出 输入 机械转动系统 例2-3 考虑右图的机械传动 系统,输入为外加转矩 M(t) ,输出为转角(t)。 ( ) ( ) (2 - 7) ( ) ( ) : 2 2 t M t dt d t dt d t J + + = 即 物理规律:转动系统牛顿定律 J J J Msum = = = (所有外力矩之和)
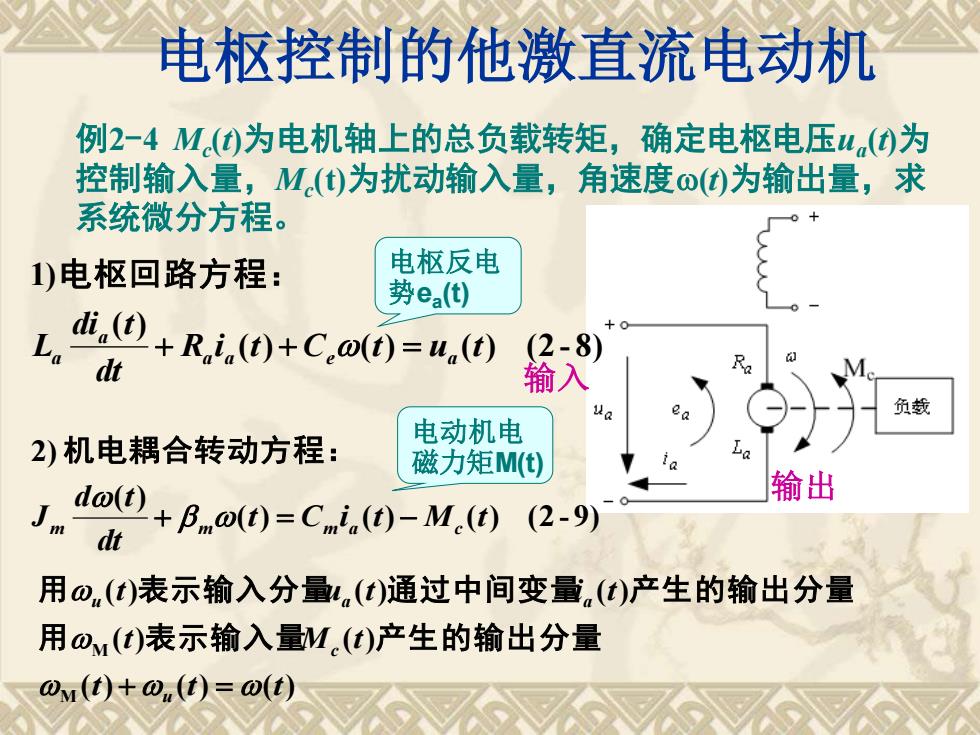
电枢控制的他激直流电动机例2-4M(t)为电机轴上的总负载转矩,确定电枢电压u(t)为控制输入量,M(t)为扰动输入量,角速度の(t)为输出量,求系统微分方程。电枢反电1)电枢回路方程:势ea(t)di.(t)+0(2-8)+R.i.(t)+C.o(t)=u.(t)aR.dt输入负裁ua-电动机电2)机电耦合转动方程:Lo磁力矩M(t)输出do(t)βmo(t)=Cmi.(t)-M.(t)(2-9)mdt用の(t)表示输入分量u(t)通过中间变量(t)产生的输出分量用の(t)表示输入量M(t)产生的输出分量W(t) +0, (t) = w(t)
输入 输出 电枢控制的他激直流电动机 ( ) ( ) ( ) (2 - 8) ( ) 1) R i t C t u t dt di t L a a e a a a + + = 电枢回路方程: ( ) ( ) ( ) (2 - 9) ( ) 2) t C i t M t dt d t Jm + m = m a − c 机电耦合转动方程: 例2-4 Mc (t)为电机轴上的总负载转矩,确定电枢电压ua (t)为 控制输入量,Mc (t)为扰动输入量,角速度(t)为输出量,求 系统微分方程。 电枢反电 势ea (t) 电动机电 磁力矩M(t) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) M M t t t t M t t u t i t u c u a a + = 用 表示输入量 产生的输出分量 用 表示输入分量 通过中间变量 产生的输出分量