
第一章:1闭环系统(或反馈系统)的特征:采用负反馈,系统的被控变量对控制作用有直接影响,即被控变量对自已有控制作用。2典型闭环系统的功能框图。自动控制在没有人直接参与的情况下,通过控制器使被控对象或过程按照预定的规律运行。自动控制系统由控制器和被控对象组成,能够实现自动控制任务的系统。被控制量在控制系统中:按规定的任务需要加以控制的物理量。控制量作为被控制量的控制指令而加给系统的输入星:也称控制输入。扰动量干扰或破坏系统按预定规律运行的输入量,也称扰动输入或干扰入。反馈通过测量变换装置将系统或元件的输出量反送到输入端,与输入信号相比较。反送到输入端的信号称为反馈信号。负反馈反馈信号与输人信号相减,其差为偏差信号。负反馈控制原理检测偏差用以消除偏差。将系统的输出信号引回插入端,与输入信号相减,形成偏差信号。然后根据偏差信号产生相应的控制作用,力图消除或减少偏差的过程。开环控制系统,系统的输入和输出之间不存在反馈回路,输出量对系统的控制作用没有影响,这样的系统称为开环控制系统。开环控制义分为无扰动补偿和有扰动补偿两种。闭环控制系统凡是系统输出端与输入端存在反馈回路,即输出量对控制作用有直接影响的系统,叫作闭环控制系统。自动控制原理课程中所讨论的主要是闭环负反馈控制系统。复合控制系统复合控制系统是一种将开环控制和闭环控制结合在一起的控制系统。它在闭环控制的基础上,用开环方式提供一个控制输入信号或扰动输入信号的顺馈通道,用以提高系统的精度。自动控制系统组成闭环负反馈控制系统的典型结构如图1.2所示。组成一个自动控制系统通常包括以下基本元件1.给定元件给出与被控制量希望位相对应的控制输入信号(给定信号),这个控制输入信号的量纲要与主反馈信号的量纲相同。给定元件通常不在闭环回路中。2.测量元件测量元件也叫传感器,用于测量被控制量,产生与被控制量有一定函数关系的信号。被控制量成比例或与其导数成比例的球信号。测量元件的精度直接影响控制系统的精度被控对象被控制盘给定元件丝制量一9±既择—做大元件]执行元件上应使测量元件的精度高于系统的精度,还要有足够宽的频带。3.比较无件用于比较控制量和反反债校(局部反馈)反馈量正元件馈量并产生偏差信号。电桥、运算放大器可作为测量元件(主反馈)电信号的比较元件。有些比较元件与测量元件是结合在一起的,如测角位移的旋转变压器和自整角机等。4.放大元件对信号进行幅值或功率的图1.2典型负反馈控制系统结构放大,以及信号形式的变换。如交流变直流的相敏整流或直流变交流的相敏调制。5.执行元件用于操纵被控对象,如机械位移系统中的电动机、液压伺服马达、温度控制系统中的加热装置。执行元件的选择应具有足够大的功率和足够宽的频带。6.校正元件用于改善系统的动态和稳态性能。根据被控对象特点和性能指标的要求而设计。校正元件串联在由偏差信号到被控制信号间的前向通道中的称为串联校正:校正元件在反馈回路中的称为反馈校正。7。被控对象控制系统所要控制的对象,例如水箱水位控制系统中的水箱、房间温度控制系统中的房间、火炮随动系统中的火炮、电动机转速控制系统中电机所带的负载等。设计控制系统时,认为被控对象是不可改变的,它的输出即为控制系统的被控制量。8.能源元件为控制系统提供能源的元件,在方框图中通常不画出。对控制系统的基本要求1.稳定性稳定性是系统正常工作的必要条件。2.准确性要求过渡过程结束后,系统的稳态精度比较高,稳态误差比较小.或者对某种典型输入信号的稳态误差为零。3。快速性系统的响应速度快、过渡过程时间短、超调量小。系统的稳定性足够好、频带足够宽,才可能实现快速性的要求。第二章:1、建立系统的微分方程。2、绘制动态框图并求传递函数。3、传递函数在零初始条件下,系统输出量的拉氏变换与输入量的拉氏变换之比称为传递函数。传递函数的概念适用于线性定常单输入、单输出系统。求传递函数通常有两种方法:对系统的微分方程取拉氏变换,或化简系统的动态方框图。对于由电阻、电感、电容元件组成的电气网络,一般采用运算阻抗的方法求传递函数。4、结构图的变换与化简化简方框图是求传递函数的常用方法。对方框图进行变换和化简时要遵循等效原则:对任一环节进行变换时,变换前后该环节的输人量、输出量及其相互关系应保持不变。化简方框图的主要方法就是将串联环节、并联环节和基本反馈环节用一个等效环节代替。化简方框图的关键是解除交叉结1Z0(s)A(s)构,即移动分支点或相加点,使被简化的环节中不存在与外部直接相连的分支点和相加点。5、H(s)=六A利用梅森(Mason)公式求传递函数。O(s)第i条前向通路传递函数的乘积。△流图的特征式=1-所有回路传递函数乘积之和+每两个互不接触回路传递函数乘积之和-每三个...=1-L。+L,LA,余子式,从A中处除去与第条前向通路接触的回路be第三章:1、一阶系统对典型输入信号的输出响应。(单位)阶跃函数(Stepfunction)1(t),t≥0;(单位)斜坡函数(Ramp
= i i i H s Q (s) (s) 1 ( ) 第一章:1 闭环系统(或反馈系统)的特征:采用负反馈,系统的被控变量对控制作用有直接影响,即被控变量对自己有控 制作用 。2 典型闭环系统的功能框图。 自动控制 在没有人直接参与的情况下,通过控制器使被控对象或过程按照预定的规律运行。 自动控制系统 由控制器和被控对象组成,能够实现自动控制任务的系统。 被控制量 在控制系统中.按规定的任务需要加以控制的物理量。 控制量 作为被控制量的控制指令而加给系统的输入星.也称控制输入。 扰动量 干扰或破坏系统按预定规律运行的输入量,也称扰动输入或干扰掐入。 反馈 通过测量变换装置将系统或元件的输出量反送到输入端,与输入信号相比较。反送到输入端的信号称为反馈信号。 负反馈 反馈信号与输人信号相减,其差为偏差信号。 负反馈控制原理 检测偏差用以消除偏差。将系统的输出信号引回插入端,与输入信号相减,形成偏差信号。然后根据偏差 信号产生相应的控制作用,力图消除或减少偏差的过程。 开环控制系统 系统的输入和输出之间不存在反馈回路,输出量对系统的控制作用没有影响,这样的系统称为开环控制系统。 开环控制又分为无扰动补偿和有扰动补偿两种。 闭环控制系统 凡是系统输出端与输入端存在反馈回路,即输出量对控制作用有直接影响的系统,叫作闭环控制系统。 自动控制原理课程中所讨论的主要是闭环负反馈控制系统。 复合控制系统 复合控制系统是一种将开环控制和闭环控制结合在一起的控制系统。它在闭环控制的基础上,用开环方式提 供一个控制输入信号或扰动输入信号的顺馈通道,用以提高系统的精度。 自动控制系统组成 闭环负反馈控制系统的典型结构如图 1.2 所示。组成一个自动控制系统通常包括以下基本元件 1.给定元件 给出与被控制量希望位相对应的控制输入信号(给定信号),这个控制输入信号的量纲要与主反馈信号的量纲相 同。给定元件通常不在闭环回路中。2.测量元件 测量元件也叫传感器,用于测量被控制量,产生与被控制量有一定函数关 系的信号。被控制量成比例或与其导数成比例的 信号。测量元件的精度直接影响控制系统的精度 应使测量元件的精度高于系统的精度,还要有足 够宽的频带。3.比较无件 用于比较控制量和反 馈量并产生偏差信号。电桥、运算放大器可作为 电信号的比较元件。有些比较元件与测量元件是 结合在一起的,如测角位移的旋转变压器和自整 角机等。4.放大元件 对信号进行幅值或功率的 放大,以及信号形式的变换.如交流变直流的相敏整流或直流变交流的相敏调制。5.执行元件 用于操纵被控对象,如机械 位移系统中的电动机、液压伺服马达、温度控制系统中的加热装置。执行元件的选择应具有足够大的功率和足够宽的频带。 6.校正元件 用于改善系统的动态和稳态性能。根据被控对象特点和性能指标的要求而设计。校正元件串联在由偏差信号到 被控制信号间的前向通道中的称为串联校正;校正元件在反馈回路中的称为反馈校正。7.被控对象 控制系统所要控制的对 象,例如水箱水位控制系统中的水箱、房间温度控制系统中的房间、火炮随动系统中的火炮、电动机转速控制系统中电机所 带的负载等。设计控制系统时,认为被控对象是不可改变的,它的输出即为控制系统的被控制量。8.能源元件 为控制系统 提供能源的元件,在方框图中通常不画出。 对控制系统的基本要求 1.稳定性 稳定性是系统正常工作的必要条件。2.准确性 要求过渡过程结束后,系统的稳态精度比 较高,稳态误差比较小.或者对某种典型输入信号的稳态误差为零。3.快速性 系统的响应速度快、过渡过程时间短、超调 量小。系统的稳定性足够好、频带足够宽,才可能实现快速性的要求。 第二章:1、建立系统的微分方程。2、绘制动态框图并求传递函数。3、传递函数 在零初始条件下,系统输出量的拉氏变换 与输入量的拉氏变换之比称为传递函数。传递函数的概念适用于线性定常单输入、单输出系统。求传递函数通常有两种方法: 对系统的微分方程取拉氏变换,或化简系统的动态方框图。对于由电阻、电感、电容元件组成的电气网络,一般采用运算阻 抗的方法求传递函数。4、结构图的变换与化简 化简方框图是求传递函数的常用方法。对方框图进行变换和化简时要遵循等 效原则:对任一环节进行变换时,变换前后该环节的输人量、输出量及其相互关系应保持不变。化简方框图的主要方法就是 将串联环节、并联环节和基本反馈环节用一个等效环节代替。化简方框图的关键是解除交叉结 构,即移动分支点或相加点,使被简化的环节中不存在与外部直接相连的分支点和相加点。5、 利用梅森(Mason)公式求传递函数。 Q (s) i 第 i 条前向通路传递函数的乘积。 流图的特征式= 1 - 所有回路传递函数乘积之和+每两个互不接触回路传递函数乘 积之和-每三个.=1- + − b c b c a La L L . i余子式,从中处除去与第i条前向通路接触的回路 第三章:1、一阶系统对典型输入信号的输出响应。(单位)阶跃函数(Step function)1(t) , t 0 ;(单位)斜坡函数(Ramp
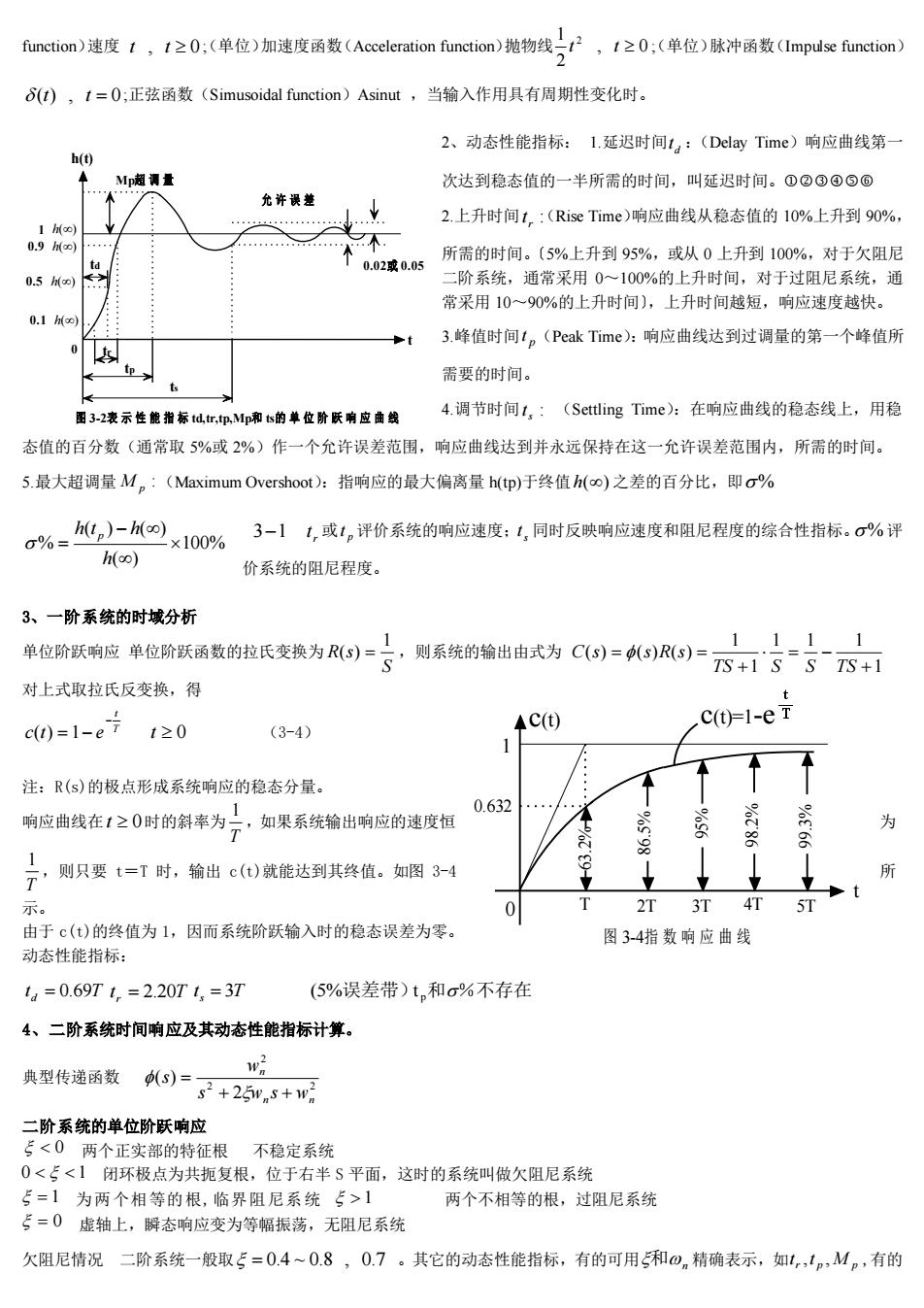
function)速度t,t≥O;(单位)加速度函数(Accelerationfunction)抛物线t≥0;(单位)脉冲函数(Impulsefunction)2S(t),t=O;正弦函数(Simusoidalfunction)Asinut,当输入作用具有周期性变化时。2、动态性能指标:1.延迟时间ta:(DelayTime)响应曲线第一h(t)Mp超调量次达到稳态值的一半所需的时间,叫延迟时间。①②?③③允许误差2.上升时间t:(RiseTime)响应曲线从稳态值的10%上升到90%,1 h(o0)..0.9 h(c0)A所需的时间。(5%上升到95%,或从0上升到100%,对于欠阻尼0.02或0.05-二阶系统,通常采用0~100%的上升时间,对于过阻尼系统,通0.5 h(oo)常采用10~90%的上升时间),上升时间越短,响应速度越快。0.1 h(3.峰值时间tp(PeakTime):响应曲线达到过调量的第一个峰值所t需要的时间。4.调节时间t,:(SettlingTime):在响应曲线的稳态线上,用稳图3-2表示性能指标td,tr,tp,Mp和ts的单位阶跃响应曲线态值的百分数(通常取5%或2%)作一个允许误差范围,响应曲线达到并永远保持在这一允许误差范围内,所需的时间。5.最大超调量M。:(MaximumOvershoot):指响应的最大偏离量h(tp)于终值h(o)之差的百分比,即α%h(t,) -h(0)3-1t,或t,评价系统的响应速度;t,同时反映响应速度和阻尼程度的综合性指标。α%评0%=x100%h(o0)价系统的阻尼程度。3、一阶系统的时域分析11111单位阶跃响应单位阶跃函数的拉氏变换为R(s)则系统的输出由式为C(s)=Φ(s)R(s)=STS+1 S STS+1对上式取拉氏反变换,得t.C(t)=1-e T1^C(t)c(t)=1-e 7t≥0(3-4)-注:R(s)的极点形成系统响应的稳态分量。0.63200%S6%S为响应曲线在t≥0时的斜率为,如果系统输出响应的速度恒-T89261E9+1+所,则只要t=T时,输出c(t)就能达到其终值。如图3-4★★A++tT2T3T4T05T示。由于c(t)的终值为1,因而系统阶跃输入时的稳态误差为零。图3-4指数响应曲线动态性能指标:ta=0.69Tt,=2.20T t,=3T(5%误差带)t.和α%不存在4、二阶系统时间响应及其动态性能指标计算。wa典型传递函数(s) =s*+25w,s+wm二阶系统的单位阶跃响应<0两个正实部的特征根不稳定系统0<<1闭环极点为共复根,位于右半S平面,这时的系统叫做欠阻尼系统5=1为两个相等的根,临界阻尼系统>1两个不相等的根,过阻尼系统=0虚轴上,瞬态响应变为等幅振荡,无阻尼系统欠阻尼情况二阶系统一般取==0.4~0.8,0.7。其它的动态性能指标,有的可用和の,精确表示,如t,,tp,M,,有的
0 t Mp超 调 量 允 许 误 差 1 0.9 0.5 0.1 tr tp ts 图 3-2表 示 性 能 指 标 td,tr,tp,Mp和 ts的 单 位 阶 跃 响 应 曲 线 td h(t) 0.02或 0.05 h() h() h() h() 100% ( ) ( ) ( ) % − = h h t p h 图 3-4指 数 响 应 曲 线 1 0 63.2% 86.5% 95% 98.2% 99.3% T 2T 3T 4T 5T 0.632 t c(t) c(t)=1-e 2 2 2 2 ( ) n n n s w s w w s + + = 0 0 1 = 1 1 = 0 function)速度 t , t 0 (单位)加速度函数( ; Acceleration function)抛物线 , 0 2 1 2 t t (单位)脉冲函数( ; Impulse function) (t) , t = 0 ;正弦函数(Simusoidal function)Asinut ,当输入作用具有周期性变化时。 2、动态性能指标: 1.延迟时间 d t :(Delay Time)响应曲线第一 次达到稳态值的一半所需的时间,叫延迟时间。 2.上升时间 : r t (Rise Time)响应曲线从稳态值的 10%上升到 90%, 所需的时间。〔5%上升到 95%,或从 0 上升到 100%,对于欠阻尼 二阶系统,通常采用 0~100%的上升时间,对于过阻尼系统,通 常采用 10~90%的上升时间〕,上升时间越短,响应速度越快。 3.峰值时间 p t (Peak Time):响应曲线达到过调量的第一个峰值所 需要的时间。 4.调节时间 : s t (Settling Time):在响应曲线的稳态线上,用稳 态值的百分数(通常取 5%或 2%)作一个允许误差范围,响应曲线达到并永远保持在这一允许误差范围内,所需的时间。 5.最大超调量 : M p (Maximum Overshoot):指响应的最大偏离量 h(tp)于终值 h() 之差的百分比,即 % 3−1 r t 或 p t 评价系统的响应速度; s t 同时反映响应速度和阻尼程度的综合性指标。 % 评 价系统的阻尼程度。 3、一阶系统的时域分析 单位阶跃响应 单位阶跃函数的拉氏变换为 S R s 1 ( ) = ,则系统的输出由式为 1 1 1 1 1 1 ( ) ( ) ( ) + = − + = = TS S S TS C s s R s 对上式取拉氏反变换,得 T t c t e − ( ) = 1− t 0 (3-4) 注:R(s)的极点形成系统响应的稳态分量。 响应曲线在 t 0 时的斜率为 T 1 ,如果系统输出响应的速度恒 为 T 1 ,则只要 t=T 时,输出 c(t)就能达到其终值。如图 3-4 所 示。 由于 c(t)的终值为 1,因而系统阶跃输入时的稳态误差为零。 动态性能指标: t d = 0.69T t r = 2.20T t s = 3T (5%误差带)t p和%不存在 4、二阶系统时间响应及其动态性能指标计算。 典型传递函数 二阶系统的单位阶跃响应 两个正实部的特征根 不稳定系统 闭环极点为共扼复根,位于右半 S 平面,这时的系统叫做欠阻尼系统 为两个相等的根,临界阻尼系统 两个不相等的根,过阻尼系统 虚轴上,瞬态响应变为等幅振荡,无阻尼系统 欠阻尼情况 二阶系统一般取 = 0.4 ~ 0.8 , 0.7 。其它的动态性能指标,有的可用和n 精确表示,如 r p M p t ,t , ,有的

很难用和の,准确表示,如ta,t,,可采用近似算法。当0<<1时,特征根Vi-=2S1.2=-5w,±jw,/1-g2-,wa=w.V1-90 = arctanA1+0.6§ +0.2g2td0<5<1ta1+0.75On(1)时,亦可用tOn(2)t,(上升时间),=-βOd一定,即β一定,→の。个→t,响应速度越快5(3)t,(峰值时间)元tp=Od一定时,の,个(闭环极点力负实轴的距离越远)→t,(4)%orM,的计算,超调量超调量在峰值时间发生,故h(t)即为最大输出Eh(t,)-h(c0)×100%=e /-s×100%0%=h(0)(5)调节时间1s的计算选取误差带3.53.5=0.05ts≤tsSonFOn4.54.5△=0.02ts≤ts =50nEon3(△= 0.05)ts =Son当较小5≤0.44(A = 0.02)ts =Eon系统的单位阶跃响应为1e-5 sin(wat +0)C(t)=1-Vi-52动态性能指标计算公式为
n d t 2 1+ 0.6 + 0.2 t d = 0 1 很难用 和n 准确表示,如 d s t ,t ,可采用近似算法。当 0 1 时,特征根 s1.2= 2 −wn jwn 1− , 2 2 , 1 1 arctan = − − = wd wn 时,亦可用 n d t 1+ 0.7 ⑴ = ⑵ r t (上升时间) d r t − = 一定,即 一定, →n →t r ,响应速度越快 ⑶ (峰值时间) p t d p t = 一定时,n (闭环极点力负实轴的距离越远)→t p ⑷ % or M p的计算,超调量 超调量在峰值时间发生,故 ( ) p h t 即为最大输出 100% 100% ( ) ( ) ( ) % 2 1 = − = − − e h h t p h ⑸调节时间 S t 的计算 选取误差带 n S n S t t 3.5 3.5 = 0.05 = n S n S t t 4.5 4.5 = 0.02 = 当 较小 0.4 ( 0.02) 4 ( 0.05) 3 = = = = n S n S t t 系统的单位阶跃响应为 C(t)=1- sin( ) 1 1 2 + − − e w t d w t n 动态性能指标计算公式为

元-01, =Z-0_上升时间WaW,V1-52元-0=-一1峰值时间T2WaWyi-g?12元其中Ta是有阻尼振荡周期,且Ta-Ja是有阻尼振荡频率。faWaJ1-×100%超调量,=e3_04(△=0.02)(=0.05)或t,=调整时间ts=5WnSwnN=号1.5V1-53-1.5振荡次数(△=0.05)n,元5Ta72/1-52-2N=1_2或(△=0.02)Ta元5Ing,5、系统稳定性分析特征根必须全部分布在S平面的左半部,即具有负实部。已知系统的特征方程时,可采用Routh稳定判据或Hurwitz稳定判据判定系统的稳定性。特征多项式各项系数均大于零(或同符号)是系统稳定的必要条件。Routh判据:由特征方程各项系数列出Routh表,如果表中第一列各项严格为正,则系统稳定:第一列出现负数,则系统不稳定,且第一列各项数值符号改变的次数就是正实部特征根的数目。Hurwitz判据:由特征方程各项系数构成的各阶Hurwitz行列式全部为正,则系统稳定。劳斯稳定判据是根据所列劳斯表第一列系数符号的变化,去判别特征方程式根在S平面上的具体分布,过程如下:①如果劳斯表中第一列的系数均为正值,则其特征方程式的根都在S的左半平面,相应的系统是稳定的。②如果劳斯表中第一列系数的符号有变化,其变化的次数等于该特征方程式的根在S的右半平面上的个数,相应的系统为不稳定。在应用劳斯判据时,有可能会碰到以下两种特殊情况,·劳斯表某一行中的第一项等于零,而该行的其余各项不等于零或没有余项,这种情况的出现使劳斯表无法继续往下排列。解决的办法是以一个很小的正数6来代替为零的这项,据此算出其余的各项,完成劳斯表的排列。·劳斯表中出现全零行则表示相应方程中含有一些大小相等符号相反的实根或共轭虚根。这种情况,可利用系数全为零行的上一行系数构造一个辅助多项式,并以这个辅助多项式导数的系数来代替表中系数为全零的行。完成劳斯表的排列。6、稳态误差的计算KII(t,s+1)i=l令系统开环传递函数为G(s)H(s)=n≥m1-1sII(T,s+1)j=l[v=00型系统I型系统V:为系统中含有的积分环节数v=1(v=2II型系统V>2时,II型以上的系统,实际上很难使之稳定,所以这种类型的系统在控制工程中一般不会碰到。(复合系统)
上升时间 2 1 − − = − = n d r w w t 峰值时间 d n d p T w w t 2 1 1 2 = − − = = 其中 Td 是有阻尼振荡周期,且 Td= d d d f f w , 1 2 = 是有阻尼振荡频率。 超调量 100% 2 1 = − − e p 调整时间 ( 0.02) 4 ( 0.05) 3 = = = = n s n s w t w t 或 振荡次数 N= d p s T t ln 1.5 1 1.5 2 − = − = ( =0.05) 或 N= d p s T t ln 2 1 2 2 − = − = ( =0.02) 5、系统稳定性分析 特征根必须全部分布在 S 平面的左半部,即具有负实部。已知系统的特征方程时,可采用 Routh 稳定判据或 Hurwitz 稳定判 据判定系统的稳定性。特征多项式各项系数均大于零(或同符号)是系统稳定的必要条件。 Routh 判据:由特征方程各项系数列出 Routh 表,如果表中第一列各项严格为正,则系统稳定;第一列出现负数,则系统不 稳定,且第一列各项数值符号改变的次数就是正实部特征根的数目。 Hurwitz 判据:由特征方程各项系数构成的各阶 Hurwitz 行列式全部为正,则系统稳定。劳斯稳定判据是根据所列劳斯表第 一列系数符号的变化,去判别特征方程式根在 S 平面上的具体分布,过程如下: ① 如果劳斯表中第一列的系数均为正值,则其特征方程式的根都在 S 的左半平面,相应的系统是稳定的。 ② 如果劳斯表中第一列系数的符号有变化,其变化的次数等于该特征方程式的根在 S 的右半平面上的个数,相应的系统为 不稳定。 在应用劳斯判据时,有可能会碰到以下两种特殊情况。 ·劳斯表某一行中的第一项等于零,而该行的其余各项不等于零或没有余项,这种情况的出现使劳斯表无法继续往下排列。 解决的办法是以一个很小的正数 来代替为零的这项,据此算出其余的各项,完成劳斯表的排列。 ·劳斯表中出现全零行 则表示相应方程中含有一些大小相等符号相反的实根或共轭虚根。这种情况,可利用系数全为零行的上一行系数构造一个辅 助多项式,并以这个辅助多项式导数的系数来代替表中系数为全零的行。完成劳斯表的排列。 6、稳态误差的计算 令系统开环传递函数为 n m s T s K s G s H s j n j i m i + + = − = = , ( 1) ( 1) ( ) ( ) 1 1 ( ) 2 2 1 0 0 : 系统在控制工程中一般不会碰到。复合系统 时, 型以上的系统,实际上很难使之稳定,所以这种类型的 型系统 型系统 型系统 为系统中含有的积分环节数 = = =
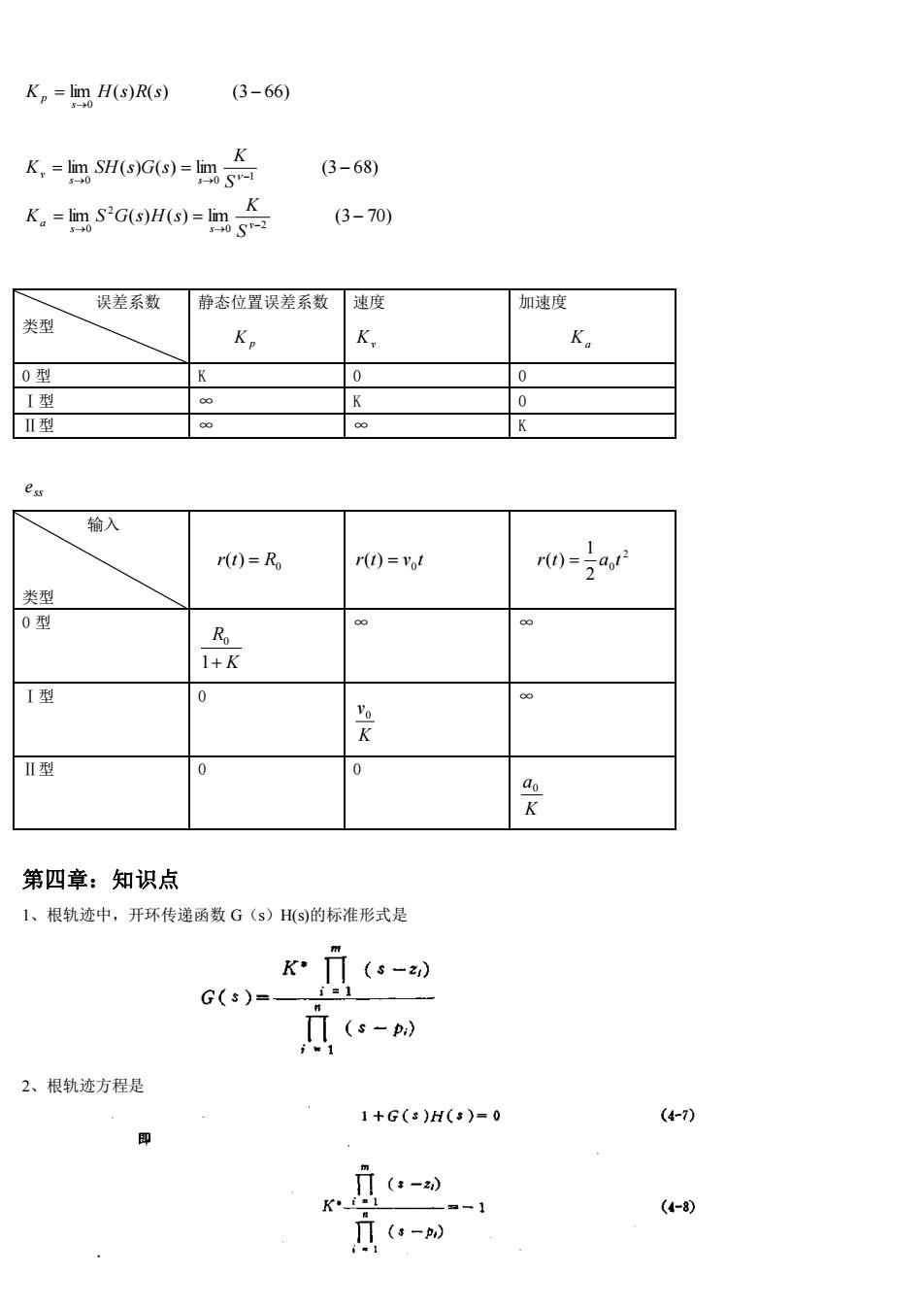
K, = lim H(s)R(s)(3- 66)s>(K(3-68)K, = lim SH(s)G(s) = lim5-0 5V-15→0KK, = lim S°G(s)H(s) = lim(3 70)5-0 5r-2误差系数静态位置误差系数速度加速度类型K,K,K.0型K00I型K08ⅡI型8K8ess输入11a1?r(t)= Ror(t)=Votr(t)=-2类型0型88Ro1+ KI型08VoKⅡ型00aoK第四章:知识点1、根轨迹中,开环传递函数G(s)H(s)的标准形式是K*(s -z)i=1G(s)=n(s-p)#2、根轨迹方程是(4-7)1+G(s)H(s)=0即(s-2)Ki.(4-8)(s -p)
lim ( ) ( ) (3 66) 0 = − → K H s R s s p lim ( ) ( ) lim (3 68) 1 0 0 = = − → → − S K K SH s G s s s v lim ( ) ( ) lim (3 70) 2 0 2 0 = = − → → v− s s a S K K S G s H s 误差系数 类型 静态位置误差系数 K p 速度 Kv 加速度 Ka 0 型 K 0 0 Ⅰ型 ∞ K 0 Ⅱ型 ∞ ∞ K ss e 输入 类型 0 r(t) = R r t v t 0 ( ) = 2 0 2 1 r(t) = a t 0 型 K R 1+ 0 ∞ ∞ Ⅰ型 0 K v0 ∞ Ⅱ型 0 0 K a0 第四章:知识点 1、根轨迹中,开环传递函数 G(s)H(s)的标准形式是 2、根轨迹方程是 .