
1考试方式闭卷笔试制卷份数4、闭环系统特征方程为1+三0:其根轨迹在实轴上的分离点为(s(s+4)三共题号二四五大tD.-1.414A.-1.577B、-0.423C.-2得分)5、对于一阶、二阶系统来说,系统特征方程式的所有系数都是正数是系统稳定的(Y2(A、充分条件,B、必要条件,C、充分必要条件,D、以上都不是闵卷人核分人页第三,判断题(你认为下列命题是否正确,对正确的就在题干前的括号内打~,错误的打"x,每小一、填空题(每空1分,共10分)题2分,共10分)-1、典型二阶报荡环节,当0<5<0.707时,诺报频率e_与自热频率e。的关系是贝、1型系统极标图的奈氏曲线的起点是在相角为0的无限远处,2、反馈控制系统是根据给定值和的偏差进行调节的控制系统:>2、滞后一超前校正装置奈氏图的形状为一个圆3、对自动控制系统的基本要求是)3、二阶系统的阻尼比《在大于1的蔗时,阶跃响应曲线为非周期过程。4、负反馈根轨起始于)4、某线性离敢系统其特征方程为D(2)-2-2+1,则其稳定,5、当开环增益一定时,采样周期越采样系统稳定性越)5、在伯德图中反映系统动态特性的是中频段。6、申联校正装置可分为超前校正、潜后校正和7、理想继电特性的捕述函数是四、简答题:(每小题5分,共20分)1、描述函数:二、单项选舞题(从下列各题四个备选答案中选出一个正确答案,并将其代号写在题干前面的括号内。答案选错或未选者,该题不得分。每小题2分,共10分)2、偶极子:)1、设开环系统的频率特性G(j)当=1rad/s时,其频率特性幅值M1)为3、焦点:(1+ jo)4、传递雨数:AIBCD、2S)2、某单位反馈系统开环传雨为若使其成为二阶最佳模型,则a值为s(s+a)五、计算题(每小题10分,共20分)AV2B.2V2C(S)C、2D、V2/2(每种方法5分)1)系统方框图如下,用两种方法求出传递数R(S)K(α+1))3、单位负反馈系统的开环传递函数为:G(s)=则困环系统稳定的条件是:s*(Ts+I)A、只要K很小,B、只要K很大,C, T>t, D、Tt
共 2 页 第 1 页 考试方式 闭卷笔试 制卷份数 ( )4、闭环系统特征方程为 0 ( 4) 1 = + + s s K ,其根轨迹在实轴上的分离点为 A、-1.577 B、-0.423 C、-2 D、-1.414 ( )5、对于一阶、二阶系统来说,系统特征方程式的所有系数都是正数是系统稳定的( )。 A、充分条件, B、必要条件,C、充分必要条件, D、 以上都不是 三、判断题(你认为下列命题是否正确,对正确的就在题干前的括号内打“√”,错误的打“×”,每小 题 2 分,共 10 分) ( )1、Ⅰ型系统极坐标图的奈氏曲线的起点是在相角为0的无限远处。 ( )2、滞后—超前校正装置奈氏图的形状为一个圆。 ( )3、二阶系统的阻尼比ξ在大于 1 的范围时,阶跃响应曲线为非周期过程。 ( )4、某线性离散系统其特征方程为 D(z)=Z2-Z+1,则其稳定。 ( )5、在伯德图中反映系统动态特性的是中频段。 四、简答题:(每小题 5 分,共 20 分) 1、描述函数: 2、偶极子: 3、焦点: 4、传递函数: 五、计算题(每小题 10 分,共 20 分) 1) 系统方框图如下,用两种方法求出传递函数 R(S) C(S) 。(每种方法 5 分) 题号 一 二 三 四 五 六 七 得分 阅卷人 核分人 一、填空题(每空 1 分,共 10 分) 1、典型二阶振荡环节,当 0< <0.707 时,谐振频率 m 与自然频率 n 的关系是 ; 2、反馈控制系统是根据给定值和_的偏差进行调节的控制系统; 3、对自动控制系统的基本要求是 、 、 ; 4、负反馈根轨迹起始于 ; 5、当开环增益一定时,采样周期越 ,采样系统稳定性越 ; 6、串联校正装置可分为超前校正、滞后校正和_; 7、理想继电特性的描述函数是 ; 二、单项选择题(从下列各题四个备选答案中选出一个正确答案,并将其代号写在题干前面的括 号内。答案选错或未选者,该题不得分。每小题 2 分,共 10 分) ( )1、设开环系统的频率特性 G(jω)= 2 (1 j ) 1 + ,当ω=1rad/s 时,其频率特性幅值 M(1)为 A、1 B、 2 C、 2 1 D、 4 1 ( )2、某单位反馈系统开环传函为 ( ) 1 s s + a 若使其成为二阶最佳模型,则 a 值为 A、 2 B、 2 2 C、2 D、 2 / 2 ( )3、单位负反馈系统的开环传递函数为: ( 1) ( 1) ( ) 2 + + = s Ts K s G s ,则闭环系统稳定的条件是: A、只要 K 很小 , B、只要 K 很大, C、T>τ, D、 T<τ
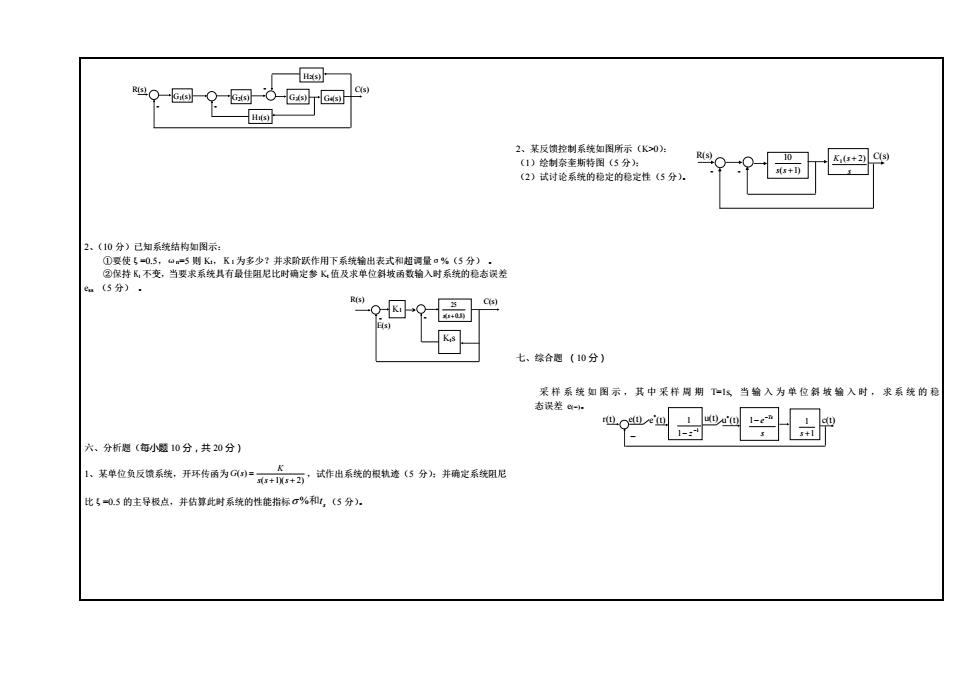
C(sRILCGi(s)G(s)GsGe(s)Hi(s)2、某反馈控制系统如图所示(K>0):R(s)Cs(1)绘制奈奎斯特图(5分):s(s+1)(2)试讨论系统的稳定的稳定性(5分).2、(10分)已知系统结构如图示:①要使5=0.5,a=5则Kt,K:为多少?并求阶跃作用下系统输出表式和超调量α%(5分)②保持K,不变,当要求系统其有最佳阻尼比时确定参K值及求单位斜坡函数输入时系统的稳态误差ea(5分):R(s)C(s)O-KHEs七、综合题(10分)采样系统如图示,其中采样周期T-Is当输入为单位斜坡输入时,求系统的稳态误差e-ro)e(n)u(t)'(t)eft1:~六、分析题(每小题10分,共20分)K1、某单位负反馈系统,开环传函为G(s)=,试作出系统的根轨连(5分):并确定系统阻尼s(s+1(s+2)比5=0.5的主导极点,并估算此时系统的性能指标G%和,(5分)
2、(10 分)已知系统结构如图示: ①要使ξ=0.5,ωn=5 则 Kt,K1 为多少?并求阶跃作用下系统输出表式和超调量σ%(5 分) 。 ②保持 K1 不变,当要求系统具有最佳阻尼比时确定参 Kt 值及求单位斜坡函数输入时系统的稳态误差 ess (5 分) 。 六、分析题(每小题 10 分,共 20 分) 1、某单位负反馈系统,开环传函为 ( 1)( 2) ( ) + + = s s s K G s ,试作出系统的根轨迹(5 分);并确定系统阻尼 比ξ=0.5 的主导极点,并估算此时系统的性能指标 s %和t (5 分)。 2、某反馈控制系统如图所示(K>0): (1)绘制奈奎斯特图(5 分); (2)试讨论系统的稳定的稳定性(5 分)。 七、综合题 (10 分) 采 样 系统如图示,其中 采 样 周 期 T=1s, 当 输 入 为 单 位 斜 坡 输 入 时 , 求 系 统 的 稳 态误差 e(∞)。 ( 0.8) 25 s s + Kts R(s) E(s) C(s) - - K1 1 1 1 − − z s e −Ts 1− 1 1 s + e(t) u(t) u * r(t) (t) c(t) _ e * (t) G1(s) G2(s) H1(s) G3(s) H2(s) G4(s) - - R(s) - C(s) s K (s 2) 1 + - - R(s) C(s) ( 1) 10 s s +