北京邮电大学出版社：21世纪高等学校规划教材《高等数学》课程教学资源（PPT课件讲稿）第5章 定积分 1定积分的概念

第5章 定积分 不定积分 积分学 定积分

第5章 定积分 积分学 不定积分 定积分

第1为 第五章 定积分的桡念 一、引例 二、 定积分定义 三、定积分的几何意义 BEIJING UNIVERSITY OF POSTS AND TELECOMMUNICATIONS PRESS 目录上页 下页 返回 结束

目录 上页 下页 返回 结束 第1节 一、引例 二、 定积分定义 三、 定积分的几何意义 定积分的概念 第五章

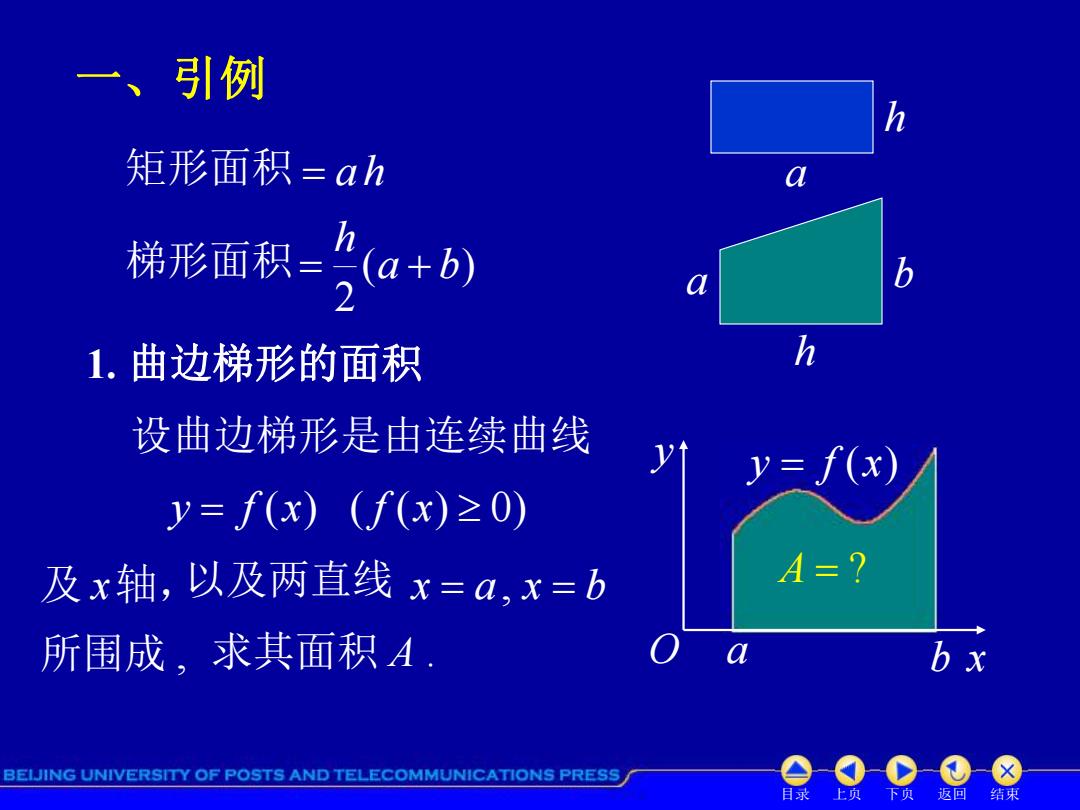
一、引例 矩形面积=ah 梯形面积-身a+) b 1.曲边梯形的面积 h 设曲边梯形是由连续曲线 y y=f(x) y=f(x)(f(x)≥0) 及x轴，以及两直线x=a,x=b A=? 所围成，求其面积A: a bx BEIJING UNIVERSITY OF POSTS AND TELECOMMUNICATIONS PRESS 目录 上负 下 返回 结束

目录 上页 下页 返回 结束 一、引例 1. 曲边梯形的面积 设曲边梯形是由连续曲线 y  f (x) ( f (x)  0) 及 x轴，以及两直线 x  a, x  b 所围成 , 求其面积 A . A  ? y  f (x) 矩形面积 a h  a h a h 梯形面积 ( ) b 2 a b h   y O a b x

解决步骤： 1)分割.在区间[a,b]中任意插入n-1个分点 a=x0<x<x2<<Xn-1<xn=b 用直线x=x,将曲边梯形分成个小曲边梯形： 2)近似代替.在第i个窄曲边梯形上任取5，∈[x-1,x] 作以[x1,x,]为底，f(5) 为高的小矩形。并以此小 矩形面积近似代替相应 窄曲边梯形面积△4，得 a xy Xi-1 xi bx 51 △4，≈f(5a)△x;(△x,=x1-xi-1,i=1,2,…,n) BEIJING UNIVERSITY OF POSTS AND TELECOMMUNICATIONS PRESS 目录 返回 结束

目录 上页 下页 返回 结束 1x i x i1 a x b x y O 解决步骤 : 1) 分割. 在区间 [a , b] 中任意插入 n –1 个分点 a x x x x x b  0  1  2  n1  n  [ , ] i i 1 i x x    用直线 i x  x 将曲边梯形分成 n 个小曲边梯形; 2) 近似代替. 在第i 个窄曲边梯形上任取 作以[ , ] i 1 i x x  为底 , ( ) i f  为高的小矩形, 并以此小 矩形面积近似代替相应 窄曲边梯形面积 , Ai 得 ( ) ( )  i  i  i  i  i  i1 A f  x x x x , i 1,2,,n )  i

3)求和. A=2A4,=2f5)△x i=1 i=1 4)取极限.令2=max{△x},则曲边梯形面积 1si≤n n A=lim∑A4, 2→0 1 lim∑f(5,)△x, 0 a O a x Xi-xi bx BEIJING UNIVERSITY OF POSTS AND TELECOMMUNICATIONS PRESS 目录 返回 结束

目录 上页 下页 返回 结束 3) 求和.     n i A Ai 1     n i i i f x 1 ( ) 4) 取极限. 令 max{ }, 1 i i n  x    则曲边梯形面积      n i A Ai 1 0 lim       n i i i f x 1 0 lim ( )  1x i x i1 a x b x y O  i