
例4已知 求(AB) 解法一 因为 所以 4r- 解法二 w-- 18
18 解法一 因为 = − − = 2 6 2 0 1 1 2 1 1 1 1 2 3 1 0 1 AB 所以 . = 0 6 2 2 (AB) 解法二 1 1 1 2 1 2 2 ( ) 0 2 . 1 1 1 0 6 1 3 − = = = − AB B A 例4 已知 1 1 1 0 1 , 2 1 , 1 2 3 1 1 − = = − A B 求 ( ) . AB

最后,还要特别指出,作为特殊矩阵的向量,它具有 矩阵的许多特征.比如,矩阵的加法、减法和数乘的运算 规则及其算律对向量都适用.设有四维行向量 a=(3,12,-1),B=(2,2,1,3), 则 a+p=(3+2,1+2,2+1,-1+3) =(5,3,3,2), a-B=(3-2,1-2,2-1,-1-3) =(1,-1,1,-4) 2a=(2×3,2×1,2×2,2×(-1) =(6,2,4,-2) 19
19 最后,还要特别指出,作为特殊矩阵的向量,它具有 矩阵的许多特征.比如,矩阵的加法、减法和数乘的运算 规则及其算律对向量都适用.设有四维行向量 , 则 α = (3,1,2,−1), β = (2,2,1,3) (5,3,3,2), (3 2,1 2,2 1, 1 3) = α +β = + + + − + (1, 1,1, 4), (3 2,1 2,2 1, 1 3) = − − α −β = − − − − − (6,2,4, 2). 2 (2 3,2 1,2 2,2 ( 1)) = − α = −

第三节几种特殊矩阵 设A=[a,]是n阶方阵,其中元素a,a2,,anm称为方阵A 的主对角元,它们的连线称为方阵A的主对角线: 一、单位矩阵 主对角线上的元素都是1,其余元素全是0的n阶方阵 [1 0… 0 0 1. 0 0 0. 称为”阶单位矩阵,记作E,在不致引起混乱时可简记为E. 易证,对任何矩阵Bm,恒有 E B=B,BE=B. 21
21 设 是 阶方阵,其中元素 称为方阵 的主对角元,它们的连线称为方阵 的主对角线. [ ] A = aij n A A a a ann , , , 11 22 一、单位矩阵 主对角线上的元素都是1,其余元素全是0的 阶方阵 称为 阶单位矩阵,记作 ,在不致引起混乱时可简记为 . n n 0 0 1 0 1 0 1 0 0 En E 易证,对任何矩阵 ,恒有 . Bmn Em B = B, BEn = B 第三节 几种特殊矩阵
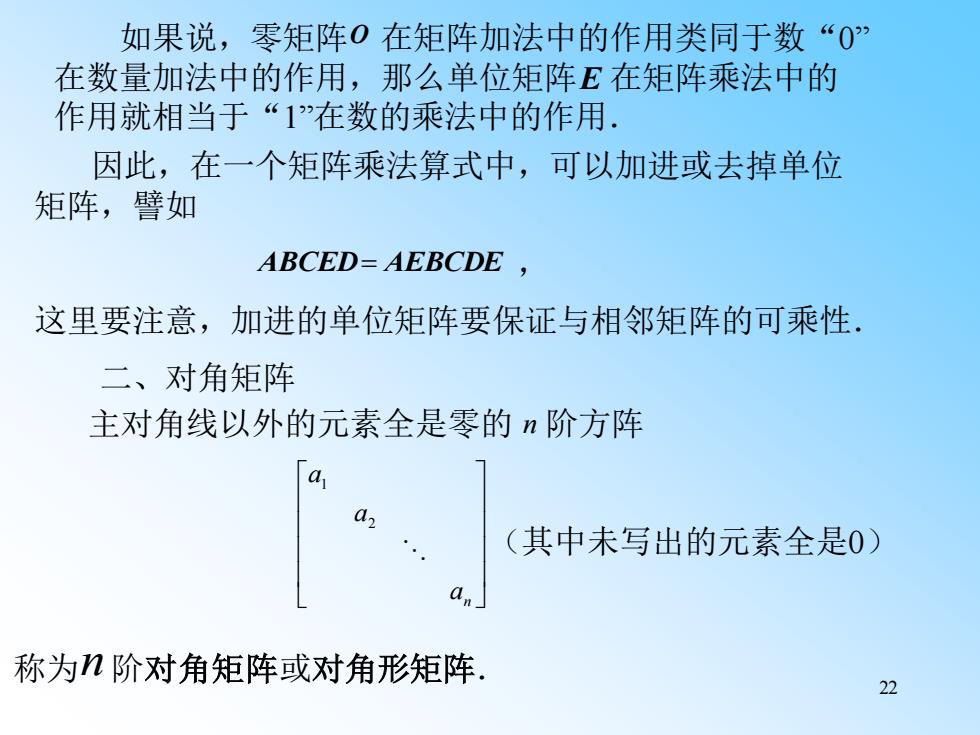
如果说,零矩阵0在矩阵加法中的作用类同于数“0” 在数量加法中的作用,那么单位矩阵E在矩阵乘法中的 作用就相当于“1”在数的乘法中的作用, 因此,在一个矩阵乘法算式中,可以加进或去掉单位 矩阵,譬如 ABCED=AEBCDE, 这里要注意,加进的单位矩阵要保证与相邻矩阵的可乘性, 二、对角矩阵 主对角线以外的元素全是零的n阶方阵 (其中未写出的元素全是0) 称为n阶对角矩阵或对角形矩阵, 22
22 如果说,零矩阵 在矩阵加法中的作用类同于数“0” 在数量加法中的作用,那么单位矩阵 在矩阵乘法中的 作用就相当于“1”在数的乘法中的作用. O E 因此,在一个矩阵乘法算式中,可以加进或去掉单位 矩阵,譬如 ABCED= AEBCDE , 这里要注意,加进的单位矩阵要保证与相邻矩阵的可乘性. 二、对角矩阵 称为 阶对角矩阵或对角形矩阵. 主对角线以外的元素全是零的 阶方阵 (其中未写出的元素全是0) n n an a a 2 1
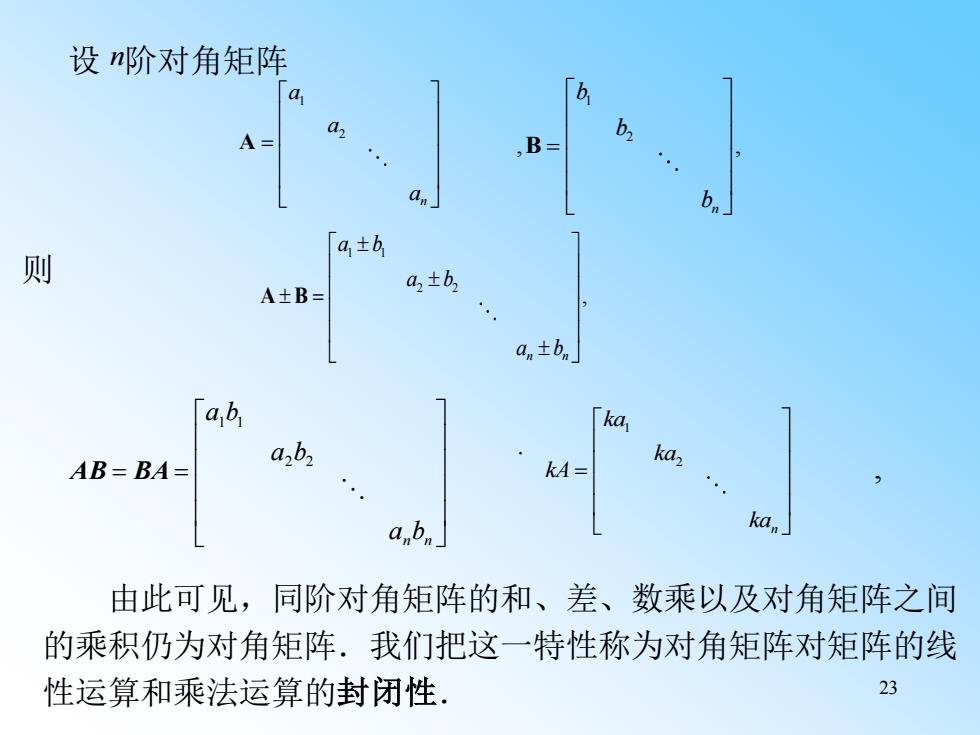
设n阶对角矩阵 ,B= b, A a b. a1±b 则 a2±b, an±bn」 ab 「ka AB=BA- kaz KA kan 由此可见,同阶对角矩阵的和、差、数乘以及对角矩阵之间 的乘积仍为对角矩阵.我们把这一特性称为对角矩阵对矩阵的线 性运算和乘法运算的封闭性 23
23 1 2 n ka ka kA ka = , = = an bn a b a b 2 2 1 1 AB BA . 由此可见,同阶对角矩阵的和、差、数乘以及对角矩阵之间 的乘积仍为对角矩阵.我们把这一特性称为对角矩阵对矩阵的线 性运算和乘法运算的封闭性. 设 n 阶对角矩阵 1 2 n a a a = A 1 2 , , n b b b = B 1 1 2 2 , n n a b a b a b = A B 则