导航 课堂·重难突破 探究一统计在生活中的应用 【例1】甲、乙两人在相同条件下各打靶10次,每次打靶的成 绩情况如图所示: 环数 10 甲:-- 8 十-甲 乙: 6 4 2 0 12 345678910次数
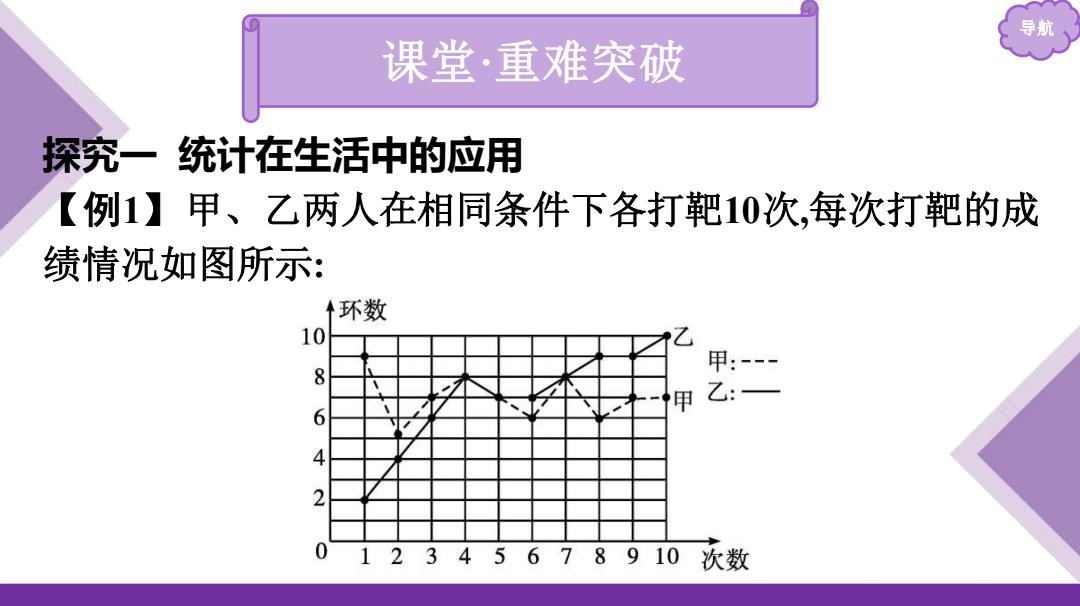
导航 课堂·重难突破 探究一 统计在生活中的应用 【例1】甲、乙两人在相同条件下各打靶10次,每次打靶的成 绩情况如图所示:
1)填写下表: 导航 项目 平均数 方差 中位数 命中9环及以上 甲 1.2 1 5.4 3 (2)请从四个不同的角度对这次测试进行分析: ①从平均数和方差结合分析偏离程度; ②从平均数和中位数结合分析谁的成绩好些; ③从平均数和命中9环及以上的次数相结合看谁的成绩好些; ④从折线图上两人射击命中环数及走势分析谁更有潜力
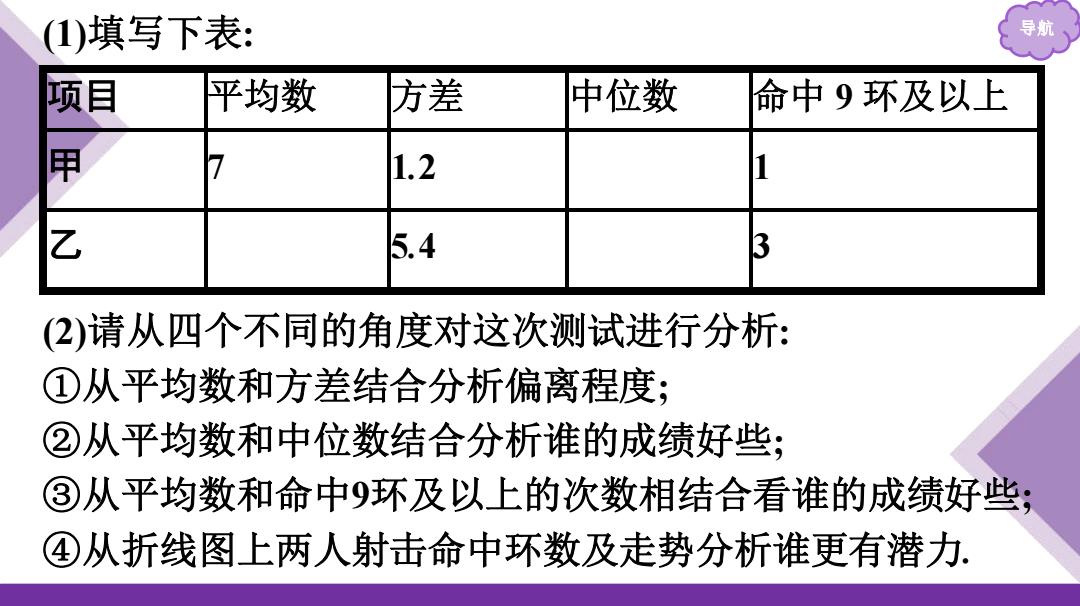
导航 (1)填写下表: 项目 平均数 方差 中位数 命中 9 环及以上 甲 7 1.2 1 乙 5.4 3 (2)请从四个不同的角度对这次测试进行分析: ①从平均数和方差结合分析偏离程度; ②从平均数和中位数结合分析谁的成绩好些; ③从平均数和命中9环及以上的次数相结合看谁的成绩好些; ④从折线图上两人射击命中环数及走势分析谁更有潜力

分析:先从图中读取甲、乙两人的成绩(环数),再通过计算平航 均数、方差等解答其他问题 解:1)乙的射靶环数依次为2,4,68,7,7,8,9,9,10. 所以x2=x2+4H6+87+7+8+99+10)=73乙的射靶环教从小 到大排列为2,4677,8899,10,所以中位数是7生87.5 2 甲的射靶环数从小到大排列为5,6,6,7,7,7,7,8,8,9,所以中位数 为7.于是填充后的表格如下表所示: 项目 平均数 方差 中位数 命中9环及以上 甲 7 1.2 7 1 乙 7 5.4 7.5 3
分析 导航 :先从图中读取甲、乙两人的成绩(环数),再通过计算平 均数、方差等解答其他问题. 解:(1)乙的射靶环数依次为2,4,6,8,7,7,8,9,9,10. 所以𝒙 乙 = 𝟏 𝟏𝟎 ×(2+4+6+8+7+7+8+9+9+10)=7;乙的射靶环数从小 到大排列为 2,4,6,7,7,8,8,9,9,10,所以中位数是𝟕+𝟖 𝟐 =7.5; 甲的射靶环数从小到大排列为5,6,6,7,7,7,7,8,8,9,所以中位数 为7.于是填充后的表格如下表所示: 项目 平均数 方差 中位数 命中9环及以上 甲 7 1.2 7 1 乙 7 5.4 7.5 3

2)①甲、乙成绩的平均数相同,均为7,但s晕<s2,说明甲偏 离平均数的程度小,而乙偏离平均数的程度大 ②甲、乙成绩的平均数相同,而乙成绩的中位数比甲大,说明 乙射靶成绩比甲好. ③甲、乙成绩的平均数相同,而乙命中9环及以上的次数比甲 多2次,可知乙的射靶成绩比甲好. ④从折线图上看,乙的成绩呈上升趋势,而甲的成绩在平均线 上波动不大,说明乙的状态在提升,更有潜力. 反思感悟平均数反映的是总体取值的平均水平,方差(标准差) 反映的是数据的离散程度
导航 (2)①甲、乙成绩的平均数相同,均为7,但 ,说明甲偏 离平均数的程度小,而乙偏离平均数的程度大. ②甲、乙成绩的平均数相同,而乙成绩的中位数比甲大,说明 乙射靶成绩比甲好. ③甲、乙成绩的平均数相同,而乙命中9环及以上的次数比甲 多2次,可知乙的射靶成绩比甲好. ④从折线图上看,乙的成绩呈上升趋势,而甲的成绩在平均线 上波动不大,说明乙的状态在提升,更有潜力. 反思感悟 平均数反映的是总体取值的平均水平,方差(标准差) 反映的是数据的离散程度. 𝒔 甲 𝟐 < 𝒔 乙 𝟐