
全程设计 第六章 平面向量初步 6.1 平面向量及其线性运算 6.1.3 向量的减法
第六章 平面向量初步 6.1 平面向量及其线性运算 6.1.3 向量的减法

课前·基础认知 课堂·重难突破
课前·基础认知 课堂·重难突破

导航 课前·基础认知 一、向量的减法 【问题思考】 1.若小明从家去学校用a表示,从家到超市用b表示,从学校去 超市用c表示,你知道a,b,c是什么关系吗? 提示:c=b-a.(或a+c=b)
导航 课前·基础认知 一、向量的减法 【问题思考】 1.若小明从家去学校用a表示,从家到超市用b表示,从学校去 超市用c表示,你知道a,b,c是什么关系吗? 提示:c=b-a.(或a+c=b)

导 2.填空:(1)一般地,平面上任意给定两个向量a,b,如果向量x能 够满足b+x=a,则称x为向量a与b的,并记作x= (2)在平面内任取一点O,作0A=a,0B=b,作出向量BA,向量BA就 是向量a与b的差(也称BA为向量a与b的差向量),即OA一 OB=BA这种求两向量差的作图方法也常称为向量减法的三 角形法则. 3.两个向量的差是向量还是实数? 提示:向量
导航 2.填空:(1)一般地,平面上任意给定两个向量a,b,如果向量x能 够满足b+x=a,则称x为向量a与b的差,并记作x= a-b . (2)在平面内任取一点 O,作𝑶 𝑨 =a,𝑶 𝑩 =b,作出向量𝑩 𝑨 ,向量𝑩 𝑨 就 是向量 a 与 b 的差(也称𝑩 𝑨 为向量 a 与 b 的差向量),即𝑶 𝑨 − 𝑶 𝑩 = 𝑩 𝑨 .这种求两向量差的作图方法也常称为向量减法的三 角形法则. 3.两个向量的差是向量还是实数? 提示:向量
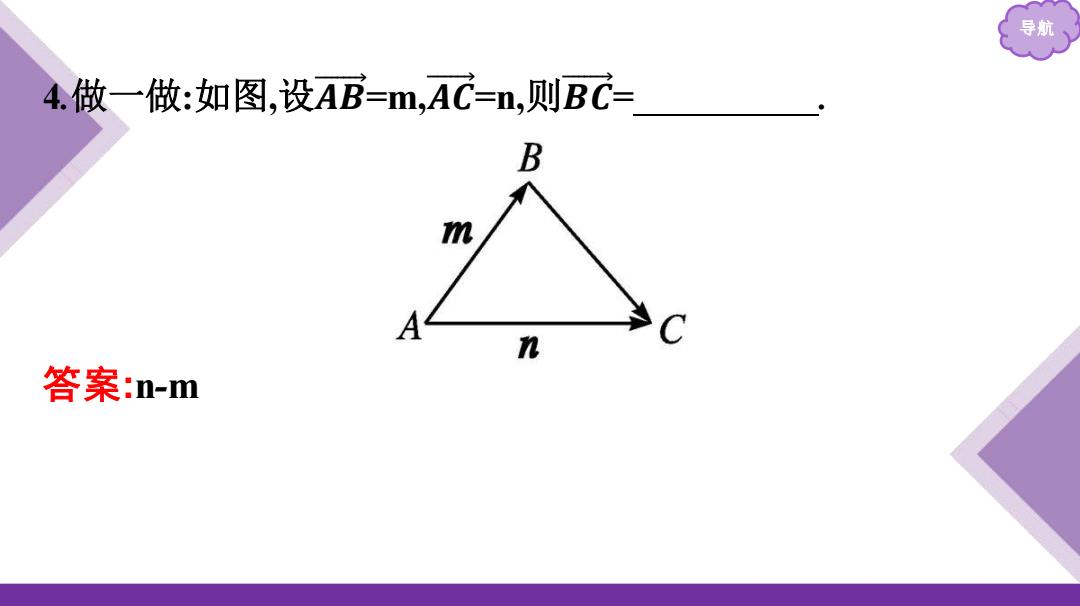
导航 4.做一做:如图,设AB=m,AC=n,则BC= B m A n C 答案:n-m
导航 4.做一做:如图,设𝑨 𝑩 =m,𝑨 𝑪 =n,则𝑩 𝑪 = . 答案:n-m