
全程设计 第六章 平面向量初步 6.3 平面向量线性运算的应用
第六章 平面向量初步 6.3 平面向量线性运算的应用

课前·基础认知 课堂·重难突破
课前·基础认知 课堂·重难突破

导航 课前·基础认知 向量在平面几何中的应用 【问题思考】 1.证明线段平行问题,常用向量平行(共线)的等价条件:若 a=(c1y1),b=(c2y2),则alb(b≠0)台 → 2.求线段的长度或证明线段相等,可利用向量的线性运算、向 量模的公式a=√x2+y2(a=(xy)
导航 课前·基础认知 一、向量在平面几何中的应用 【问题思考】 1.证明线段平行问题,常用向量平行(共线)的等价条件:若 a=(x1 ,y1 ),b=(x2 ,y2 ),则a∥b(b≠0)⇔ a=λb ⇔ x1 y2=x2 y1 . 2.求线段的长度或证明线段相等,可利用向量的线性运算、向 量模的公式|a|= 𝒙 (a=(x,y)). 𝟐 + 𝒚 𝟐

导航 二、向量在物理中的应用 【问题思考】 涉及力、速度、加速度等物理量的运算问题可利用向量的知 识求解
导航 二、向量在物理中的应用 【问题思考】 涉及力、速度、加速度等物理量的运算问题可利用向量的知 识求解
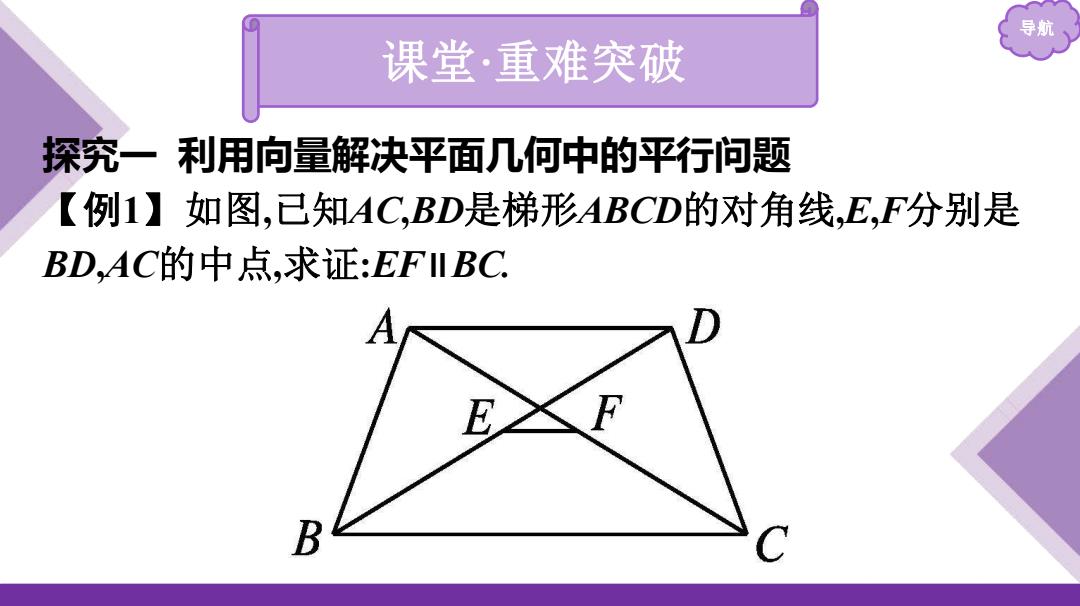
导航 课堂·重难突破 探究一利用向量解决平面几何中的平行问题 【例1】如图,已知AC,BD是梯形ABCD的对角线,E,F分别是 BD,AC的中点,求证:EF Il BC. E B C
导航 课堂·重难突破 探究一 利用向量解决平面几何中的平行问题 【例1】如图,已知AC,BD是梯形ABCD的对角线,E,F分别是 BD,AC的中点,求证:EF∥BC