
dx+8例1判别反常积分的收敛性x4+1解:0<4/33根据比较审敛法1,dx+8收敛.反常积分/x*+1
例1 1 3 4 . 1 dx x + + 判别反常积分 的收敛性 解 , 1 1 1 1 0 3 4 3 4 4 / 3 x x x = + 1, 3 4 p = 根据比较审敛法1, 1 3 4 . 1 dx x + + 反常积分 收敛

定理4(极限审敛法1)设函数f(x)在区间[a,+o0)(a>0)上连续,且f(x)≥0.如果存在常数p>1,使得lim xPf(x)存在,则(f(x)dx收敛;x+8如果 lim xf(x) =d >0 (或 lim xf(x) = +oo),则X-→+80X→+8. f(x)dx发散.dx+8例2判别反常积分的收敛性。x/1+x?1 lim x?.解=1,所给反常积分收敛,xV1+x=X-→>+00
发散. 如 果 或 则 使 得 存在,则 收敛; 上连续,且 如果存在常数 , 定 理 极限审敛法1 设函数 在区间 + →+ →+ + →+ = = + + a x x a p x f x dx xf x d xf x x f x f x dx a f x p f x a ( ) lim ( ) 0 ( lim ( ) ), lim ( ) ( ) ( 0) ( ) 0. 1 4( ) ( ) [ , ) 例2 1 2 . 1 dx x x + + 判 别 反 常 积 分 的 收敛性 解 1, 11 lim 2 2 = + →+ x x x x 所给反常积分收敛.
t3/2+8例3判别反常积分dx的收敛性11+xt3/2xVx解·:limxlim=+8,1+x?x→+01 + x?x-→+根据极限审敛法1,所给反常积分发散+ arctan x&的收敛性例 4 判别反常积分J1xarctanx元解lim xlim arctanx :2x-→+0xx-→+根据极限审敛法1,所给反常积分发散
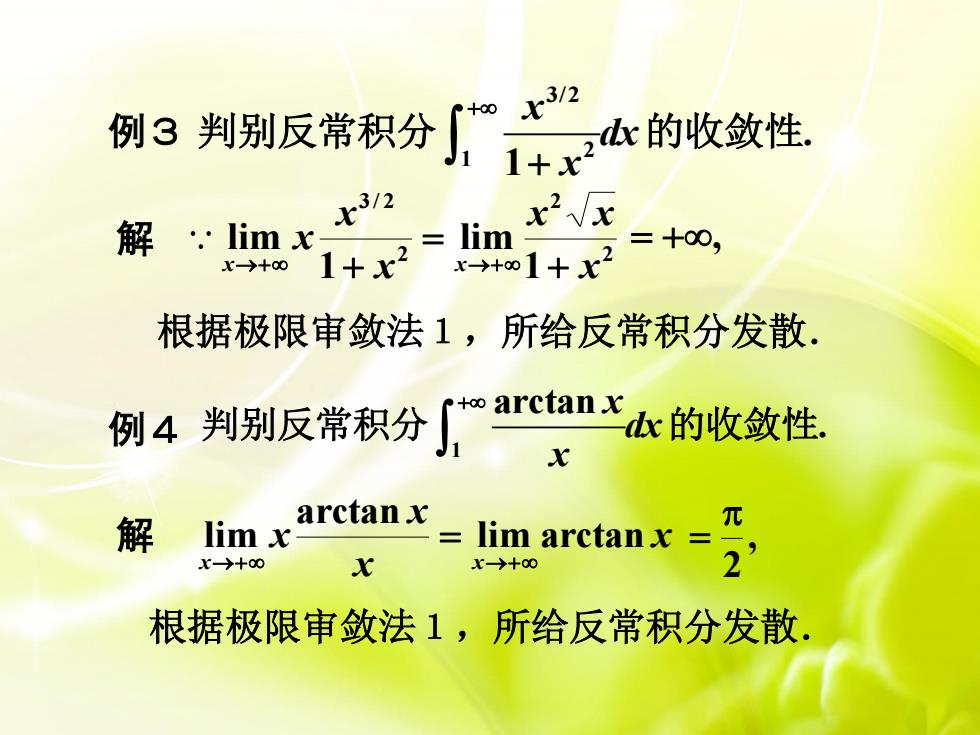
例3 3/2 2 1 . 1 x dx x + + 判别反常积分 的收敛性 解 2 2 2 3 / 2 1 lim 1 lim x x x x x x x x + = →+ + →+ = +, 根据极限审敛法1,所给反常积分发散. 例4 1 arctan . x dx x + 判别反常积分 的收敛性 解 x x x x x x lim arctan arctan lim →+ →+ = , 2 = 根据极限审敛法1,所给反常积分发散.