
例1 证明:当x→0时,tanx-sinx为x的三阶无穷小tan x -sin x解··limt3x-→0sin x1-cosxlinx-→0xcosx1sinx11cosxlim= limlim2’x→0x-→0x-0 cos xx.tanx一sinx为x的三阶无穷小店高等数学(上册)
例1 证明 :当x 0时,tan x sin x为x的三阶无穷小. 解 3 0 tan sin lim x x x x ) sin 1 cos cos 1 lim( 2 0 x x x x x x , 2 1 tan x sin x为x的三阶无穷小. 2 0 0 0 1 cos lim sin lim cos 1 lim x x x x x x x x
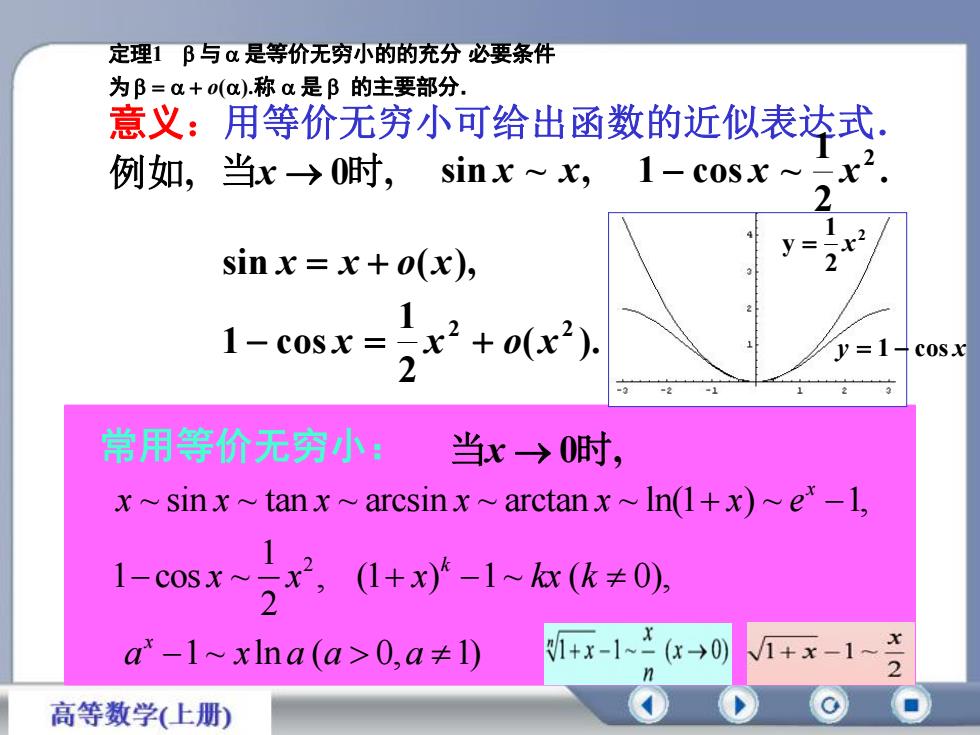
定理1β与α是等价无穷小的的充分必要条件为β=α+o(α).称α是β的主要部分,意义:用等价无穷小可给出函数的近似表达式例如,当x→0时,sinx ~ x,1-cosx ~21七2sin x = x + o(x)1-cosx=y=1cos.x2常用等价无穷小:当x→0时,x~sinx~tanx~arcsinx~arctanx~ln(1+x)~e*-11(1+x)k-1~kx(k0)1-cosx~2x/1+x-1~=(x→0)1+x-1~a-l~xlna(a>0,a±l)2中高等数学(上册)
意义:用等价无穷小可给出函数的近似表达式. 例如, sin x x o(x), ( ). 2 1 1 cos 2 2 x x o x 当x 0时, y 1 cos x 2 2 1 y x 常用等价无穷小: 当x 0时, 2 ~ sin ~ tan ~ arcsin ~ arctan ~ ln(1 ) ~ 1, 1 1 cos ~ , (1 ) 1~ ( 0), 2 1~ ln ( 0, 1) x k x x x x x x x e x x x kx k a x a a a . 2 1 sin ~ , 1 cos ~ 2 x x x x 为 称 是 的主要部分. 定理 与 是等价无穷小的的充分 必要条件 ( ). 1 o

常用等价无穷小:当x→0时,x~ sin x ~ tan x ~arcsin x ~ arctan x~ ln(1+ x)~e -1,12(1+x)*-1~ kx(k0)1-cosx~2x/1+x-1~=(x→0)V1+x-1~2a-l~xlna(a>0,al)n再次验证上节课的内容:tan xarcsin xI-cosx求 lim求lim求lim2x-0x-0xxx-→0-1e'ln(1 + x)求 lim求 limx0x-0xx高等数学(上册)
再次验证上节课的内容: 0 ln(1 ) lim ; x x x 求 0 1 lim . x x e x 求 常用等价无穷小: 当x 0时, 2 ~ sin ~ tan ~ arcsin ~ arctan ~ ln(1 ) ~ 1, 1 1 cos ~ , (1 ) 1~ ( 0), 2 1~ ln ( 0, 1) x k x x x x x x x e x x x kx k a x a a a 0 tan lim ; x x x 求 0 arcsin lim ; x x x 求 2 0 1 cos lim ; x x x 求