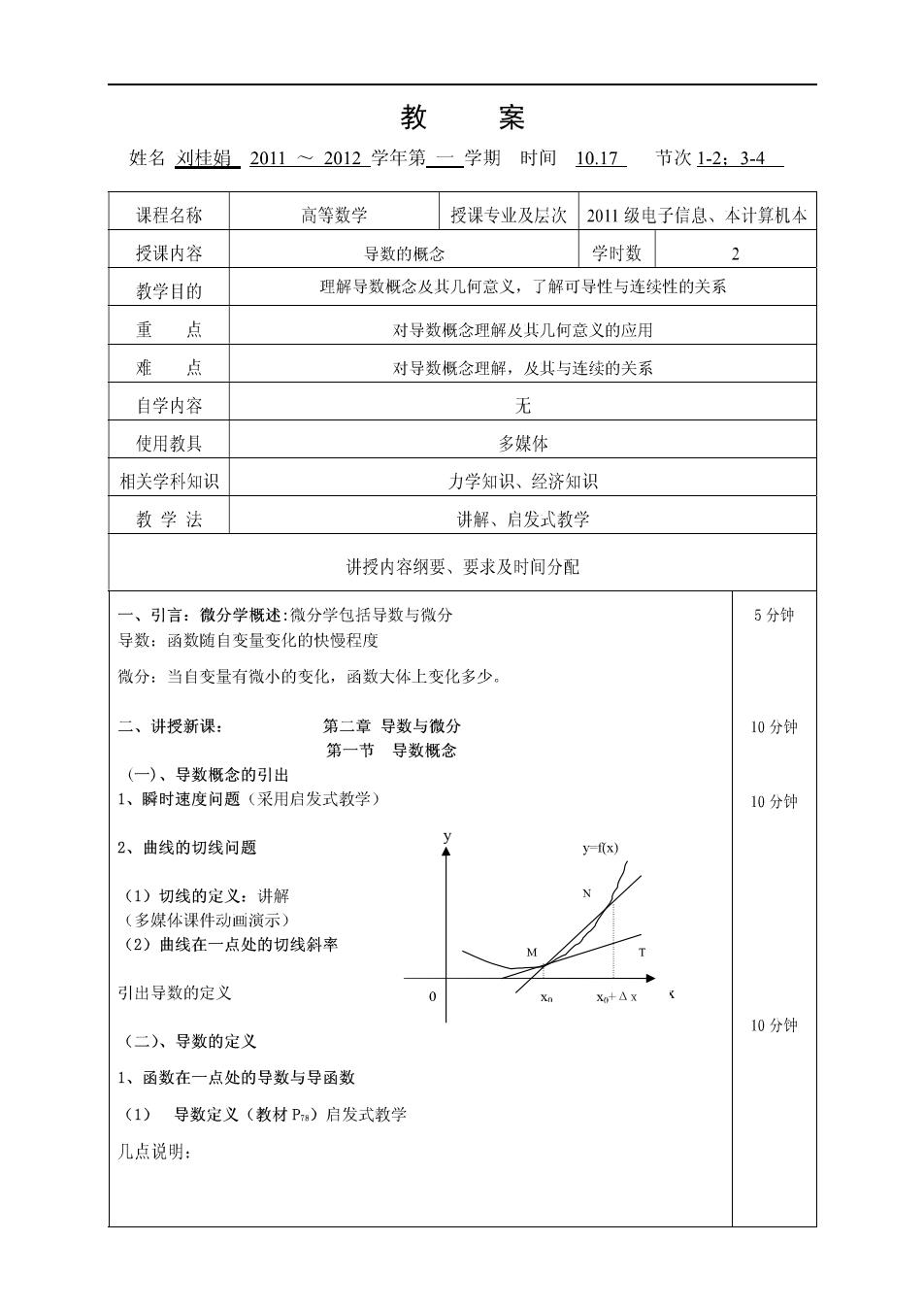
教 案 姓名刘桂娟2011~2012学年第一学期时间10.17节次12:3-4 课程名称 高等数学 授课专业及层次2011级电子信息、本计算机本 授课内容 导激的概念 学时数 2 教学目的 理解导数概念及其几何意义,了解可导性与连续性的关系 重点 对导数概念理解及其几何意义的应用 难点 对导数概念理解,及其与连续的关系 自学内容 无 使用教具 多媒体 相关学科知识 力学知识、经济知识 教学法 讲解、启发式教学 讲授内容纲要、要求及时间分配 引言:微分学概述:微分学包括导数与微分 5分钟 导数:函数随自变量变化的快慢程度 微分:当自变量有微小的变化,函数大体上变化多少。 二、讲授新课: 第二章导数与微分 10分钟 第一节导数概念 (一)、导数概念的引出 1、瞬时速度问题(采用启发式教学) 10分钟 2、曲线的切线问题 (1)切线的定义:讲解 (多媒体课件动画演示) (2)曲线在一点处的切线斜率 引出导数的定义 X A 10分钟 (二入、导数的定义 1、函数在一点处的导数与导函数 (1)导数定义(教材P)启发式教学 几点说明:

讲授内容纲要、要求及时间分配(附页) 1)导数定义及几种常见形 2)函数变化率问题 (2)导函数 2、求导数举例(引导启发讲解 15分钟 例1、求函数/()=C的导数 例2、求幂函数y=x的导数 例3、求函数y=si血x的导数 15分钟 例4、求指数函数f()=a(a>0,a≠)的导数 例5、求函数f(x)=log。x(a>0,a≠1)的导数. 例6、求函数f四=州在x0处的导数 5分钟 3、单侧导 左导数 右导数 (三)、导数的几何意义 15分钟 1几何意义 2、曲线在点M处的切线方程、法线方程 3、应用:讲解例7、例8 (四)、函数的可导性与连续性的关系 函数在某点处可导在该点处必连续:函数在某点连续未必在该点处可导。 10分钟 举例:讲解例9、例10 三、学生习作,教师答疑 四、课堂总结:加强对导数概念的理解,会用定义求简单函数的导数,会求曲线在一点 处的切线方程与法线方程 5分钟 布置作业:习题2-11.9.(6)(7)13.17
教 案 姓名刘桂姐2011~2012学年第一学期时间10.19节次1-2:5-6 课程名称 高等数学 授课专业及层次2011级计算机本、电子信息本 授课内容 函数的求导法则 学时数 2 熟练学握基本初等函数的导数公式、四则运算法则。掌握复合函数 教学目的 的求导法,会求反函数的导数 重点 基本初等函数的导数公式,四则运算法则,复合函数求导法则: 难点 复合求导法则的应用:幂指函数的求导。 自学内容 初等函数的求导问题双曲函数与反双曲函数的导数 使用教具 无 相关学科知识 无 教学法 讲解、启发式教学 讲授内容纲要、要求及时间分配 一、复习回顾:1、导数定义 2、导数的几何意义3、几个求导公式 5分钟 二、讲授新课: 第二章导数与微分 第二节求导法则 一)、函数的和、差、积、商的求导法则 15分钟 u(x) 设函数(与()在点x处可导,则a()+B)、“))、(在点x处也 可导,月有 1.[au(x)+Bv(x)]'=au'(x)+Bv'(x); 2.[u(x)x=u(x)v(x)+u(x)v(x); 3号7."m四om时≠0n 2(x) v'(x) 特司=一 (重点讲解公式,只公式3.其余学生课下自己证明) 15分钟 举例示范:讲解例题 例1、y=2x-5x2+3x-7,求y

讲授内容纲要、要求及时间分配(附页) 例2=+4osx-子求r 5分钟 例3、设y=e(sinx+cosx,求y及y0) 例4、y=tanx,求y' 例5y=secx,求y (二)、反函数的求导法则 1、讲解定理2:反函数的导数等于直接函数导数的倒数。(引导分析证明) 10分钟 2、应用:例6、求y=arcsin x的导数 10分钟 例7、求y=arctan的导数 例8、求y=log。x的导数 (nxy= 特别: (三)、复合函数的导数(币点讲解) 1、复合函数求导法则:定理3 10分钟 dydy du 若复合函数在开区间1内可导,则有链式法划 dx du dx 15分钟 (引导分析证明)》 2、应用:按求导法则步骤讲解例9、例10 直接求复合函数的导数讲解例11-例15 (四)基本求导法则与导数公式(归纳总结,要求学生熟记) 初等函数的求导问题(学生课下自学并练习) 例16:双曲函数与反双曲函数的导数 例17:(综合运用) 5分钟 三、学生习作,教师答疑 四、课堂总结:要求熟练掌握基本初等函数的导数公式、四则运算法则, 掌握复合函数的求导法,会求反函数的导数 布置作业:习题2-22(9.10)6(8.9.10)7(3.5.8.)8.(2.4.10)11.(2.9)
教 案 姓名刘桂姐2011~2012学年第一学期时间10.20 节次1-2:3-4 课程名称 高等数学 授课专业及层次2011级计算机本、电子信息本 授课内容 高阶导数 学时数 2 教学目的 了解高阶导数的概仑:会求高阶导数. 重点 会求高阶导数. 难点 用间接方法求n阶导数 自学内容 无 使用教具 无 相关学科知识 物理知识 教学法 讲解、启发式教学 讲授内容纲要、要求及时间分配 复习回顾:1、基本求导公式 2、求导法则 5分钟 二、讲授新课: 第二章导数与微分 第三节高阶导数 (一)、高阶导数的定义 10分钟 1定义: ”号意记作以”密攻 d 2、二阶导数的物理意义 (二)、高阶导数求法举例 1、直接法:山高阶导数的定义遂步求高阶导数。例1.例2(学生自读) 15分钟 讲解: 例3、证明函数y=2-?满足关系式少y”+1=0 例4、求y=e的n阶导数 15分钟 例5、求y=sinx的n阶导数(引导分析求解) 2、间接法:利用已知的高阶导数公式,通过四则运算,变量代换等方法,求出阶导 5分钟