
两种特殊情况: limf(x)=A=廿&>0,3X>0,当x>X时,有 X→十0 f(x)-A<8 limf(x)=A=廿ε>0,3X>0,当x<-X时,有 →-00 f(x)-A<6 几何意义:直线y=A仍是曲线y=fx)的渐近线. 创,u-在8=, +2 都有水平渐近线y=0, 又如,f(x)=1-2x,g(x)=1+2 2 都有水平渐近线y=1. 2009年7月3日星期五 6 目录 上页 下页 返回
2009年7月3日星期五 6 目录 上页 下页 返回 x 1 1 − x 1 o y x x xg x xf − = = 1 1 )(, 1 )( 直线 y = A 仍是曲线 y = f (x ) 的渐近线 . f Ax x = +∞→ )(lim ∀ ε > ,0 ∃ X > ,0 当 x > X 时, 有 )( − Axf < ε f x A x = −∞→ )(lim ∀ ε > ,0 ∃ X > ,0 当 x < − X 时, 有 )( − Axf < ε 几何意义 : 例如, 都有水平渐近线 y = ;0 x x xf −= xg += 21)(,21)( − 都有水平渐近线 y = .1 又如, o x y x + 21 − x − 21 两种特殊情况 :
sinx 例1证明 lim inx=0. X→00 X 取X当x>X时,就有四-0 sinx 因此 lim =0 X-→o0X 注:y=0是y= Sinx 的水平渐近线。 X 2009年7月3日星期五 7 目录 上页 下页 返回
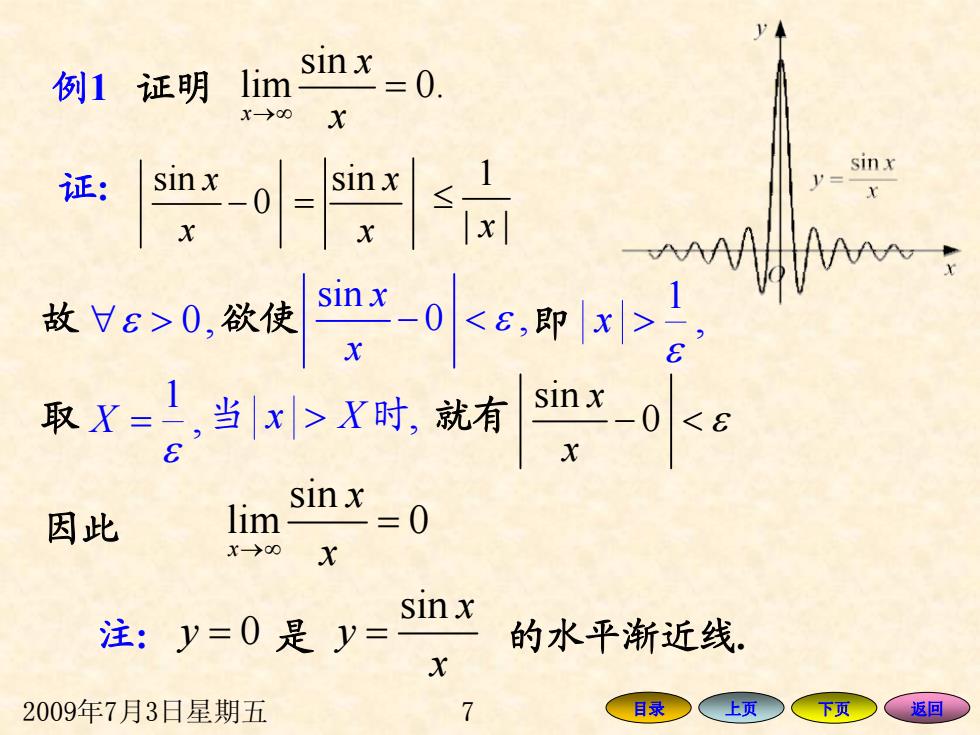
2009年7月3日星期五 7 目录 上页 下页 返回 sin lim 0. x x →∞ x = 证 : sin 0 x x − sin x x = 例1 证明 1 | | x ≤ 取 , 1 ε X = 当 > Xx 时, sin 0 x x − < ε 因此 sin lim 0 x x →∞ x = 就有 故 ∀ ε > ,0 欲使 sin 0 , x x − < ε 即 , 1 ε x > 注 : y = 0 是 sin x y x = 的水平渐近线
2.自变量趋于有限值时函数的极限 (Limits Involving Finites) 观系品款=-)当→1时的安化地 y 通过观察,我们可以看到, 2 虽然函数在点x=1处没有定义, 但当x→1时,f(x)与2无限接近 2 2009年7月3日星期五 P 目录 上页 下页 、返回
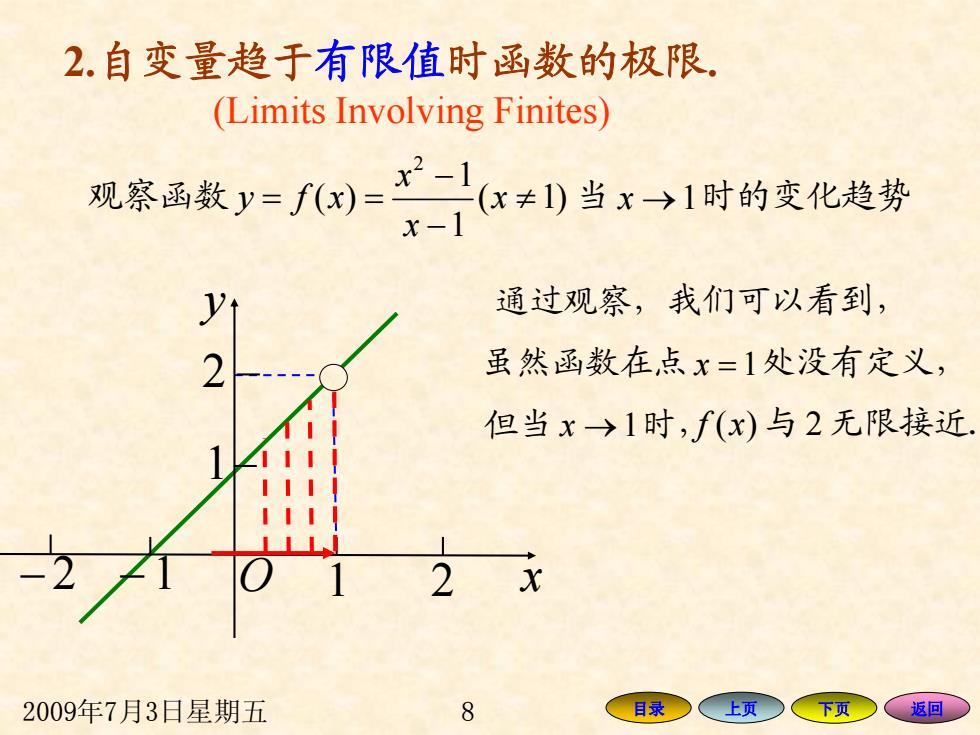
2009年7月3日星期五 8 目录 上页 下页 返回 2.自变量趋于有限值时函数的极限 . (Limits Involving Finites) 观察函数 2 1 ( ) ( 1) 1 x y fx x x − = = ≠ − 当 x → 1时的变化趋势 x y O 1 1 2 − 2 − 1 2 通过观察, 我们可以看到, 虽然函数在点 x = 1处没有定义, 但当 x → 1时, f ( ) x 与 2 无限接近.
(1)双侧极限(Two-sided Limits) 我们用|f(x)-AK表示f(x)与A无限接近. 0<x-<£表示x→x的过程, δ δ Xo x+6 在点x。的去心6邻域中,邻域半径6体现了x与x,的接近程度 2009年7月3日星期五 0 目录 上页 下页 返回
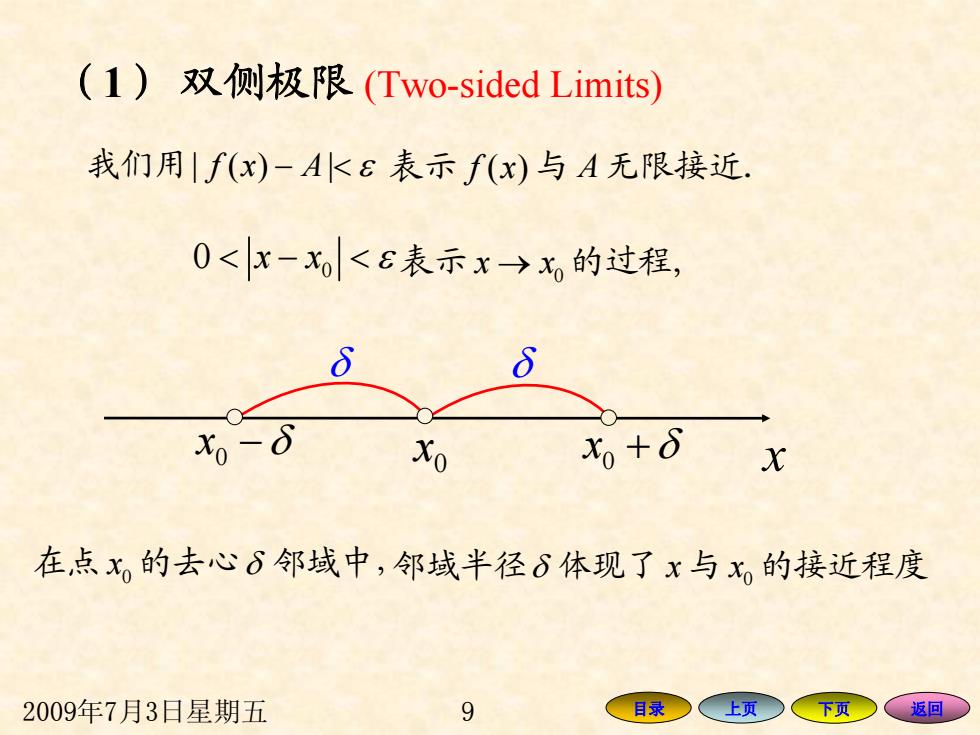
2009年7月3日星期五 9 目录 上页 下页 返回 ( 1) 双侧极限 (Two-sided Limits) 我们用| () | fx A − < ε 表示 f ( ) x 与 A 无限接近. 0 0 <− < x x ε 表示 0 x x → 的过程, 0 x 0 x x − δ 0 x + δ δ δ 在点 0 x 的去心 δ 邻域中,邻域半径 δ 体现了 x 与 0 x 的接近程度