
本节将讨论空间直线及其方程的问题 ■确定空间直线的条件: 空间不平行的两个平面,能且只能确定一条直 线; o 过空间一定点且与已知直线相平行,能且只能 确定一条直线; ■过空间的两个点,能且只能确定一条直线
本节将讨论空间直线及其方程的问题 ◼ 确定空间直线的条件: ◼ 空间不平行的两个平面,能且只能确定一条直 线; ◼ 过空间一定点且与已知直线相平行,能且只能 确定一条直线; ◼ 过空间的两个点,能且只能确定一条直线

§6.4空间直线及其方程 一、 空间直线的一般方程 空间不平行的两个平面必然相交于一条直线,因 此,空间直线可看成两平面的交线。 Π1:A1x+By+C1z+D1=0 Π2:A2x+B2Jy+C23+D2=0 Ax+By+C+D=0 () Ax+B2y+C2+D2=0 空间直线的一般方程
§6.4 空间直线及其方程 x y z o 1 2 空间不平行的两个平面必然相交于一条直线,因 此,空间直线可看成两平面的交线。 1 : A1 x + B1 y + C1 z + D1 = 0 : 0 2 A2 x + B2 y + C2 z + D2 = ( ) 1 1 1 1 2 2 2 2 0 1 0 + + + = + + + = A x B y C z D A x B y C z D 空间直线的一般方程 L 一、空间直线的一般方程
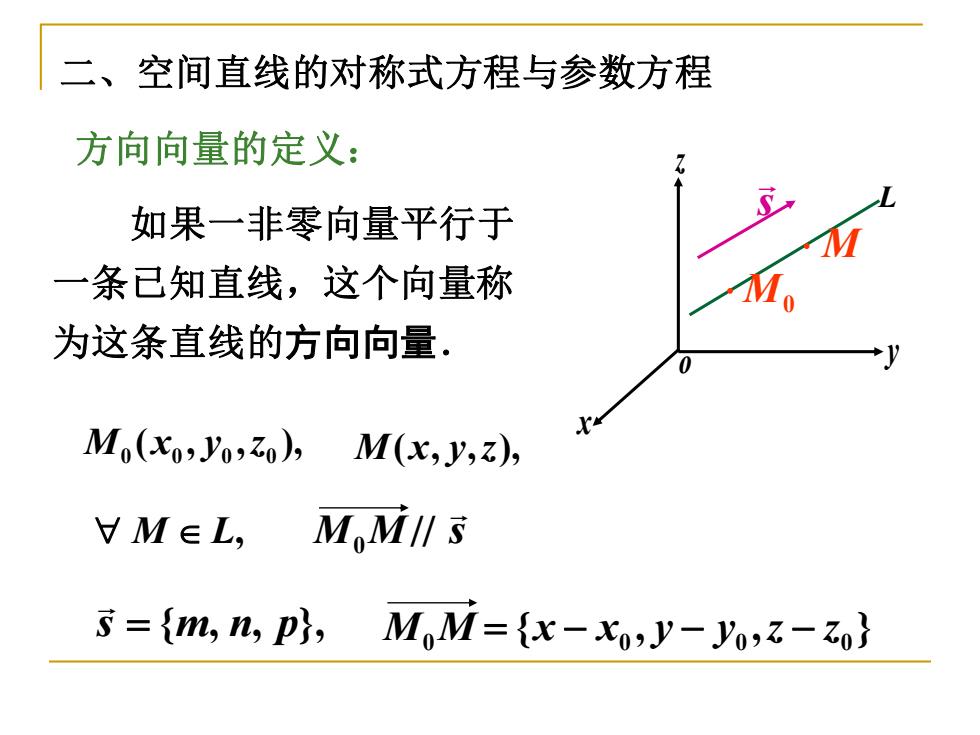
二、空间直线的对称式方程与参数方程 方向向量的定义: 如果一非零向量平行于 一条已知直线,这个向量称 为这条直线的方向向量. Mo(xo2 Fozo), M(x,v,), VM∈L,M,M∥s s={m,n,p),MoM={x-xo,y-yo,-zo}
x y z o 方向向量的定义: 如果一非零向量平行于 一条已知直线,这个向量称 为这条直线的方向向量. s L ( , , ), 0 0 0 0 M x y z M0 M M L, M(x, y,z), M M s 0 // s = {m, n, p}, { , , } 0 0 0 0 M M = x − x y − y z − z 二、空间直线的对称式方程与参数方程
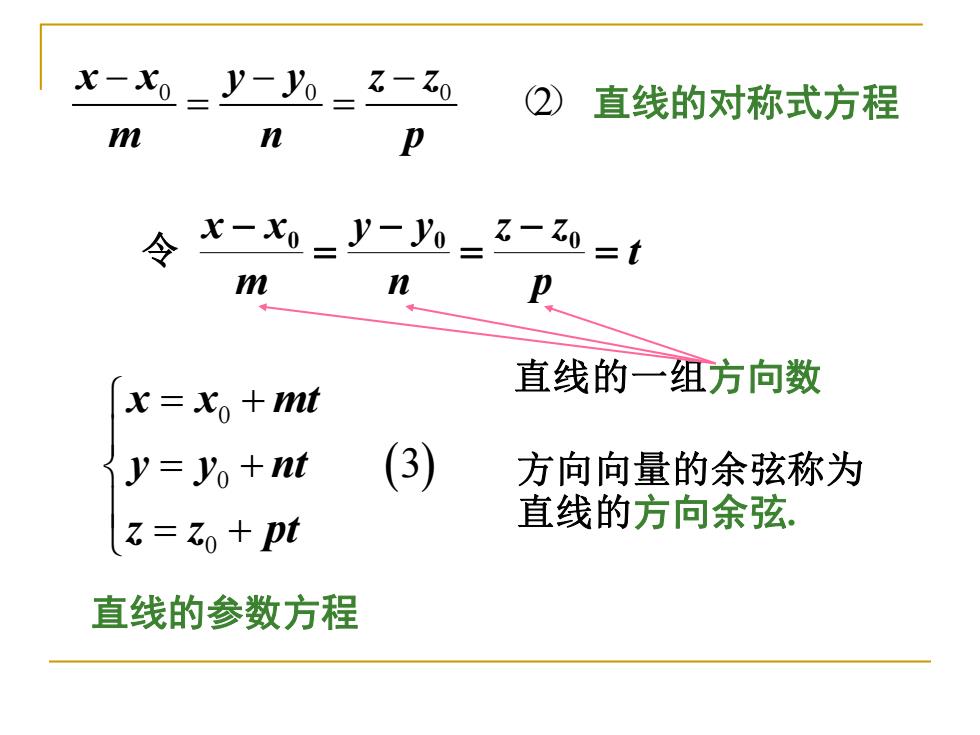
水-=y-0=-0 直线的对称式方程 m n 卫 令x-x0=y-h=-0=t m 直线的一组方向数 x=xo+mt y=yo+nt (3) 方向向量的余弦称为 =Zo+pt 直线的方向余弦 直线的参数方程
0 0 0 2 x x y y z z m n p − − − = = () 直线的对称式方程 t p z z n y y m x x = − = − = 令 − 0 0 0 ( ) 0 0 0 3 x x mt y y nt z z pt = + = + = + 直线的一组方向数 方向向量的余弦称为 直线的方向余弦. 直线的参数方程

例1把直线L的一般方程 2x+y+z-5=0 2x+y-3z-1=0 化为对称式方程和参数式方程。 例2求经过M,(x,乃,),M2(X2,2,2)两点的 直线方程。 例3一直线过点A(2,-3,4),且和y轴垂直 相交,求其方程
例1 把直线 L 的一般方程 2 5 0 2 3 1 0 x y z x y z + + − = + − − = 化为对称式方程和参数式方程。 例2 求经过 1 1 1 1 2 2 2 2 M x y z M x y z ( , , ), ( , , ) 两点的 直线方程。 例3 一直线过点 ,且和 y 轴垂直 相交,求其方程。 A(2, 3, 4) −