
数学模型 第七章 差分方程模型 7.1市场经济中的蛛网模型 7.2减肥计划—节食与运动 7.3差分形式的阻滞增长模型 7.4按年龄分组的种群增长
7.1 市场经济中的蛛网模型 7.2 减肥计划——节食与运动 7.3 差分形式的阻滞增长模型 7.4 按年龄分组的种群增长 第七章 差分方程模型
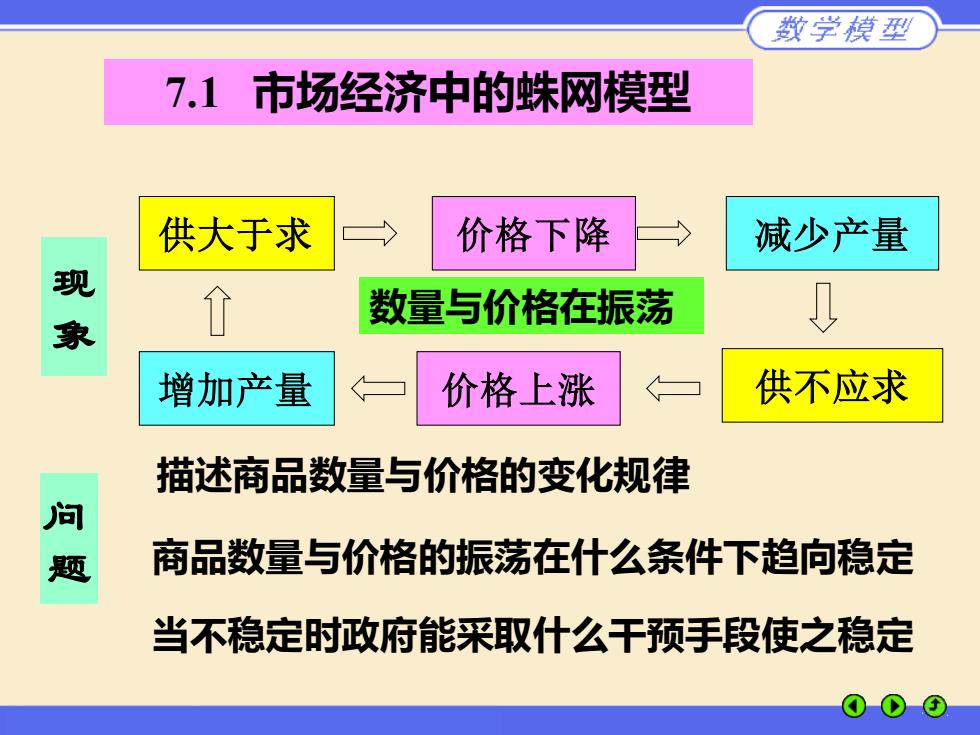
致学模型 7.1市场经济中的蛛网模型 供大于求 价格下降 减少产量 现 数量与价格在振荡 象 增加产量 价格上涨 供不应求 描述商品数量与价格的变化规律 问 题 商品数量与价格的振荡在什么条件下趋向稳定 当不稳定时政府能采取什么干预手段使之稳定
7.1 市场经济中的蛛网模型 问 题 供大于求 现 象 商品数量与价格的振荡在什么条件下趋向稳定 当不稳定时政府能采取什么干预手段使之稳定 价格下降 减少产量 增加产量 价格上涨 供不应求 描述商品数量与价格的变化规律 数量与价格在振荡
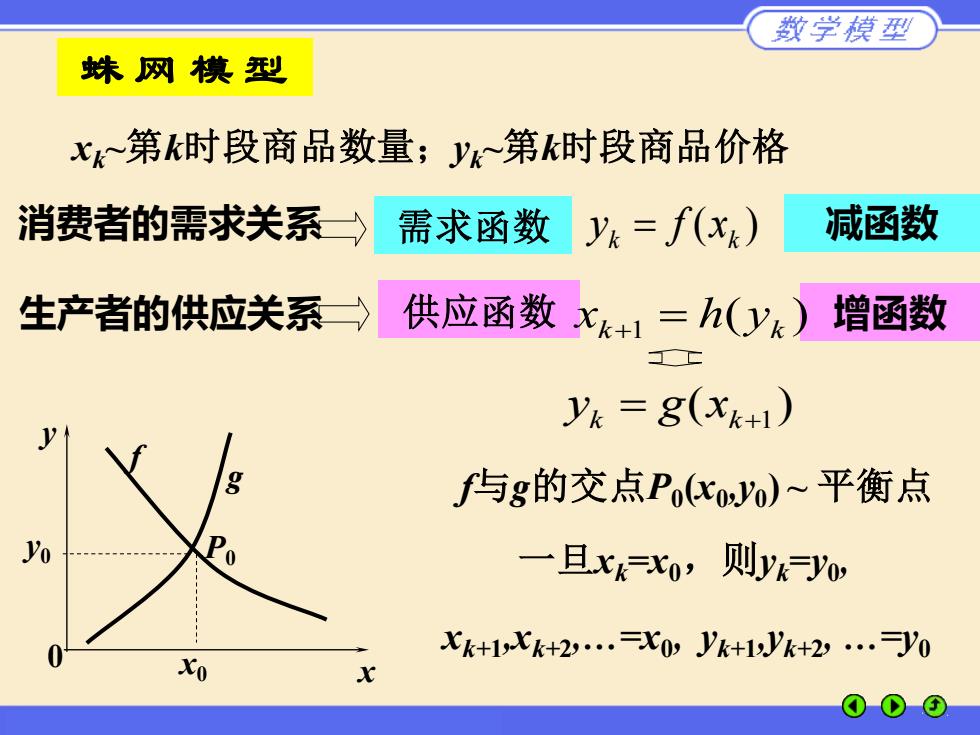
数学模型 蛛网模型 x~第k时段商品数量;y~第k时段商品价格 消费者的需求关系> 需求函数 y=f(x) 减函数 生产者的供应关系) 供应函数 x+=h() 增函数 yk=8(Xk+1) g 与g的交点Pco)~平衡点 Yo 一且x=,则yyo Xk+1Xk+2.X0 k+12Vk+2.0 Xo x
蛛 网 模 型 g x0 y0 P0 f x y 0 xk~第k时段商品数量;yk~第k时段商品价格 消费者的需求关系 ( ) k k y = f x 生产者的供应关系 减函数 供应函数 增函数 需求函数 f与g的交点P0 (x0 ,y0 ) ~ 平衡点 一旦xk=x0,则yk=y0 , xk+1 ,xk+2 ,.=x0 , yk+1 ,yk+2 , .=y0 ( ) k 1 k x = h y + ( ) k = k+1 y g x
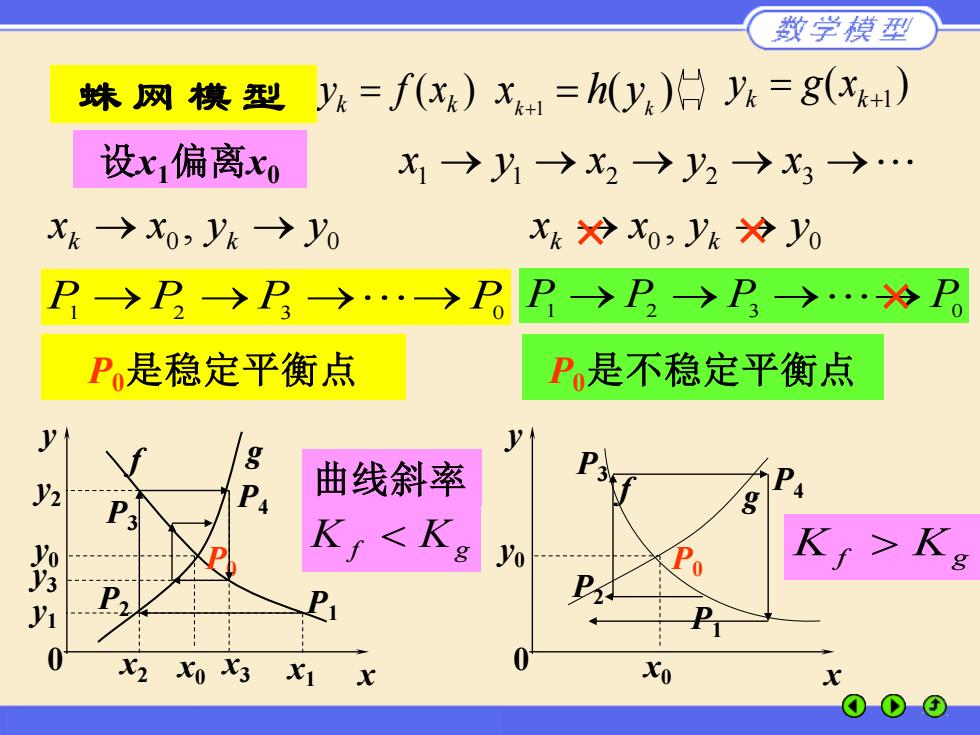
数学模型 蛛网模型 yx=f(xg)x=h(y)y=g(x) 设x偏离x0 X1→y1→X2→y2→X3→. xk→X0,yk)y0 xk冷Xo,yk冷y0 P→P→P>→PP→P→P→.冷P P是稳定平衡点 P是不稳定平衡点 g D V2 曲线斜率 P KI>K P. P 2X03 X1 x 0
x y 0 f g y0 x0 P0 设x1偏离x0 x1 x2 y P2 1 P1 y2 P3 P4 x3 y3 x1 → y1 → x2 → y2 → x3 → P1 → P2 → P3 →→ P0 0 0 x x , y y k → k → P0是稳定平衡点 P1 P2 P3 P4 P0是不稳定平衡点 K f Kg x y 0 y0 x0 P0 f g ( ) k k y = f x ( ) k 1 k x = h y + ( ) k = k+1 y g x 0 0 x x , y y k → k → K f Kg 曲线斜率 蛛 网 模 型 P1 → P2 → P3 →→ P0

数学模型 方程模型 在P点附近用直线近似曲线 %=f(x) yk-y=-a(xk-x)(@>0) xk+=h(yk)1-x0=B(yk-yo)(B>0) X1-x三-Cfx-x) x+1-x。=(-β)(x,-x)》 aB<1(a<1/B)=x4→x P稳定 Kf<Kg aB>1 (a>1/B)x →00 P不稳定 Ki>Kg 方程模型与蛛网模型的一致 a=K 1/B=K
( ) k k y = f x ( ) k 1 k x = h y + 在P0点附近用直线近似曲线 ( ) ( 0) yk − y0 = − xk − x0 ( ) ( 0) xk+1 − x0 = yk − y0 ( ) 1 0 0 x x x x k + − = − k − ( ) ( ) 1 0 1 0 x x x x k k + − = − − 1 P0稳定 P0不稳定 0 x x k → xk → = K f = Kg 1/ ( 1/ ) ( 1/ ) 1 方 程 模 型 K f Kg K f Kg 方程模型与蛛网模型的一致