Malthus模型与Logistic模型 为了保持自然资料的合理开发与利用,人类必须保持并控 制生态平衡,甚至必须控制人类自身的增长。 以下将建立几个简单的单种群增长模型,以简略分析一下 这方面的问题。一般:本乏体的分析可以通过一些简单模型的 复合离散化为连续,方 据生态系统的特征自行建立 相区 便研究 美丽的大自然 种群的数量本应取离散值,但由于种群数 量一般较大,为建立微分方程模型,可将种群 数量看作连续变量,甚至允许它为可微变量, 由此引起的误差将是十分微小的
为了保持自然资料的合理开发与利用,人类必须保持并控 制生态平衡,甚至必须控制人类自身的增长。 以下将建立几个简单的单种群增长模型,以简略分析一下 这方面的问题。一般生态系统的分析可以通过一些简单模型的 复合来研究,大家若有兴趣可以根据生态系统的特征自行建立 相应的模型。 美丽的大自然 种群的数量本应取离散值,但由于种群数 量一般较大,为建立微分方程模型,可将种群 数量看作连续变量,甚至允许它为可微变量, 由此引起的误差将是十分微小的。 离散化为连续,方 便研究 Malthus模型与Logistic模型

模型1马尔萨斯(Malthus)模型 马尔萨斯在分析人口出生与死亡情况的资料后发现,人口 净增长率r基本上是一常数,(r=bd为出生率,为死 亡率),即:1dN N dt =r或 (3.5) (3.1)的解为:N(0=Neu- (3.6) 其中N。=N(t)为初始时刻t时的种群数。 马尔萨斯模型的一个显著特点:种群数量翻一番所需 的时间是固定的。 令种群数量翻一番所需的时间为T,则有:2N。=N,e 故
模型1 马尔萨斯(Malthus)模型 马尔萨斯在分析人口出生与死亡情况的资料后发现,人口 净增长率r 基本上是一常数,(r =b-d,b为出生率,d为死 亡率),即: 1 dN r N dt = dN rN dt 或 = (3.5) 0 ( ) 0 ( ) r t t N t N e − = (3.6) (3.1)的解为: 其中N0 =N(t 0 )为初始时刻t 0时的种群数。 马尔萨斯模型的一个显著特点:种群数量翻一番所需 的时间是固定的。 令种群数量翻一番所需的时间为T,则有: 0 0 2 rT N N e = ln 2 T r 故 =
模型楂 簌历向的姨的像特红料6年[火?的期倪 戌丹何破数铺型邮蘑报结国童土细安 即辣海弹金 的每6年明 Malthus模型实际上口右在胜体兑 扇上抄 所以Malthus模型假设的人口 每34. 净增长率不可能始终保持常数, 它应当与人口数量有关。 级颈的增长 0.5 1950 2000 2050 2100 2150 2200 年
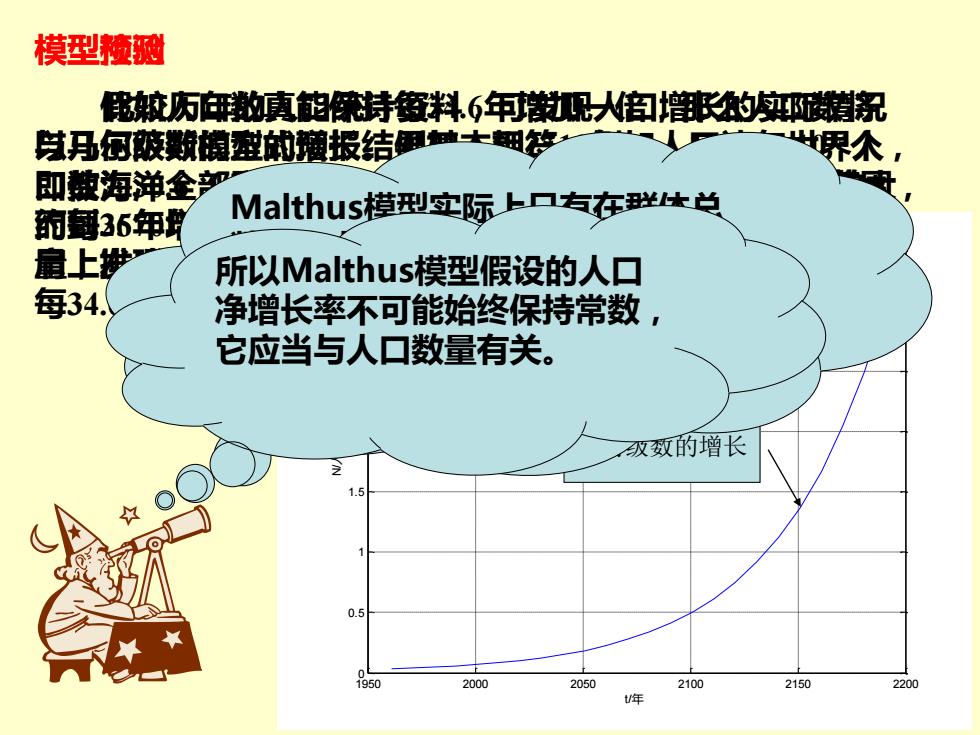
模型检验 比较历年的人口统计资料,可发现人口增长的实际情况 与马尔萨斯模型的预报结果基本相符,例如,1961年世界人 口数为30.6 (即3.06×109),人口增长率约为2%,人口数大 约每35年增加一倍。检查1700年至1961的260年人口实际数 量,发现两者几乎完全一致,且按马氏模型计算,人口数量 每34.6年增加一倍,两者也几乎相同。 1950 2000 2050 2100 2150 2200 0 0.5 1 1.5 2 2.5 3 3.5 x 1011 t /年 N/人 马尔萨斯模型人口预测 模型预测 假如人口数真能保持每34.6年增加一倍,那么人口数将 以几何级数的方式增长。例如,到2510年,人口达2×1014个, 即使海洋全部变成陆地,每人也只有9.3平方英尺的活动范围, 而到2670年,人口达36×1015个,只好一个人站在另一人的 肩上排成二层了。 故马尔萨斯模型是不完善的。 几何级数的增长 Malthus模型实际上只有在群体总 数不太大时才合理,到总数增大时, 生物群体的各成员之间由于有限的 生存空间,有限的自然资源及食物 等原因,就可能发生生存竞争等现 象。 所以Malthus模型假设的人口 净增长率不可能始终保持常数, 它应当与人口数量有关

模型2 Logistic模型 人口净增长率应当与人口数量有关,即:=) 从而右·dM (3.9)式还有另一解释,由于空间和资源都是有限的,不可能供养无限 增长的种群个体,当种群数量过多时,由于人均资源占有率的下降及环境 恶化、疾病增多等原因,出生率将降低而死亡率却会提高。设环境能供养 的种群数量的上界为K(近似地将K看成常数),N表示当前的种群数量, K-N恰为环境还能供养的种群数量,(3.9)指出,种群增长率与两者的乘 积成正比,正好符合统计规律,得到了实验结果的支持,这就是(3.9)也 被称为统计筹算律的原因。 (3.8)可改写成: dN (3.8)被软为6ist心模型或生物总数增恨的统计筹算律,是由荷兰数学生 物学家弗赫斯特(Verhulst)首先提出的。一次项系数是负的,因为当种群数 量很大时,会对自身增大产生抑制性,故一次项又被称为竞争项
模型2 Logistic模型 人口净增长率应当与人口数量有关,即: r=r(N) 从而有: ( ) dN r N N dt = (3.7) r(N)是未知函数,但根 据实际背景,它无法用 拟合方法来求 。 为了得出一个有实际意义的 模型,我们不妨采用一下工 程师原则。工程师们在建立 实际问题的数学模型时,总 是采用尽可能简单的方法。 r(N)最简单的形式是常数,此 时得到的就是马尔萨斯模型。 对马尔萨斯模型的最简单的改 进就是引进一次项(竞争项) 对马尔萨斯模型引入一次项(竞争项),令 r(N)=r-aN 此时得到微分方程: ( ) dN r aN N dt = − (1 ) dN N r N dt K 或 = − (3.8) (3.8)被称为Logistic模型或生物总数增长的统计筹算律,是由荷兰数学生 物学家弗赫斯特(Verhulst)首先提出的。一次项系数是负的,因为当种群数 量很大时,会对自身增大产生抑制性,故一次项又被称为竞争项。 (3.8)可改写成: ( ) dN k K N N dt = − (3.9) (3.9)式还有另一解释,由于空间和资源都是有限的,不可能供养无限 增长的种群个体,当种群数量过多时,由于人均资源占有率的下降及环境 恶化、疾病增多等原因,出生率将降低而死亡率却会提高。设环境能供养 的种群数量的上界为K(近似地将K看成常数),N表示当前的种群数量, K-N恰为环境还能供养的种群数量,(3.9)指出,种群增长率与两者的乘 积成正比,正好符合统计规律,得到了实验结果的支持,这就是(3.9)也 被称为统计筹算律的原因
对(3.9)分离变量: dN=kKdt 两边积分并整理得: N- K 1+Ce版 令N(O)=N,求得: K-N。 N 故(3.9)的满足初始条件N(O)=N的解为: NoK N(t)= No+(K-No)e- (3.10) 易见: 1.5 N0=1.5 Logistic曲线 N(0)=No,lim N(t)=K K=1 N(t)的图形请看图3.5 0.5 N0=0.1 10 20 0 40 50 图3-5
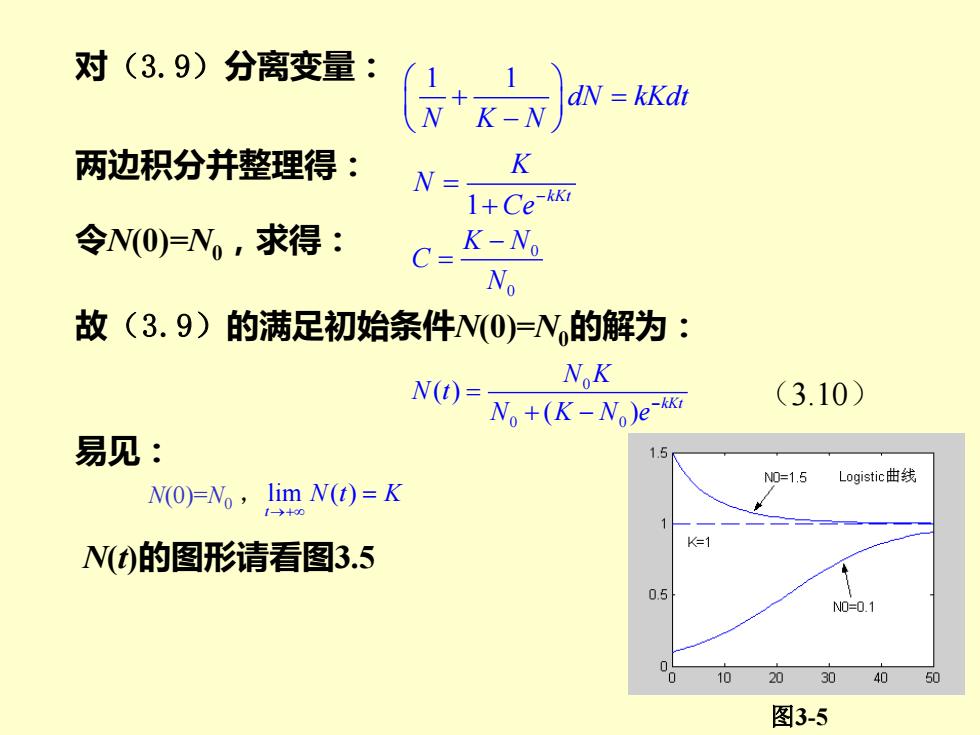
图3-5 对(3.9)分离变量: 1 1 dN kKdt N K N + = − 两边积分并整理得: 1 kKt K N Ce− = + 令N(0)=N0,求得: 0 0 K N C N − = 故(3.9)的满足初始条件N(0)=N0的解为: 0 0 0 ( ) ( ) kKt N K N t N K N e− = + − (3.10) 易见: N(0)=N0 , lim ( ) t N t K →+ = N(t)的图形请看图3.5