《计量经济学》课程教学课件（PPT讲稿）05 多重共线性（Multicollinearity）

中面寒靠大琴红济管视学院 COLLEGE OF ECONOMICS MANAGEMENT.CAL (2)正交的情形：xx2=0,即∑xx2=0 v[图】 2)R(x'x)=2 3)x'x=∑x2∑x号 4)r= ∑x =0 ∑∑好 5)(xx)1=

（2）正交的情形： x1  x2 = 0, 即x1 x2 = 0         =          =       2 2 2 1 2 1 2 2 1 2 2 1 0 0 1) x x x x x x x x x x 2) R(x  x) = 2  =  2 2 2 1 3) x x x x 4) 0 2 2 2 1 1 2 = =    x x x x r              =  −  2 2 2 1 1 1 1 5) ( ) x x x x

中面奥靠大学红济管视学院 COLLEGE OF ECONOMICS MANAGEMENT.CAL (3)多重共线的情形 x2=ax,+y,v满足关于残差项的基本假设。 设 y越小，多重共线性越强：V越大，多重共线性越弱。 ∑xx,=∑x(a+)=a∑x,∑x号=∑(a+2=a2∑x+∑y2 川3 1 2)Rx'x)=2 3)xx=a2(∑x2)2+∑x∑y2-a2(∑x)2=∑∑2

（3）多重共线的情形 越小，多重共线性越强； 越大，多重共线性越弱。 设 满足关于残差项的基本假设。 v , 2 1 v x = ax + v v  = + =   = + =  + 2 2 1 2 2 1 2 2 2 1 2 1 1 1 x x x (ax v) a x , x (ax v) a x v           + =         + =          =             2 1 2 2 2 1 2 2 1 2 2 1 2 1 2 1 2 1 2 2 1 2 2 1 1 1) x v a a a x a x a x v x a x x x x x x x x x  =  +  −  =   = 2 2 1 2 2 1 2 2 2 1 2 2 1 2 3) ( ) ( ) 2) R 2 x x a x x v a x x v (x x )

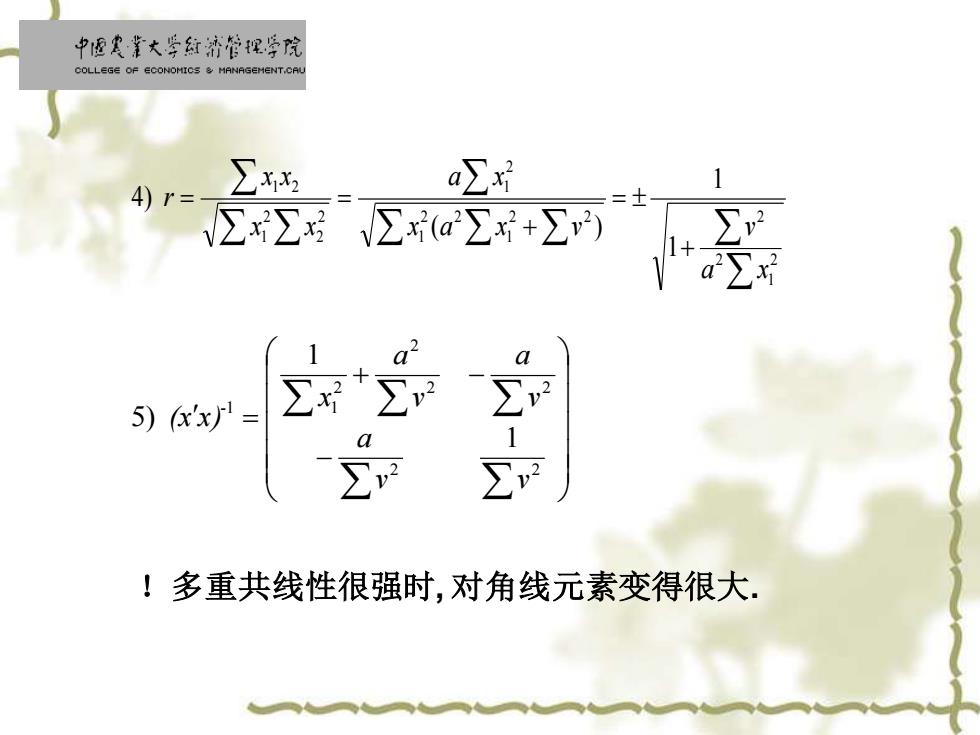
中匣寒靠大学红济管视学院 COLLEGE OF ECONOMICS MANAGEMENT.CAL 4)r= ∑ a 5)x= !多重共线性很强时，对角线元素变得很大

         + =  + = = 2 1 2 2 2 2 1 2 2 1 2 1 2 2 2 1 1 2 1 1 ( ) 4) a x x a x v v a x x x x x r               − + −  =      2 2 2 2 2 2 1 1 1 1 5) v v a v a v a x (x x )- ！多重共线性很强时, 对角线元素变得很大

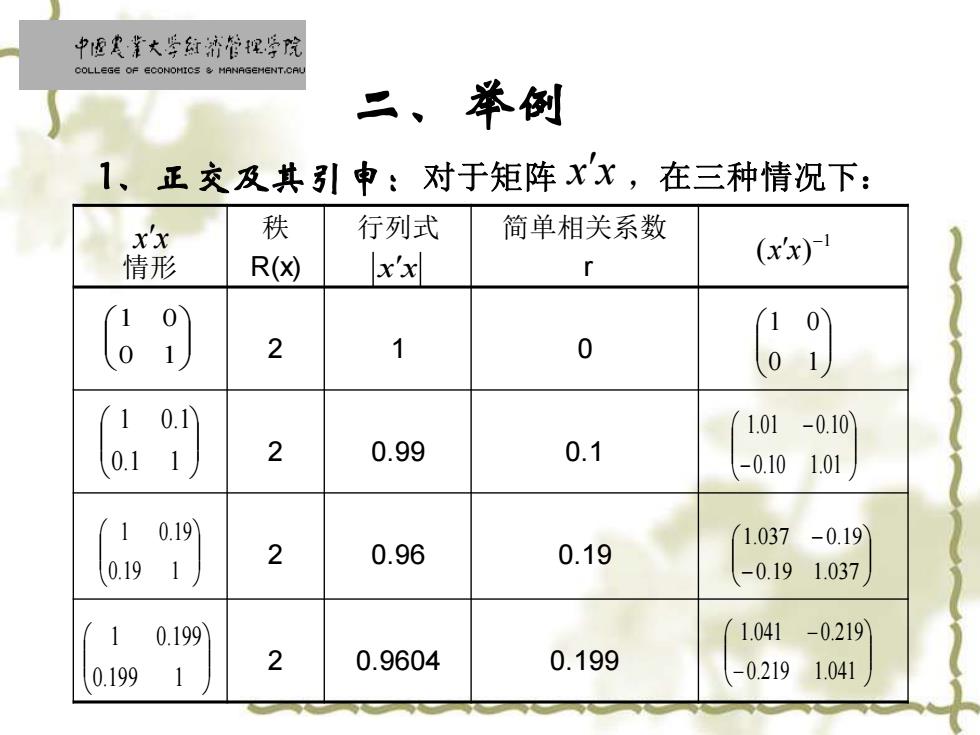
中面史靠大学红济管视学院 COLLEGE OF ECONOMICS MANAGEMENT.CAL 二、举例 1、正交及其引中：对于矩阵xx,在三种情况下： x 秩 行列式 简单相关系数 情形 R() xxl (xx) r 0 1 2 1 0 (1 0.1 1.01-0.10 0.1 1 2 0.99 0.1 -0.101.01 1 0.19 1.037-0.19 0.191 2 0.96 0.19 -0.191.037 1 0.199 1.041 -0.219 2 0.9604 0.199 0.199 -0.219 1.041

二、举例 x  x         0 1 1 0 情形 秩 R(x) 行列式 简单相关系数 r 2 1 0 2 0.99 0.1 2 0.96 0.19 2 0.9604 0.199 1、正交及其引申：对于矩阵 ，在三种情况下： x  x 1 ( ) − x  x         0 1 1 0         0.1 1 1 0.1         0.19 1 1 0.19         0.199 1 1 0.199         − − 0.10 1.01 1.01 0.10         − − 0.19 1.037 1.037 0.19         − − 0.219 1.041 1.041 0.219 x  x

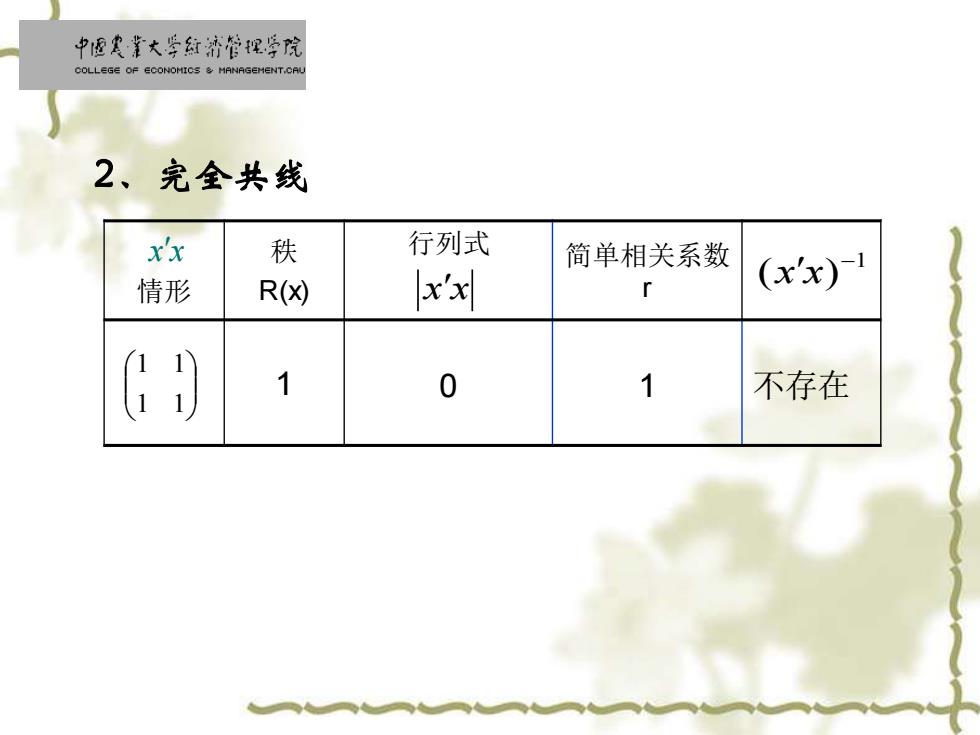
中虚寒靠大季红济管视学院 COLLEGE OF ECONOMICS MANAGEMENT.CAL 2、完全共线 xx 秩 行列式 简单相关系数 情形 R(x) xx r (xx)-1 1 0 1 不存在

2、完全共线         1 1 1 1 情形 秩 R(x) 行列式 简单相关系数 r 1 0 1 不存在 x  x 1 ( ) − x  x x  x