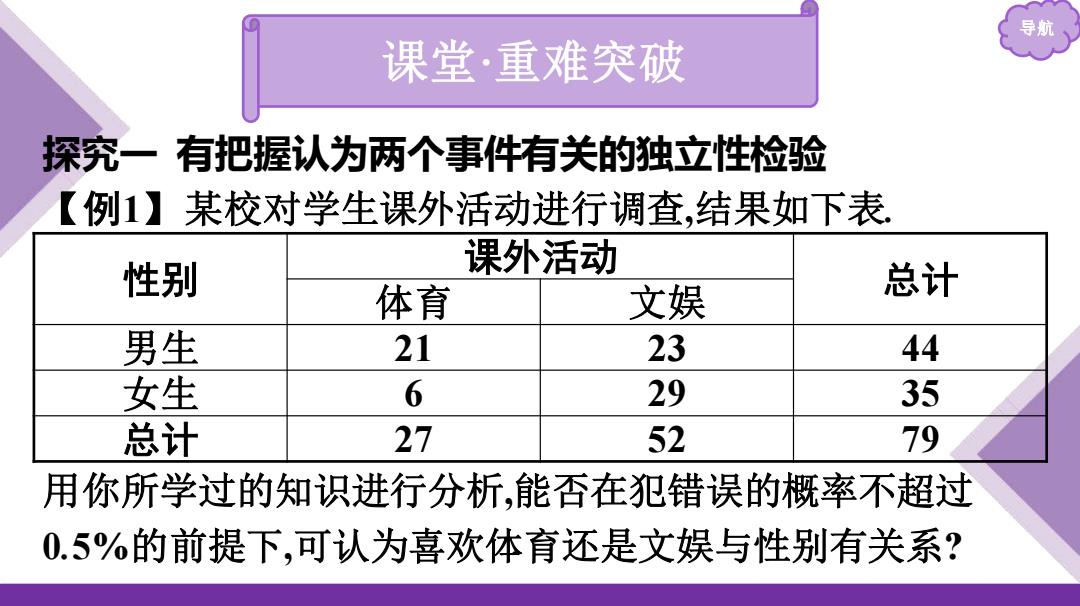
导航 课堂·重难突破 探究一有把握认为两个事件有关的独立性检验 【例1】某校对学生课外活动进行调查,结果如下表 性别 课外活动 体育 文娱 总计 男生 21 23 44 女生 6 29 35 总计 27 52 79 用你所学过的知识进行分析,能否在犯错误的概率不超过 0.5%的前提下,可认为喜欢体育还是文娱与性别有关系?
导航 课堂·重难突破 探究一 有把握认为两个事件有关的独立性检验 【例1】某校对学生课外活动进行调查,结果如下表. 性别 课外活动 总计 体育 文娱 男生 21 23 44 女生 6 29 35 总计 27 52 79 用你所学过的知识进行分析,能否在犯错误的概率不超过 0.5%的前提下,可认为喜欢体育还是文娱与性别有关系?

导航 解:由题意可知,X2_79x21x29-23×6 ≈8.106. 44×35×27×52 又因为查表可得Px2≥7.879)=0.005, 因为8.106>7.879,所以在犯错误的概率不超过0.5%的前提下, 可认为喜欢体育还是文娱与性别有关
导航 解:由题意可知,χ 2 = 𝟕𝟗×(𝟐𝟏×𝟐𝟗-𝟐𝟑×𝟔) 𝟐 𝟒𝟒×𝟑𝟓×𝟐𝟕×𝟓𝟐 ≈8.106. 又因为查表可得P(χ 2≥7.879)=0.005, 因为8.106>7.879,所以在犯错误的概率不超过0.5%的前提下, 可认为喜欢体育还是文娱与性别有关

导航 反思感悟 解决此类问题,先利用x= n(ad-be)2 (a+b)(c+d)(a+c)(b+d) 求出x2的值,再 利用显著性水平α以及对应的分位数k来判断有多大的把握 判断两个事件有关
导航 解决此类问题,先利用 求出χ 2的值,再 利用显著性水平α以及对应的分位数k来判断有多大的把握 判断两个事件有关. χ 2 = 𝒏(𝒂𝒅-𝒃𝒄) 𝟐 (𝒂+𝒃)(𝒄+𝒅)(𝒂+𝒄)(𝒃+𝒅)