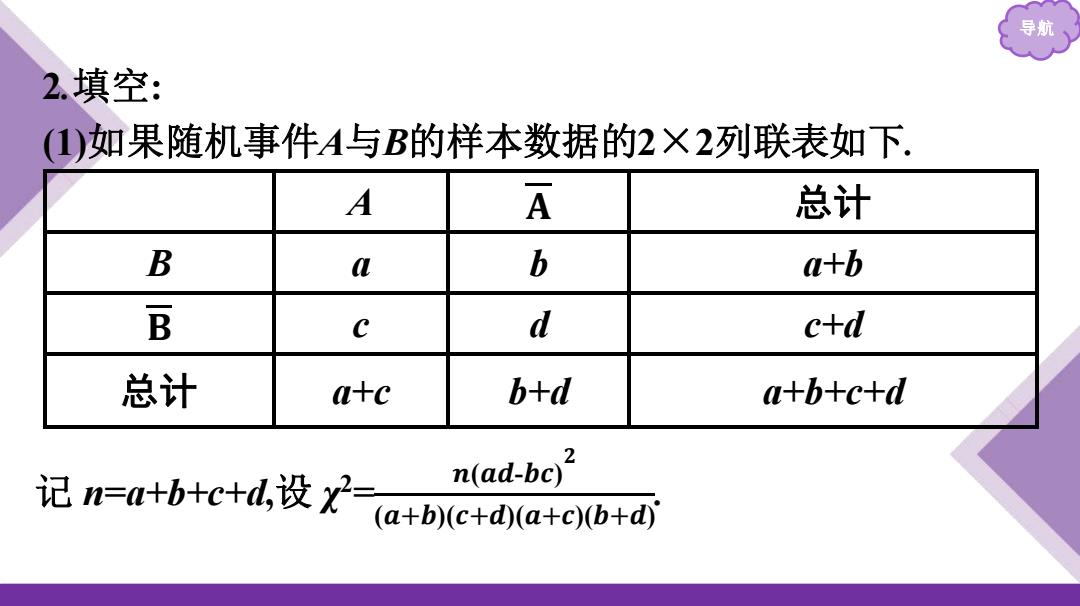
导航 2填空: (1)如果随机事件A与B的样本数据的2×2列联表如下. A A 总计 B L b a+b B c d c+d 总计 a+c b+d a+b+c+d 2 i记n=a+btc+l.设X-e9eo+ n(ad-bc
导航 2.填空: (1)如果随机事件A与B的样本数据的2×2列联表如下. A 𝐀 总计 B a b a+b 𝐁 c d c+d 总计 a+c b+d a+b+c+d 记 n=a+b+c+d,设 χ 2 = 𝒏(𝒂𝒅-𝒃𝒄) 𝟐 (𝒂+𝒃)(𝒄+𝒅)(𝒂+𝒄)(𝒃+𝒅)

任意给定一个α(称为显著性水平,通常取为0.05,0.01等),可以 找到满足条件Px≥)=a的数k(称为显著性水平a对应的分位 数).如果根据样本数据算出x的值后,发现≥k成立,就称在犯 错误的概率不超过α的前提下,可以认为A与B不独立(也称为 A与B有关);或说有1-的把握认为A与B有关若x2<k成立,就 称不能得到前述结论.这一过程通常称为独立性检验 (2)独立性检验通常得到的结果,或者是有1-α的把握认为A与 B有关,或者没有1-a的把握认为A与B有关
导航 任意给定一个α(称为显著性水平,通常取为0.05,0.01等),可以 找到满足条件P(χ 2≥k)=α的数k(称为显著性水平α对应的分位 数).如果根据样本数据算出χ 2的值后,发现χ 2≥k成立,就称在犯 错误的概率不超过α的前提下,可以认为A与B不独立(也称为 A与B有关);或说有1-α的把握认为A与B有关.若χ 2<k成立,就 称不能得到前述结论.这一过程通常称为独立性检验. (2)独立性检验通常得到的结果,或者是有1-α的把握认为A与 B有关,或者没有1-α的把握认为A与B有关
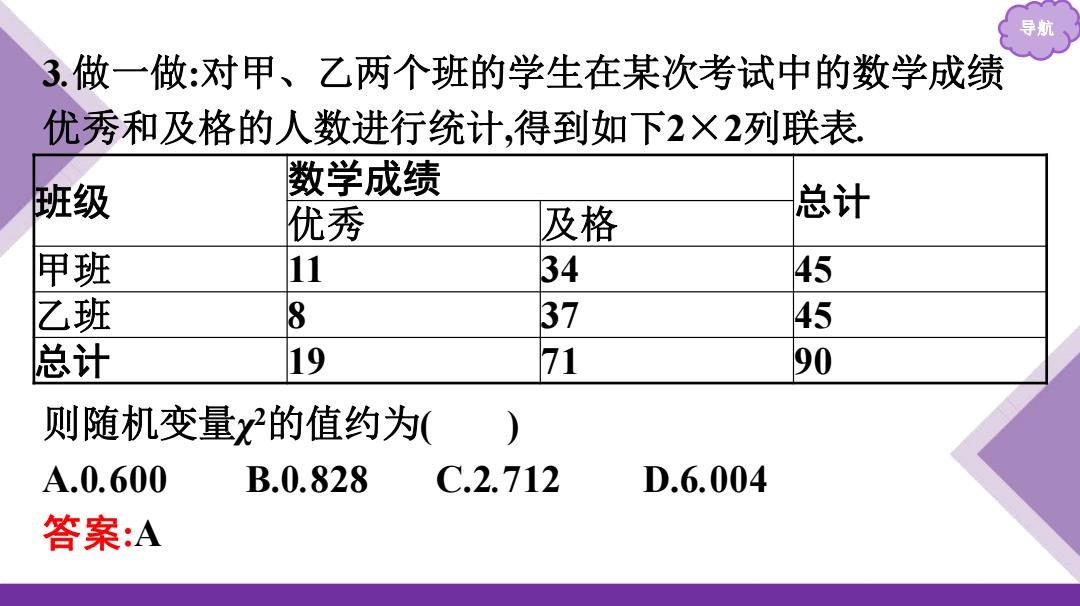
导则 3.做一做:对甲、乙两个班的学生在某次考试中的数学成绩 优秀和及格的人数进行统计,得到如下2×2列联表, 班级 数学成绩 优秀 及格 总计 甲班 11 34 45 乙班 8 37 45 总计 19 71 90 则随机变量x的值约为( A.0.600 B.0.828 C.2.712 D.6.004 答案:A
导航 3.做一做:对甲、乙两个班的学生在某次考试中的数学成绩 优秀和及格的人数进行统计,得到如下2×2列联表. 班级 数学成绩 总计 优秀 及格 甲班 11 34 45 乙班 8 37 45 总计 19 71 90 则随机变量χ 2的值约为( ) A.0.600 B.0.828 C.2.712 D.6.004 答案:A

导航 解析:根据2×2列联表中的数据,可得 X-90x1x37382≈0.60,故选A. 45×45×19×71
导航 解析:根据 2×2 列联表中的数据,可得 χ 2 = 𝟗𝟎×(𝟏𝟏×𝟑𝟕-𝟑𝟒×𝟖) 𝟐 𝟒𝟓×𝟒𝟓×𝟏𝟗×𝟕𝟏 ≈0.600.故选 A

导 【思考辨析】 判断下列说法是否正确,正确的在它后面的括号里画“√”,错 误的画“X” (1)2×2列联表中的数据是两个事件的频数.( (2)事件A与B无关,即两个事件互不影响.( 3)x的大小是判断事件A与B是否相关的统计量.(
导航 【思考辨析】 判断下列说法是否正确,正确的在它后面的括号里画“√”,错 误的画“×” . (1)2×2列联表中的数据是两个事件的频数.( √ ) (2)事件A与B无关,即两个事件互不影响.( √ ) (3)χ 2的大小是判断事件A与B是否相关的统计量.( √ )