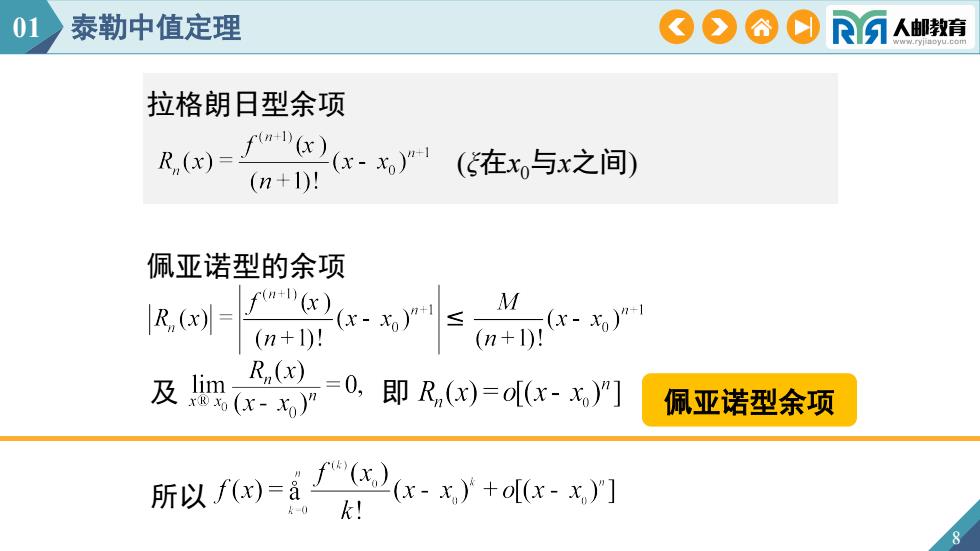
01泰勒中值定理COAORA人邮教育拉格朗日型余项n+1)xR,(x)x.)n+(在xo与x之间)(n+I)!佩亚诺型的余项Mr(n+)(xR, (x)(n +1)!(n + I)!R,(x)lim0.及即 R,(x)=o[(x- x)"]佩亚诺型余项XRXo(X-所以f(x)=a(x- x)"+o[(x- x)"]k!0
佩亚诺型余项 (ξ在x0与x之间) 拉格朗日型余项 佩亚诺型的余项 及 即 所以 01 泰勒中值定理 8

01泰勒中值定理CO0RA人邮教育fax))+L +"(x)f(x)= f(x)+ fdx)(x- x)(x- x)"+R(x)2!n!f(n+1)(x)R,(x) =(x- x)"*注(n +1)!1.当n=0时.泰勒公式变成拉格朗日中值公式f(xr)=f(xo)+ fdx)(x- xo) (在x与xo之间)2. 取x=0. 在0与x之间,令x =qx(0<q<1)则余项 R,(x)=u)(g)x-1(n+1)!3.当x=0 时,取x=qx(0<q<1),得麦克劳林公式
注 1. 当 时. 泰勒公式变成拉格朗日中值公式 3. 当 时, (ξ在x与x0之间) ξ在0与x之间, 则余项 2. 取 令 取 得麦克劳林公式. 01 泰勒中值定理 9

R人邮教育本讲内容W,nvlaDyu.c01泰勒中值定理02麦克劳林公式03几个重要初等函数的麦克劳林公式04泰勒公式的应用
01 泰勒中值定理 02 麦克劳林公式 03 几个重要初等函数的麦克劳林公式 04 泰勒公式的应用 本 讲 内 容

02麦克劳林公式COA0人邮教育RA定理3.7设函数f(x)在含有x=0的某个开区间(a,b)内具有直到(n+1)阶导数,则对任意xl (a,b)有f(x)=f(0)+ fα0)x+2() x2 ++(ax)xn+1 (0<g<1)(3.5)n!(n +1)!称为函数f(x)的n阶带拉格朗日型余项的麦克劳林公式(x)=f(0)+ fα0)+2()x2+L +f(n)(0)2xn+0(x") (3.6)21n!称为带佩亚诺余项的n阶麦克劳林公式
定理3.7 称为带佩亚诺余项的n阶麦克劳林公式. 设函数 在含有 的某个开区间 内具有直到 称为函数 的n阶带拉格朗日型余项的麦克劳林公式. (3.6) 阶导数,则对任意 有 (3.5) 02 麦克劳林公式 11