西安电子科技大学：《实用大众线性代数》课程PPT教学课件（MATLAB版）第2章 矩阵运算及其应用

多次线性变换等价于矩阵连乘 1=411x1+412X2+a3X3 ·设 y2=a21x+a22X2+a23X3 写成Y=AX x1=b41+b2t2 ·及 x2=b241+b22t2 写成X=BT x3=b3141+b32t2 则有： a11 a12 名 Y= =ABT a22

多次线性变换等价于矩阵连乘 • 设 写成Y=AX • 及 写成Ｘ=BT • 则有： 1 11 1 12 2 13 3 2 21 1 22 2 23 3 y a x a x a x y a x a x a x  = + +   = + + 1 11 1 12 2 2 21 1 22 2 3 31 1 32 2 x b t b t x b t b t x b t b t  = +   = +   = + 11 12 11 12 13 1 21 22 21 22 23 2 31 32 b b a a a t b b a a a t b b         = =               Y ABT

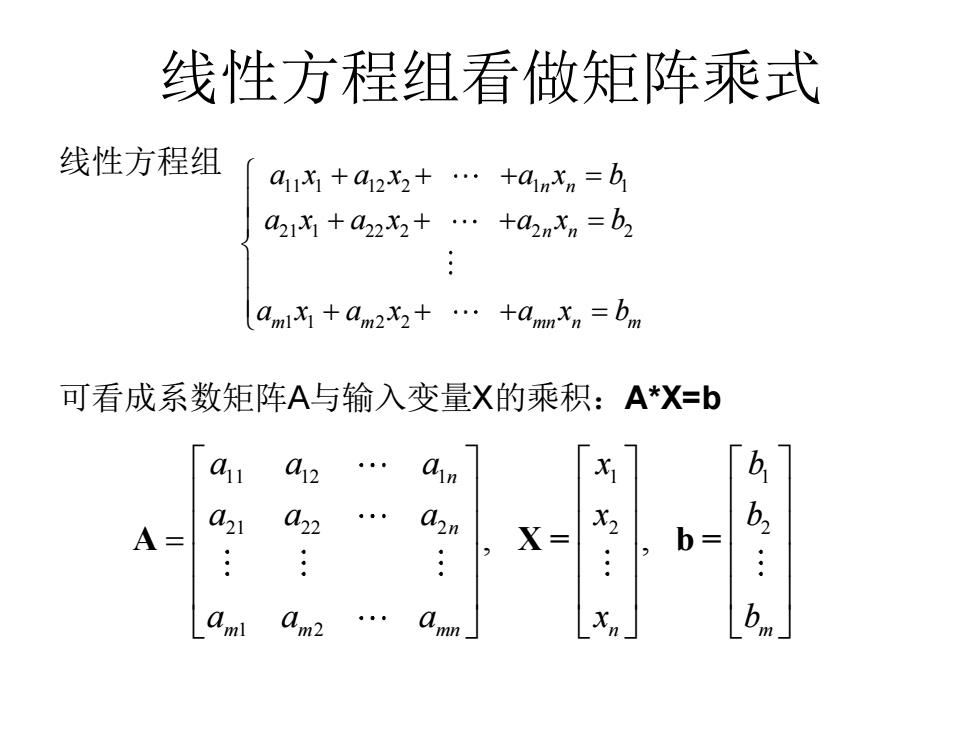
线性方程组看做矩阵乘式 线性方程组 411x1+a412X2+…+41mXn=b1 azx1 +a22x2+..+anxn =b2 amx+am2x2++amnxn =bm 可看成系数矩阵A与输入变量X的乘积：A*X=b a a12 n X A= 02 C22 02n X= b= b2 .: .: xn」

线性方程组看做矩阵乘式 线性方程组 可看成系数矩阵A与输入变量X的乘积：A*X=b 11 12 1 1 1 21 22 2 2 2 1 2 , , n n m m mn n m a a a x b a a a x b a a a x b             =                         A X = b = 11 1 12 2 1 1 21 1 22 2 2 2 1 1 2 2 n n n n m m mn n m a x a x a x b a x a x a x b a x a x a x b  + + + =   + + + =     + + + =

例2.6 [1 2-1 10 20 己知A= 3 4 0 ,B= -10 30 求AB和BA -2 5 6 -5 8 「1×10+2×(-10)+(-1)×(-5) 1×20+2×30+(-1)×8 ·AB 3×10+4×(-10)+0×(-5) 3×20+4×30+0×8 (-2)×10+5×(-10)+6×(-5)(-2)×20+5×30+6×8 -5 72 -10 180 -100158 ·BA不成立，因为内阶数不等，是非法运算

例2.6 • 已知 ， ，求AB和BA • AB • BA不成立，因为内阶数不等，是非法运算。 1 2 1 3 4 0 2 5 6   −   =       − A 10 20 10 30 5 8     = −      − B 1 10 2 ( 10) ( 1) ( 5) 1 20 2 30 ( 1) 8 3 10 4 ( 10) 0 ( 5) 3 20 4 30 0 8 ( 2) 10 5 ( 10) 6 ( 5) ( 2) 20 5 30 6 8    +  − + −  −  +  + −    =  +  − +  −  +  +        −  +  − +  − −  +  +  5 72 10 180 100 158   −   = −      −

4 例2.7 A=[1,2,31,B= 求AB和BA。 · 解A是1×3矩阵，B是3×1矩阵，矩阵A的列数等于矩 阵B的行数，所以A可以左乘B,乘积矩阵AB应该具有矩 阵A的行数，矩阵B的列数， 即是1×1矩阵： 4 AB=[1,2,3]5=1×4+2×5+3×6=32 6 ·当矩阵只有一行一列时，它退化为一个数，称为标量。 B是3×1矩阵，A是1X3矩阵，矩阵B的列数等于矩阵A 的行数，所以B也可以左乘A,乘积矩阵BA应该具有矩阵 B的行数，矩阵A的列数，即是3X3矩阵如下： 4 4×1 4×2 4×3 812 BA 5 1,2, 3]= 5×1 5×2 5×3 5 10 15 6×1 6×2 6×3 1218

例2.7 • 解 A是1 × 3矩阵，B是3 × 1矩阵，矩阵A的列数等于矩 阵B的行数，所以A可以左乘B，乘积矩阵AB应该具有矩 阵A的行数，矩阵B的列数，即是1 × 1矩阵： • 当矩阵只有一行一列时，它退化为一个数，称为标量。 • B是3 × 1矩阵，A是1 × 3矩阵，矩阵B的列数等于矩阵A 的行数，所以B也可以左乘A，乘积矩阵BA应该具有矩阵 B的行数，矩阵A的列数，即是3 × 3矩阵如下： • BA   4 1, 2, 3 , 5 , 6 AB BA     = =       A B 求 和 。   4 1, 2, 3 5 1 4 2 5 3 6 32 6     = =  +  +  =       AB  4 4 1 4 2 4 3 4 8 12 5 1, 2, 3 5 1 5 2 5 3 5 10 15 6 6 1 6 2 6 3 6 12 18                = =    =                      BA

矩阵乘法与标量乘法的不同 (1)矩阵乘法不满足交换律，即在一般情况下ABBA (2)不能由AB=0,推出A=0或B=0. 比如 A-3 却有AB=0, ·(3)不能由AC=AB,A0,推出B=C。上题若设C ,同样有AB=AC=0,但BC。 。 要注意，有些我们习惯的标量运算的公式，其中隐含地包 含了乘法交换律，这些公式在矩阵运算中也不能使用。如 (A+B)2≠A2+2AB+B2 (A+B)(A-B)≠A2-B2

矩阵乘法与标量乘法的不同 （1）矩阵乘法不满足交换律，即在一般情况下AB≠BA. （2）不能由AB=0，推出A=0或B=0. 比如 却有AB=0. • （3）不能由AC=AB,A≠0,推出B=C。上题若设 ，同样有AB=AC=0，但B≠C。 • 要注意，有些我们习惯的标量运算的公式，其中隐含地包 含了乘法交换律，这些公式在矩阵运算中也不能使用。如 2 4 2 , 1 2 1     = =         − − − A B 6 3   =   −   C   2 2 2 2 2 (A + B) A + 2AB + B (A + B)(A - B) A - B