
第二篇线性代数实践 第五章预备知识
第二篇 线性代数实践 第五章 预备知识

5.1实验在线性代数中的重要性 利用软件工具进行实验有以下的一些好处: o 好处一:对于低价(三阶及以下)的线性 代数问题,MATLAB能提供图形帮助,有利 于牢固地掌握概念。 。 好处二:对于高阶的问题,MATLAB能提供 计算程序,方便而简捷,节省时间。 好处三:由于解题快捷,在课程中可以较 多地放进线性代数的应用实例。扩展学生 的视野,提高学习的目的性和积极性
5.1 实验在线性代数中的重要性 利用软件工具进行实验有以下的一些好处: • 好处一:对于低价(三阶及以下)的线性 代数问题,MATLAB能提供图形帮助,有利 于牢固地掌握概念。 • 好处二:对于高阶的问题,MATLAB能提供 计算程序,方便而简捷,节省时间。 • 好处三:由于解题快捷,在课程中可以较 多地放进线性代数的应用实例。扩展学生 的视野,提高学习的目的性和积极性

“线性代数实践’的预期效果 所以我们敢于提出本书的标志性特征: 。 线性代数抽象吗?看了本书后,你会知道 它的概念都基于空间形象。 。 线性代数冗繁吗?学了本书后,你会懂得 它的计算全可有简明程序。 线性代数枯燥吗?读了本书后,你会发现 它的应用极其广泛又精彩
‘线性代数实践’的预期效果 所以我们敢于提出本书的标志性特征: • 线性代数抽象吗?看了本书后,你会知道 它的概念都基于空间形象。 • 线性代数冗繁吗?学了本书后,你会懂得 它的计算全可有简明程序。 • 线性代数枯燥吗?读了本书后,你会发现 它的应用极其广泛又精彩
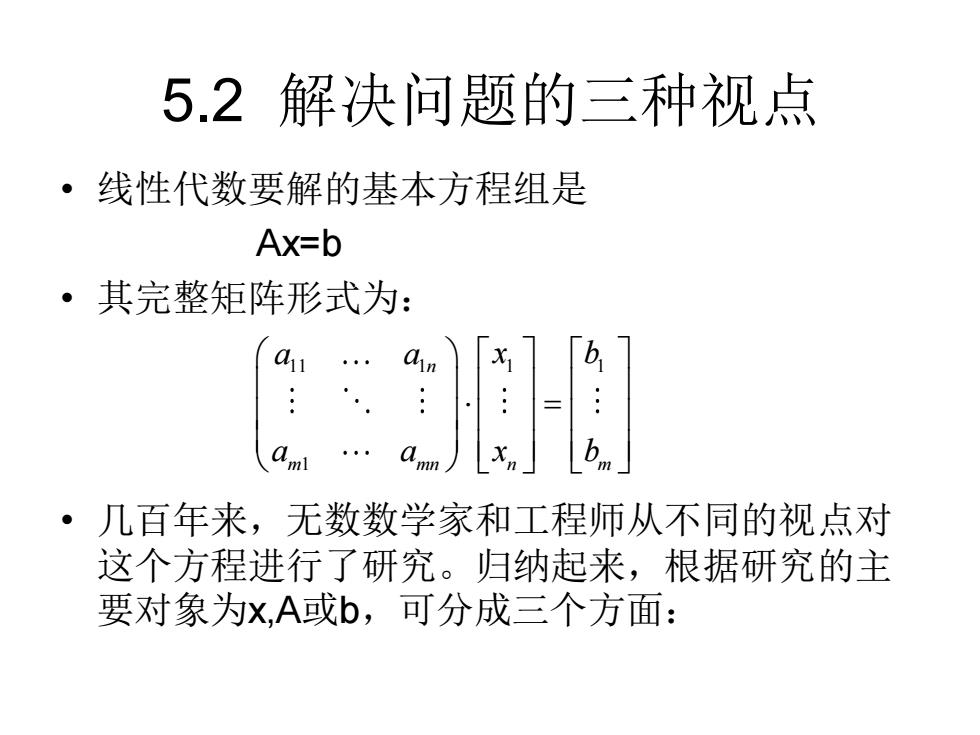
5.2解决问题的三种视点 ·线性代数要解的基本方程组是 Ax=b ·其完整矩阵形式为: am ·几百年来,无数数学家和工程师从不同的视点对 这个方程进行了研究。归纳起来,根据研究的主 要对象为x,A或b,可分成三个方面:
5.2 解决问题的三种视点 • 线性代数要解的基本方程组是 Ax=b • 其完整矩阵形式为: • 几百年来,无数数学家和工程师从不同的视点对 这个方程进行了研究。归纳起来,根据研究的主 要对象为x,A或b,可分成三个方面: 11 1 1 1 1 n m mn n m a a x b a a x b =

从解联立方程的视点 ·视点1:着重研究解x,即研究线性方程组的解法。 中学里做的就是这样,前面介绍的用MATLAB矩 阵除法的解也是如此。 要点:矩阵的每一行代表一个方程,m行代表m 个线性联立方程。n列代表n个变量。如果m是独 立方程数,根据m<n,m=n,m>n确定方程是’欠 定’、’适定’ 还是’超定’。对这三种情况都 会求解了,研究就完成了。 必须剔除非独立方程。.行阶梯形式、行列式和秩的 概念很大程度上为此目的而建立。 本书6,7两章对应于本视点,区别是第6章用行阶梯 变换(消元法)而第7章用矩阵运算
从解联立方程的视点 • 视点1:着重研究解x,即研究线性方程组的解法。 中学里做的就是这样,前面介绍的用MATLAB矩 阵除法的解也是如此。 要点:矩阵的每一行代表一个方程,m行代表m 个线性联立方程。 n列代表n个变量。如果m是独 立方程数,根据m<n,m=n,m>n确定方程是’欠 定’、’适定’还是’超定’。对这三种情况都 会求解了,研究就完成了。 必须剔除非独立方程。行阶梯形式、行列式和秩的 概念很大程度上为此目的而建立。 本书6,7两章对应于本视点,区别是第6章用行阶梯 变换(消元法)而第7章用矩阵运算