
第4章平面和空间向量 线性系统的许多重要特性可以用向量的概念来描 述,因为向量可以描述两个或两个以上的实数组 成的数组特征。二维和三维空间中的向量有鲜明 的几何意义,也有广泛的应用价值,掌握它们的 基本特性就可更好地从几何空间概念来理解线性 代数方程组的某些性质,同时也可帮助人们去抽 象推想高维的向量空间。,本章将介绍向量空间的 基本概念,用它来进一步诠释线性方程组的几何 意义;以便从几何概念过渡到代数推理,进而用 数学软件来解决它们的计算问题。下一章则讨论 二、三向量线性变换中一些较深入的问题
第4章 平面和空间向量 线性系统的许多重要特性可以用向量的概念来描 述,因为向量可以描述两个或两个以上的实数组 成的数组特征。二维和三维空间中的向量有鲜明 的几何意义,也有广泛的应用价值,掌握它们的 基本特性就可更好地从几何空间概念来理解线性 代数方程组的某些性质,同时也可帮助人们去抽 象推想高维的向量空间。本章将介绍向量空间的 基本概念,用它来进一步诠释线性方程组的几何 意义;以便从几何概念过渡到代数推理,进而用 数学软件来解决它们的计算问题。下一章则讨论 二、三向量线性变换中一些较深入的问题

4.1向量的类型 ·物理向量:向量这个术语起源于物理,用以表示既有大小 又有方向的物理量,如力,位移和速度等。那些只需用一 个实数来表示的物理量,如温度、压力和质量等就称为标 量。向量还可以有更广泛的意义,可以把任何由多个参数 描述的变量视为向量。如: ·1)一个班的学生本学期学了五门课,则每人的成绩就可 用五个分数组成的向量来反映; ·5).把人口按年龄分别统计可以得到一个具有100多维的 向量,如再按性别分开,得到的是200多维的向量。 。 不难看出,向量的引入极大地扩展了对象建模的深度和广 度
4.1 向量的类型 • 物理向量:向量这个术语起源于物理,用以表示既有大小 又有方向的物理量,如力,位移和速度等。那些只需用一 个实数来表示的物理量,如温度、压力和质量等就称为标 量。向量还可以有更广泛的意义,可以把任何由多个参数 描述的变量视为向量。如: • 1)一个班的学生本学期学了五门课,则每人的成绩就可 用五个分数组成的向量来反映; • … … • 5).把人口按年龄分别统计可以得到一个具有100多维的 向量,如再按性别分开,得到的是200多维的向量。 • 不难看出,向量的引入极大地扩展了对象建模的深度和广 度
几何向量和位置向量 ● 几何向量:把平面上 y 的向量的箭尾A的坐 标值取为(a1,a2),而 B (b1:62) 把箭头所处的点B的 坐标值取为(b1,b2), -◆Q(b1,a2) PP(b1-a1,b2-a2) 联接A点到B点的箭 A(a1,a2) 头就称为几何向量。 用v=AB示: 0 A称为向量的起点,而B称为向量的终点。这样的几何 向量,要用a1,a2,b1,b2四个实数才能表示。 把向量的箭尾A移到原点,箭头B就移到P点。这时的向 量作用线通过了原点,称为位置向量
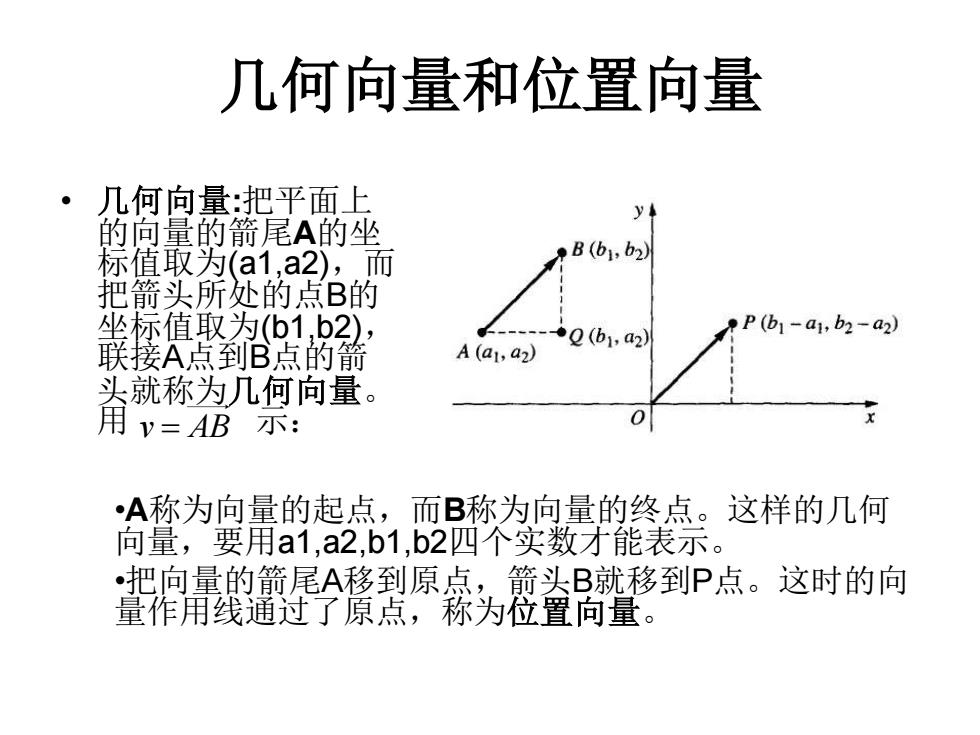
几何向量和位置向量 • 几何向量:把平面上 的向量的箭尾A的坐 标值取为(a1,a2),而 把箭头所处的点B的 坐标值取为(b1,b2), 联接A点到B点的箭 头就称为几何向量。 用 示: •A称为向量的起点,而B称为向量的终点。这样的几何 向量,要用a1,a2,b1,b2四个实数才能表示。 •把向量的箭尾A移到原点,箭头B就移到P点。这时的向 量作用线通过了原点,称为位置向量。 v AB =

代数向量 ·代数向量:把平面中的几何向量V用它在和y两个 方向的分量x和Vy来表示,写成表示式: ·这就是平面中用线性代数表示向量的方法。粗看 起来,它与几何向量的表示法没有太大的差别, 但到了三维以上,几何向量将失去意义,而代数 向量的维数可以无限地扩展,以满足工程和经济 模型分析的需要。从几何到代数,也就是从三维 向高维抽象的线性代数方法论
代数向量 • 代数向量:把平面中的几何向量v用它在x和y两个 方向的分量vx和vy来表示,写成表示式: • • 这就是平面中用线性代数表示向量的方法。粗看 起来,它与几何向量的表示法没有太大的差别, 但到了三维以上,几何向量将失去意义,而代数 向量的维数可以无限地扩展,以满足工程和经济 模型分析的需要。从几何到代数,也就是从三维 向高维抽象的线性代数方法论。 1 1 2 2 x y v b a v b a − = = − v

4.2向量及其线性组合 ·4.2.1平面和空间向量的矩阵表示 平面中的向量v用它在x和y两个方向的分量V1和v2来表示, 行向量写成v1,v2],列向量时为v= 为了节省 V 篇幅,有时按向量转置的规则,把列向量写成[V1,2]T。 ·例4.1设 ]{ 要求画出这两个向量的图形。 解:u和V都是二维空间的列向量。可以用平面坐标系中的 两个点,或从坐标原点引向这两点的箭头来表示
4.2 向量及其线性组合 • 4.2.1 平面和空间向量的矩阵表示 平面中的向量v用它在x和y两个方向的分量v1和v2来表示, 行向量写成[v1,v2],列向量时为 ,为了节省 篇幅,有时按向量转置的规则,把列向量写成[v1,v2]T 。 • 例4.1 设 要求画出这两个向量的图形。 解:u和v都是二维空间的列向量。可以用平面坐标系中的 两个点,或从坐标原点引向这两点的箭头来表示。 1 2 v v = v 1 1 2 2 2 3 , , 4 1 u v u v = = = = − u v