
真正讲透线性代数在二、三维空间的应用 ·工科线性代数现代化和大众化的思路之三 西安电子科技大学电子工程系陈怀琛 email:hchchen1934@vip.163.com 要:通过用线性代数对二三维向量空间进行分析和图解,使学生大大提高立体概念及其与线性变换 矩阵乘法及矩阵分解的关系。使得学习向量空间的概念更易接受并具有更强的实用性。 我在论文《论工科线性代数现代化和大众化》中曾经提出,对大学一年级的学生,能够 建立三维立体概念,己经是不低的要求了。其实教学计划中设立了好几门课程帮助达到这个 目的,如制图与画法几何,高等数学中的多变量微积分等,还有物理中的空间电磁场,数学 中的场论,电机课中的旋转磁场形成、乃至于信号处理中的复信号等等。线性代数也应该是 一个组成部分。我觉得至少对于弱电类的专业,实现的情况并不太好,学生的空间概念还是 很弱的,证据之一是许多学生,甚至部分毕业多年的教师,在后续课中,对频谱分析中的负 烦率,对信号处理中的复信号,都觉得难以理解。对机类专业而言,多自由度机器人,三坐 标测量仪,各种航行器在空间的运动,对线性代数在三维空间应用的要求更高。现有的线性 代数在此方面相当薄弱,很明显的 一点,就教材中使用的三维图形数目来比,中国教材往往 只有美国教材的10%以下,所以强化三维空间的概念是非常必要的。 一、 用二、三维向量来说明向量空间的运算规则 二维空间(平面)上的向量及其运算规则,特别是两个线性无关向量的线性组合是学生 理解线性代数的感性基础。MT的教材从下图讲向量的加减运算规则,进而列出其线性组 =[ +=[] 0 十十十 *-[+[]- -=-]-[8 图!向量的相加与相诚 合b=W+N=,再进一步的问题是平面上的任何向量b是否都能由这个线性组合 实现,其至设计了给定b猜测c,d的比赛,看谁能估计出最接近的c,d值。从这里又引入了 线性相关的概念,超定方程的概 (若b不在y平面上)等 从二维向量引深至三维向量和三维空间,并讨论向量的长度(范数)、向量的数量积(美 国的书上还喜欢用点乘(dot product)这个名词,MATLAB中也有点乘算符)、向量积和混合 积等。这时就有了更多的空间概念和图形。比如图2那样的图形
1 真正讲透线性代数在二、三维空间的应用 ——工科线性代数现代化和大众化的思路之三 西安电子科技大学电子工程系 陈怀琛 email: hchchen1934@vip.163.com 摘要:通过用线性代数对二三维向量空间进行分析和图解,使学生大大提高立体概念及其与线性变换、 矩阵乘法及矩阵分解的关系。使得学习向量空间的概念更易接受并具有更强的实用性。 我在论文《论工科线性代数现代化和大众化》中曾经提出,对大学一年级的学生,能够 建立三维立体概念,已经是不低的要求了。其实教学计划中设立了好几门课程帮助达到这个 目的,如制图与画法几何,高等数学中的多变量微积分等,还有物理中的空间电磁场,数学 中的场论,电机课中的旋转磁场形成、乃至于信号处理中的复信号等等。线性代数也应该是 一个组成部分。我觉得至少对于弱电类的专业,实现的情况并不太好,学生的空间概念还是 很弱的,证据之一是许多学生,甚至部分毕业多年的教师,在后续课中,对频谱分析中的负 频率,对信号处理中的复信号,都觉得难以理解。对机类专业而言,多自由度机器人,三坐 标测量仪,各种航行器在空间的运动,对线性代数在三维空间应用的要求更高。现有的线性 代数在此方面相当薄弱,很明显的一点,就教材中使用的三维图形数目来比,中国教材往往 只有美国教材的 10%以下,所以强化三维空间的概念是非常必要的。 一、 用二、三维向量来说明向量空间的运算规则 二维空间(平面)上的向量及其运算规则,特别是两个线性无关向量的线性组合是学生 理解线性代数的感性基础。MIT 的教材从下图讲向量的加减运算规则,进而列出其线性组 合 4 2 2 c d c d c d − + b v w = + = 。再进一步的问题是平面上的任何向量 b 是否都能由这个线性组合 实现,甚至设计了给定 b 猜测 c,d 的比赛,看谁能估计出最接近的 c,d 值。从这里又引入了 线性相关的概念,超定方程的概念(若 b 不在 xy 平面上)等。 从二维向量引深至三维向量和三维空间,并讨论向量的长度(范数)、向量的数量积(美 国的书上还喜欢用点乘(dot product)这个名词,MATLAB 中也有点乘算符)、向量积和混合 积等。这时就有了更多的空间概念和图形。比如图 2 那样的图形。 图 1 向量的相加与相减

而后在讲行列式的时候,又可以拿出图3的平行六面体说明三阶行列式的几何意义。 +,n+为.+ 图2三维空间的向量相加(左)和向量混合积(右) 人们都说线性代数是在几何与代数 之间建立的一座桥梁。所以把空间解析 几何放到线性代数中合并实施已经成为 许多学校的教学改革措施。几何是要用 图形说明概念的,线性代数既然作为桥 梁,必然要把图形,特别是三雏立体图 形放在特别重要的地位,把图形与代数 的表述与推导紧密结合,才能使学生理 (d1.a12.a13)← 解线性代数的方法论。线性代数的大众 化必须把这 点放在重要地位 而要做 到这一条,必须使对二三维向量空间的 图3三阶行列式等价于此平行六面体的体积 讨论在教材中占主要篇幅。如果突出N 维向量空间,那就必然扩大了公式推导的篇幅,图形就没有地位了! 用向量空间概念求超定方程组的好 用向量空间的方法往往可以更为简捷地推导公式,超定方程组的解可以作为一个例了 通常采用的是误差平方和最小的准则,其解也称为最小二乘解。国外所有作为公共课的线性 代数教材,都要讲这个内容,国内教材则几乎避开它。其实线性方程组只有适定、超定和欠 定三类,工程中要解决的只有前两类(因为欠 定方程属于条件不全的命题,工程师可以拒馅 12 解),不教学生解超定方程,等于浪费了线性 代数一半的功能。要严格地推导出最小二乘 的公式,利用空间几何概念是最方使而清楚 的。 在图1例中如果设b=5,10,求c,d,则可 4c-d=5 以得出以下的联立方程 2c+2ds10'解 c=2,d3。这是适定方程的情况其图形如右。 如果给出的是三维空间的b向量
2 而后在讲行列式的时候,又可以拿出图 3 的平行六面体说明三阶行列式的几何意义。 人们都说线性代数是在几何与代数 之间建立的一座桥梁。所以把空间解析 几何放到线性代数中合并实施已经成为 许多学校的教学改革措施。几何是要用 图形说明概念的,线性代数既然作为桥 梁,必然要把图形,特别是三维立体图 形放在特别重要的地位,把图形与代数 的表述与推导紧密结合,才能使学生理 解线性代数的方法论。线性代数的大众 化必须把这一点放在重要地位。而要做 到这一条,必须使对二三维向量空间的 讨论在教材中占主要篇幅。如果突出 N 维向量空间,那就必然扩大了公式推导的篇幅,图形就没有地位了! 二、 用向量空间概念求超定方程组的解 用向量空间的方法往往可以更为简捷地推导公式,超定方程组的解可以作为一个例子。 通常采用的是误差平方和最小的准则,其解也称为最小二乘解。国外所有作为公共课的线性 代数教材,都要讲这个内容,国内教材则几乎避开它。其实线性方程组只有适定、超定和欠 定三类,工程中要解决的只有前两类(因为欠 定方程属于条件不全的命题,工程师可以拒绝 解),不教学生解超定方程,等于浪费了线性 代数一半的功能。要严格地推导出最小二乘解 的公式,利用空间几何概念是最方便而清楚 的。 在图 1 例中如果设 b=[5;10],求 c,d,则可 以得出以下的联立方程: 4 5 2 2 10 c d c d − = + = ,解得 c=2,d=3。这是适定方程的情况其图形如右。 如 果 给 出 的 是 三 维 空 间 的 b 向 量 图 2 三维空间的向量相加(左)和向量混合积(右) 图 3 三阶行列式等价于此平行六面体的体积 0 5 10 -2 0 2 4 6 8 10 12 w 2w v 3v b=3w+2v
b=[5,101],那么,由于 「4「- w- 2v= 2 ,联立方程将成 00 4c-d=5 为:2c+2d=10。由于wv都在 0c+0d=1 y平面上,它们的线性组合绝不能 0.5 跑到0以外的空间位置去,故而 第三个方程是矛盾方程。 品木一垂解不要求方程左 2 0 的合成向量bb准确地等于 b,而是 要求它与b的误差e在平面上所有 图3简单情况下最小二乘解的几何意义 可能的bb中达到最小,在图上可 以看出,最小的误差即b的矢端离y平面的垂直距离,也就是应该从b的矢端向xy作的 垂线的长度。 如果v和w不在y平面上,那么最小二乘误差e的特征就应该是与v和w组成的平面 垂直,也就是与v和w都满足正交条件。ve=O,wIe=0,合成一个向量式: Are-fwi] =0,。因为e=b-bb,其中b是给定的方程组右端列向量,bb则是基本向 v 量的线性组合bb=cw+,其中c,d是待求的常数向量x的分量,通常我们用向量x上加 个帽x来表示,wv又组成系数矩阵A,于是bb=Ax,e-b-A,代入两个正交条件,经 过如下推导AT(b-A)=0,一ATAR=Ab一=(ATA)尸Ab,就得到了二三 阶条件下最小二乘解的公式。 设A为mxn矩阵,方程数m大于变量数n,称Ax=b为超定方程,即不可能找到一个 x,满足Ax-b=0。如果我们不寻求理想的数学解,而是从工程意义上找到尽量接近理想的 解,那就应该容许引入误差向量e。 e=Ax-b 其矩阵形式如下 能把误差向量的范数最小的x就定义为这个超定方程的最小二乘解,也称为×的估计 值,通常用立表示。 文=(ATA)ATb 3
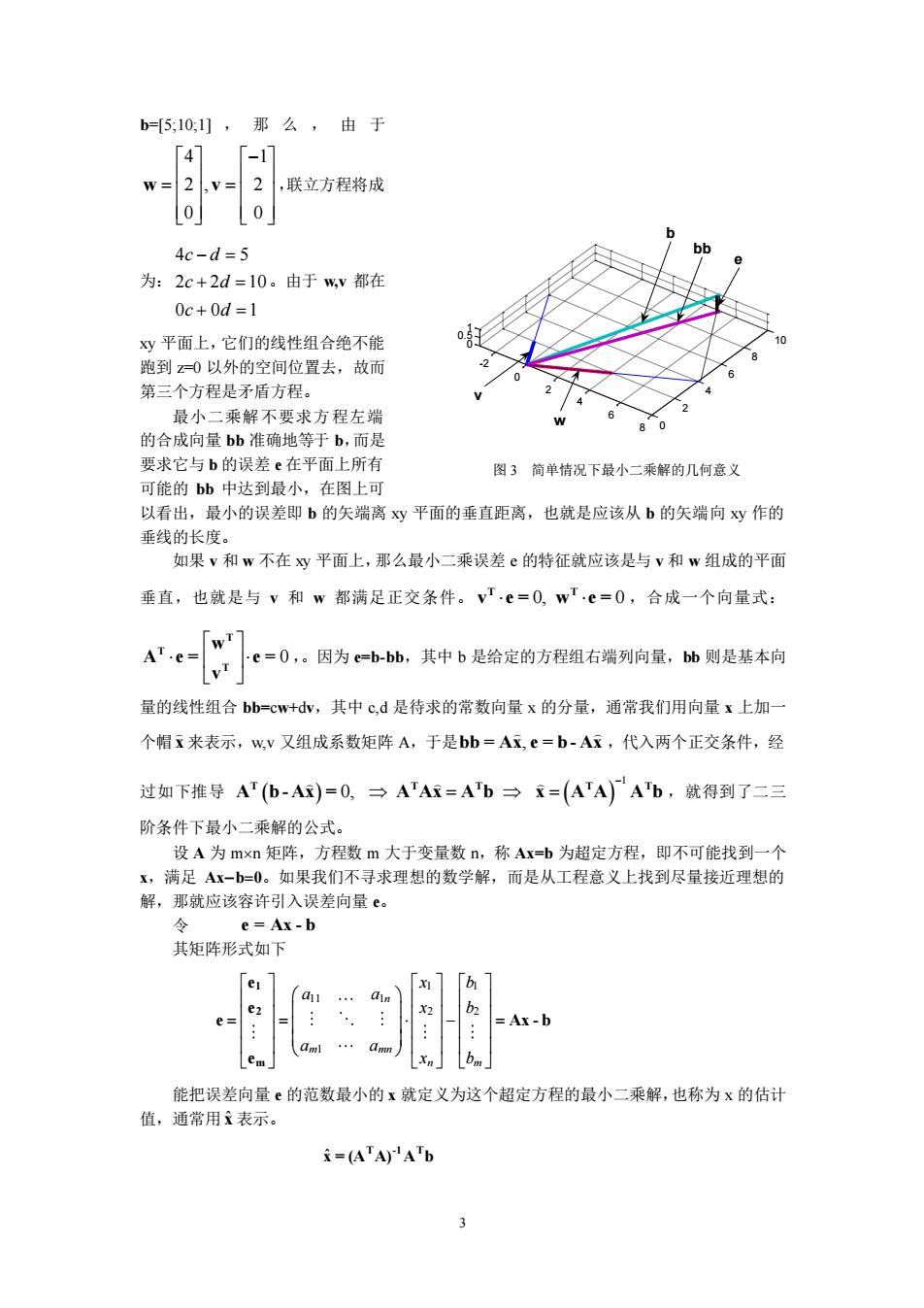
3 b=[5;10;1] ,那么,由于 4 1 2 , 2 0 0 − = = w v ,联立方程将成 为: 4 5 2 2 10 0 0 1 c d c d c d − = + = + = 。由于 w,v 都在 xy 平面上,它们的线性组合绝不能 跑到 z=0 以外的空间位置去,故而 第三个方程是矛盾方程。 最小二乘解不要求方程左端 的合成向量 bb 准确地等于 b,而是 要求它与 b 的误差 e 在平面上所有 可能的 bb 中达到最小,在图上可 以看出,最小的误差即 b 的矢端离 xy 平面的垂直距离,也就是应该从 b 的矢端向 xy 作的 垂线的长度。 如果 v 和 w 不在 xy 平面上,那么最小二乘误差 e 的特征就应该是与 v 和 w 组成的平面 垂直,也就是与 v 和 w 都满足正交条件。 0, 0 T T v e = w e = ,合成一个向量式: 0 T T T w A e = e = v ,。因为 e=b-bb,其中 b 是给定的方程组右端列向量,bb 则是基本向 量的线性组合 bb=cw+dv,其中 c,d 是待求的常数向量 x 的分量,通常我们用向量 x 上加一 个帽 x 来表示,w,v 又组成系数矩阵 A,于是 bb = Ax e = b - Ax , ,代入两个正交条件,经 过如下推导 ( ) ( ) 1 0, − = = T T T T T A b - Ax = A Ax A b x A A A b ,就得到了二三 阶条件下最小二乘解的公式。 设 A 为 mn 矩阵,方程数 m 大于变量数 n,称 Ax=b 为超定方程,即不可能找到一个 x,满足 Ax−b=0。如果我们不寻求理想的数学解,而是从工程意义上找到尽量接近理想的 解,那就应该容许引入误差向量 e。 令 e = Ax - b 其矩阵形式如下 1 1 11 1 2 2 1 n m mn n m x b a a x b a a x b = = − = 1 2 m e e e Ax - b e 能把误差向量 e 的范数最小的 x 就定义为这个超定方程的最小二乘解,也称为 x 的估计 值,通常用 x ˆ 表示。 ˆ T -1 T x = (A A) A b -2 0 2 4 6 8 0 2 4 6 8 10 0 0.5 1 e v w b bb 图 3 简单情况下最小二乘解的几何意义

由于在推导过程中并未有任何一步对维数有过限制,这个公式在高维的线性代数方程中 同样适用。 在MAAB中,把运算(ATA)-IAT单独编成一个子程序,称为piv函数,它是 Psuedoinverse(伪逆或广义逆)的缩称。这样,求最小二乘解的公式可以写成:x=pinv(A)b, MATLAB把左除求解的符号x=Ab通用于适定、欠定和超定三种情况,系统会自动根据系 数矩阵A的维数n和m进行判断而得出适当的解,读者必须对这些解能作出正确的判读, 因此对于三种方程的解的特性要有清楚的概念 三、 QR分解及施密特正交系的几何意义 从下面的例题开始,先考虑二阶的问题。设两个列向量v1=(1:2),v2一(6:8),组成向量组: A-l=[16 ,作QR分解:A=QR= T-0.44720.89447[2.23614.4721 28 0.89440.4472 08.9443 在笛卡尔坐标系中画出列向量v1,v2如图3a,Q满足正交向量组的条件QQ=。它的两个 Q,1) Q:,2)是长度为 的单位向量 5 画出了它们的方向。R则是向量v1,v2在新坐 216.8 1 标系中的坐标值。它的第一列只有一个元素说 明新坐标系的第一根轴取的就是v1方向.第 根轴则按正交分解的要求取的是与v1 11,2) 方向。QR分解实际 上仅仅对 换,从原来的笛卡尔正交坐标系转到新的正交 坐标系。两者之间仅仅是转动了一个角度0, 图3a两维矩阵QR分解的几何意义 其实Q就是按0 cose -sine 与0关联的 gin月cosa 新坐标系的特点是其第一根轴沿着第一根向量,它不改变描述对象(此处是v山,2向量组) 的形状和大小。如果两个向量v1,v2调换一下位置,Q和日都会发生改变,因为这时新坐标 系的第一根轴将取为2的方向。 现在来看三维向量的情况,设三个列向量v1=(9-5,2,v2=0,7,5),v3(-1:-9,句,组成向量 组A:用MATLAB语句Q,R=qA)作QR分解后,得到: 0017 08581024750.4499 1048812383745766 0-826552.6727 0.1907065990.7267 094822 同样可以检验QQ=,说明Q是归一化的三维空间正交坐标系,R中第一个列向量只 有个元素,说明新坐标的第一根轴取的是v1方向:R中第二个列向量有两个元素,说明 新坐标的第二根轴是取在v1,v2平面上,方向与v1正交:它的 三个列向量有三个元素 说明它在新坐标系的 向都有分量。因为在立体图中画出三个列向量和 根新坐标轴不 太容易,画出来了也看不清楚,此处就不画了。 y 四、工程中需用QR分解的实例 点1 -0.28 -0.03 0.55 点2 4.04459 3.01 工程中很多情况都需要建立新的坐标系,绝大部 分是正交坐标系。各种航行器(飞机、汽车、船舶、 点30720.71 -0.13 航天器)都要有自己的机身坐标系。它们与地面笛卡 点42.72 42L 6.23 尔坐标系的关系通常用三个空间角(欧拉角)来度量 点51.97181-032
4 由于在推导过程中并未有任何一步对维数有过限制,这个公式在高维的线性代数方程中 同样适用。 在 MATLAB 中,把运算(ATA)−1AT 单独编成一个子程序,称为 pinv 函数,它是 Psuedoinverse(伪逆或广义逆)的缩称。这样,求最小二乘解的公式可以写成:x=pinv(A)* b, MATLAB 把左除求解的符号 x=A\b 通用于适定、欠定和超定三种情况,系统会自动根据系 数矩阵 A 的维数 n 和 m 进行判断而得出适当的解,读者必须对这些解能作出正确的判读, 因此对于三种方程的解的特性要有清楚的概念。 三、 QR 分解及施密特正交系的几何意义 从下面的例题开始,先考虑二阶的问题。设两个列向量 v1=(-1;2),v2=(6;8),组成向量组: 1 6 2 8 − = A = v , v 1 2 ,作 QR 分解: -0.4472 0.8944 2.2361 4.4721 0.8944 0.4472 0 8.9443 = A = QR 。 在笛卡尔坐标系中画出列向量 v1,v2 如图 3a,Q 满足正交向量组的条件 QTQ=I2。它的两个 列向量 Q(:,1)和 Q(:,2)是长度为 1 的单位向量, 它们代表了新建立的坐标系 x1 和 y1,在图中 画出了它们的方向。R 则是向量 v1,v2 在新坐 标系中的坐标值。它的第一列只有一个元素说 明新坐标系的第一根轴取的就是 v1 方向,第二 根轴则按正交分解的要求取的是与 v1 正交的 方向。QR 分解实际上仅仅是一个正交坐标变 换,从原来的笛卡尔正交坐标系转到新的正交 坐标系。两者之间仅仅是转动了一个角度 θ, 其实 Q 就是按 cos sin sin cos − = Q 与 θ 关联的: 新坐标系的特点是其第一根轴沿着第一根向量,它不改变描述对象(此处是 v1,v2 向量组) 的形状和大小。如果两个向量 v1,v2 调换一下位置,Q 和 θ 都会发生改变,因为这时新坐标 系的第一根轴将取为 v2 的方向。 现在来看三维向量的情况,设三个列向量 v1=(9;-5;2),v2=(0;7;5),v3=(-1;-9;6),组成向量 组 A:用 MATLAB 语句[Q,R]=qr(A)作 QR 分解后,得到: 9 0 -1 -0.8581 -0.2475 -0.4499 -10.4881 2.3837 -4.5766 -5 7 -9 , 0.4767 -0.7094 -0.5191 , 0 -8.2655 2 5 6 -0.1907 -0.6599 0.7267 = = = A Q R 2.6727 0 0 9.4822 同样可以检验 QTQ=I3,说明 Q 是归一化的三维空间正交坐标系,R 中第一个列向量只 有一个元素,说明新坐标的第一根轴取的是 v1 方向;R 中第二个列向量有两个元素,说明 新坐标的第二根轴是取在 v1,v2 平面上,方向与 v1 正交;它的第三个列向量有三个元素, 说明它在新坐标系的三个方向都有分量。因为在立体图中画出三个列向量和三根新坐标轴不 太容易,画出来了也看不清楚,此处就不画了。 四、 工程中需用 QR 分解的实例 工程中很多情况都需要建立新的坐标系,绝大部 分是正交坐标系。各种航行器(飞机、汽车、船舶、 航天器)都要有自己的机身坐标系。它们与地面笛卡 尔坐标系的关系通常用三个空间角(欧拉角)来度量, x y z 点 1 -0.28 -0.03 0.55 点 2 4.04 4.59 3.01 点 3 0.72 0.71 -0.13 点 4 2.72 4.21 6.23 点 5 1.97 1.81 -0.32 -10 -5 0 5 10 -10 -5 0 5 10 x 1 y1 v1(-1,2) v2(6,8) 图 3a 两维矩阵 QR 分解的几何意义

这三个欧拉角又可以换算为3×3的方向余弦矩阵,通常也都是正交矩阵。机器人或机械手 的每一个关节的运动参数多数都是角度,这类新坐标系是建立在实体对象上。所以新的正交 坐标系的变换矩阵应该把重点放在旋 不必太强调以数据为基础的QR分解) Q分解要求以数据点为基准来建立新坐标系,下面 个较好的例子:数控坐标测量 仪测出某气红截面上五个点的X,V,z坐标如右表:问这五点是近似在一个平面上吗?离平面 有多大误弟?试写出该诉似平面的数学方程: 解:根据工件和夹具的状况,被测平面与笛卡尔坐标系早任意空间关系,所以从测得的 一个平面上。最好是建立一个新坐标系,使它的 y坐标与这些点所 在这个坐标系中各 点的z坐标 就可反映它们对平面的误差 (I)把五个数据点坐标作为列向量组,建立数据矩阵A。它应是3×5矩阵。 028004040007200272001g700 A=-0.03004.59000.71004.21001.8100 0.55003.0100-0130062300-0.3200 2)这些点的共面性反映为它们的差向量是否共面,首先求出这五个点之间的差向量 把点5选为基准,令DA为差距咋,则DA=A-A(,5)*one(I,5),它也是3X5矩阵。它的第 五列全为零,是零向量或新坐标的原点。 -2.25002.0700.1.25000.7500 DA= -184002.7800-1.10002.4000 0.87003.33000.19006.5500 0 (B)对DA作QR变换Q,R=qr(DA),就相当 -0.7416-0.09190.664 [3.03402.26621.6486-0.1335 0 Q=-0.6065-0.33160.7227 R= 0-4.23870.3012-7.0148 0 02868-0.93890.1902 000.00040.00990 可见在新的坐标系内,五个点有三个的z坐标为零,即新坐标系的y平面由1,2, 点确定,其余两个点的z坐标值也都在0.01以下,说明这五个点基本共面。其三维立体 图如下。 11.22473.1796x+12.1093.1796-1 图(回五个空间测量点及其拟合平面b)坐标旋转后使拟合平面看似成为一根线
5 这三个欧拉角又可以换算为 3×3 的方向余弦矩阵,通常也都是正交矩阵。机器人或机械手 的每一个关节的运动参数多数都是角度,这类新坐标系是建立在实体对象上。所以新的正交 坐标系的变换矩阵应该把重点放在旋转角上,不必太强调以数据为基础的 QR 分解方法。 QR 分解要求以数据点为基准来建立新坐标系,下面是一个较好的例子:数控坐标测量 仪测出某气缸截面上五个点的 x,y,z 坐标如右表:问这五点是近似在一个平面上吗?离平面 有多大误差?试写出该近似平面的数学方程; 解:根据工件和夹具的状况,被测平面与笛卡尔坐标系呈任意空间关系,所以从测得的 数据无法看出它是否在一个平面上。最好是建立一个新坐标系,使它 的 xy 坐标与这些点所 在的平面大体重合,在这个坐标系中各点的 z 坐标,就可反映它们对平面的误差。 (1)把五个数据点坐标作为列向量组,建立数据矩阵 A。它应是 3×5 矩阵。 -0.2800 4.0400 0.7200 2.7200 1.9700 -0.0300 4.5900 0.7100 4.2100 1.8100 0.5500 3.0100 -0.1300 6.2300 -0.3200 = A (2)这些点的共面性反映为它们的差向量是否共面,首先求出这五个点之间的差向量, 把点 5 选为基准,令 DA 为差距咋,则 DA=A-A(:,5)*ones(1,5),它也是 3×5 矩阵。它的第 五列全为零,是零向量或新坐标的原点。 -2.2500 2.0700 -1.2500 0.7500 0 -1.8400 2.7800 -1.1000 2.4000 0 0.8700 3.3300 0.1900 6.5500 0 = DA (3)对 DA 作 QR 变换[Q,R]=qr(DA),就相当于 -0.7416 -0.0919 0.6645 3.0340 -2.2662 1.6486 -0.1335 0 -0.6065 -0.3316 -0.7227 , 0 -4.2387 0.3012 -7.0148 0 0.2868 -0.9389 0.1902 0 = = Q R 0 0.0004 0.0099 0 可见在新的坐标系内,五个点有三个的 z 坐标为零,即新坐标系的 xy 平面由 1,2,5 三点确定,其余两个点的 z 坐标值也都在 0.01 以下,说明这五个点基本共面。其三维立体 图如下。 图 (a) 五个空间测量点及其拟合平面 (b)坐标旋转后使拟合平面看似成为一根线