西安电子科技大学：《实用大众线性代数》课程PPT教学课件（MATLAB版）第2章 矩阵运算及其应用

数乘的定义及运算规则 数λ与矩阵 的乘积，简称数乘，记作λA或AW, 规定为 A=(a) xn 2a11 2a12 九A=A几= 2a21 2d22 2C, Aa a 矩阵的加法和数乘统称为矩阵的线性运算，运算规律相同： (1)加法交换律：A+B=B+A (2)加法结合律：A+(B+C)=(A+B)+C (3)数乘结合律：（2)A=(uA)=(2A (4)数乘分配律 (A+B)=九A+B

数乘的定义及运算规则 数λ与矩阵 的乘积，简称数乘，记作λA或Aλ ， 规定为 矩阵的加法和数乘统称为矩阵的线性运算，运算规律相同： （1）加法交换律: A+B=B+A （2）加法结合律: A+(B+C)=(A+B)+C （3）数乘结合律： （4）数乘分配律 ( ij)m n a  A = 11 12 1 21 22 2 1 2 n n m m mn a a a a a a a a a                = =           A A(     ) A A A = = ( ) ( )    (A B A B + ) = +

矩阵的乘法 例2.3有甲、乙、丙、丁4个服装厂， 表2.5服装厂的月产量 一个月的产量情况由表2.5给出， 甲 乙 丙 丁 若甲厂生产8个月，乙厂生产10 个月，丙厂生产5个月，而丁厂生 帽 20 4 2 7 产9个月，则共生产帽子、衣服、 衣 10 18 6 裤子各多少？用矩阵来描述。 裤 5 7 16 3 8 20 77 10 A- 10 18 5 6 b= 5 J 7 16 3 9 20×8+4×10+2×5+7×9 273 C=A*b= 10×8+18×10+5×5+6×9 339 5×8+7×10+16×5+3×9 217

矩阵的乘法 例2.3 有甲、乙、丙、丁4个服装厂， 一个月的产量情况由表2.5给出， 若甲厂生产8个月，乙厂生产10 个月，丙厂生产5个月，而丁厂生 产9个月，则共生产帽子、衣服、 裤子各多少？用矩阵来描述。 表2.5 服装厂的月产量 甲 乙 丙 丁 帽 20 4 2 7 衣 10 18 5 6 裤 5 7 16 3 20 4 2 7 10 18 5 6 5 7 16 3     =       A 8 10 5 9     =           b 20 8 4 10 2 5 7 9 273 10 8 18 10 5 5 6 9 339 5 8 7 10 16 5 3 9 217      +  +  +      =  +  +  +  =              +  +  +  C = A * b

矩阵乘法定义 定义2.3设A是m×s矩阵，B是sXn矩阵，那么矩阵和矩阵的乘积 是一个m×n矩阵C,其中C的各个元素为： C=∑akbg=an4,+a2b2,+…+abg k=1 (2.1.3) (i=1,2,…,mj=1,2,…,n) ·记作C=A*B。称左矩阵的列数和右矩阵的行数s为内阶数，由定义 知，只有当它们的内阶数相等时，两个矩阵才能相乘。 a11 a2…4s … C Cui Cin .: W b2 a12 ais . Ci Cin … bsi am Cml Cmj ·Cmn 按定义，矩阵乘法不满足交换律

矩阵乘法定义 • 定义2.3 设A是m×s矩阵，B是s×n矩阵，那么矩阵和矩阵的乘积 是一个m×n矩阵C，其中C的各个元素为： • （2.1.3） • 记作C=A*B。称左矩阵的列数和右矩阵的行数s为内阶数，由定义 知，只有当它们的内阶数相等时，两个矩阵才能相乘。 按定义，矩阵乘法不满足交换律。 1 1 2 2 1 s ij ik kj i j i j is sj k c a b a b a b a b = = = + + +  (i m j n = = 1,2, , ; 1,2, , ) 11 12 1 11 1 1 11 1 1 21 2 2 1 2 1 1 1 1 1 s j n j n j n i i i s i i j i n s s j s n m m m s m m j m n a a a c c c b b b b b b a a a c c c b b b a a a c c c                   =                    

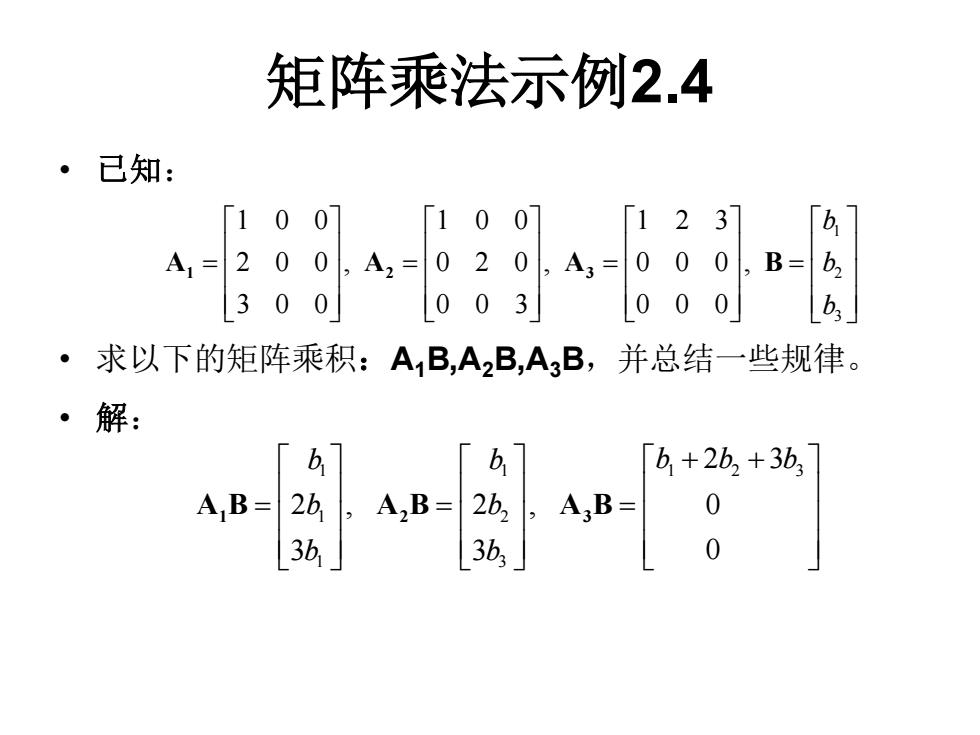
矩阵乘法示例2.4 ·已知： 「100 100 「123 「b A1=200, A2=020,A3= 0 0 0,B= b2 300 0 03 0 0 0 b3」 求以下的矩阵乘积：AB,A2B,A3B,并总结一些规律。 ·解： b b b+2b2+3b A,B=2b 1，A2B=1 0 [3b

矩阵乘法示例2.4 • 已知： • 求以下的矩阵乘积：A1B,A2B,A3B，并总结一些规律。 • 解： 1 2 3 1 0 0 1 0 0 1 2 3 2 0 0 , 0 2 0 , 0 0 0 , 3 0 0 0 0 3 0 0 0 b b b                 = = = =                         A A A B 1 2 3 1 1 1 2 3 1 2 1 3 2 3 2 , 2 , 0 3 3 0 b b b b b b b b b       + +       = = =                   A B A B A B 1 2 3

定义2.4 线性变换 ·对于向量Y=[y1,y2,,ym],若它们能由变量X=[x,x2,…,xn] 线性表示，即有： y=a+a2x2+.+ainxn y2=a21x1+a222+…+a2nXm (2.1.4) ym =amx +am2x2++amnxn 则称此关系式为变量X到变量Y的线性变换。可以写成输 出向量Y等于系数矩阵A左乘输入向量X: a11 a12 … an 21 Y= a22 02 =AX（2.1.5) ym am am2 Xn

定义2.4 线性变换 • 对于向量 ，若它们能由变量 线性表示，即有： （2.1.4） • 则称此关系式为变量Ｘ到变量Ｙ的线性变换。可以写成输 出向量Y等于系数矩阵A左乘输入向量X： （2.1.5） 1 11 1 12 2 1 2 21 1 22 2 2 1 1 2 2 n n n n m m m mn n y a x a x a x y a x a x a x y a x a x a x  = + + +   = + + +     = + + + 1 11 12 1 1 2 21 22 2 2 1 2 = n n m m m mn n y a a a x y a a a x y a a a x                   = =                         Y AX T m [ y , y , , y ] Y = 1 2  T n [x , x , , x ] X = 1 2 