
第5章线性变换及其特征 线性代数归根到底就是讨论方程组 Ax=b,只是采取不同的角度。本书前三 章是已知A和b求x,解的方法是以A的行 变换(也就是方程)为主;第四章则把A 的看作列向量组,把Ax看作列向量的线 性组合,研究其和是否能等于另一个向量 b。这一章则把A看作一个变换,把x域中 的图形或向量变换到b域(本章中看作y域) 中,要研究的是变换前后两个坐标系内的 图形和向量会有何种变化。这三个不同角 度反映了不同的对线性代数的应用需求, 也深化了对线性方程组的研究
第5章 线性变换及其特征 线性代数归根到底就是讨论方程组 Ax=b,只是采取不同的角度。本书前三 章是已知A和b求x,解的方法是以A的行 变换(也就是方程)为主;第四章则把A 的看作列向量组,把Ax看作列向量的线 性组合,研究其和是否能等于另一个向量 b。这一章则把A看作一个变换,把x域中 的图形或向量变换到b域(本章中看作y域) 中,要研究的是变换前后两个坐标系内的 图形和向量会有何种变化。这三个不同角 度反映了不同的对线性代数的应用需求, 也深化了对线性方程组的研究
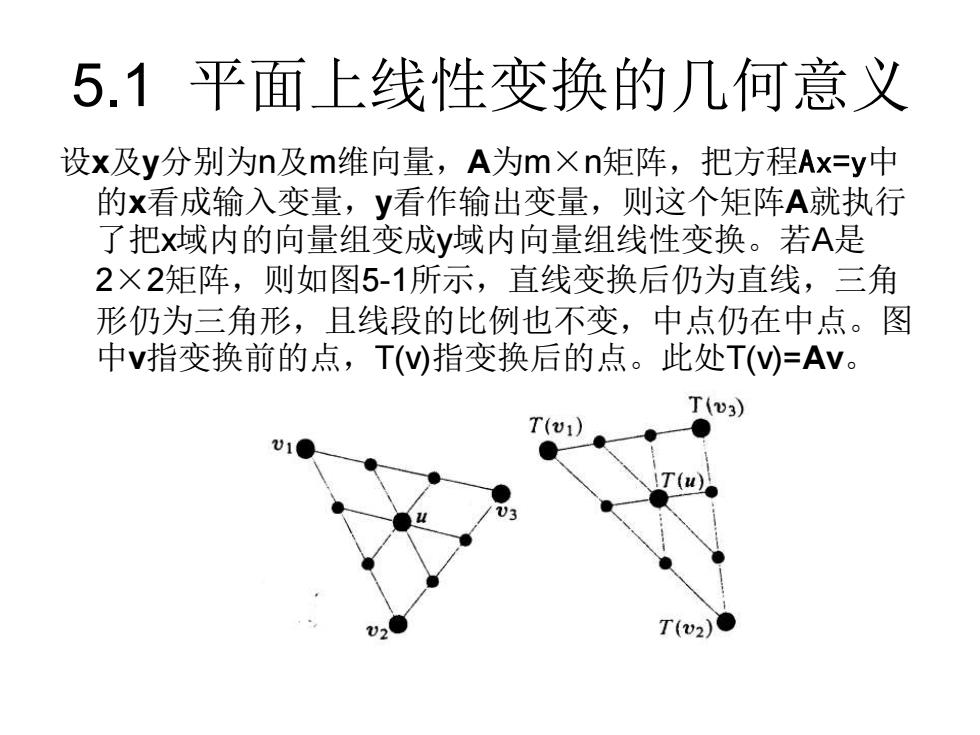
5.1平面上线性变换的几何意义 设x及y分别为n及m维向量,A为m×n矩阵,把方程Ax=y中 的x看成输入变量,y看作输出变量,则这个矩阵A就执行 了把x域内的向量组变成y域内向量组线性变换。若A是 2×2矩阵,则如图5-1所示,直线变换后仍为直线,三角 形仍为三角形,且线段的比例也不变,中点仍在中点。图 中v指变换前的点,T(W)指变换后的点。此处T(W=Av。 T(v3) T(v1) T(v2)
5.1 平面上线性变换的几何意义 设x及y分别为n及m维向量,A为m×n矩阵,把方程Ax=y中 的x看成输入变量,y看作输出变量,则这个矩阵A就执行 了把x域内的向量组变成y域内向量组线性变换。若A是 2×2矩阵,则如图5-1所示,直线变换后仍为直线,三角 形仍为三角形,且线段的比例也不变,中点仍在中点。图 中v指变换前的点,T(v)指变换后的点。此处T(v)=Av

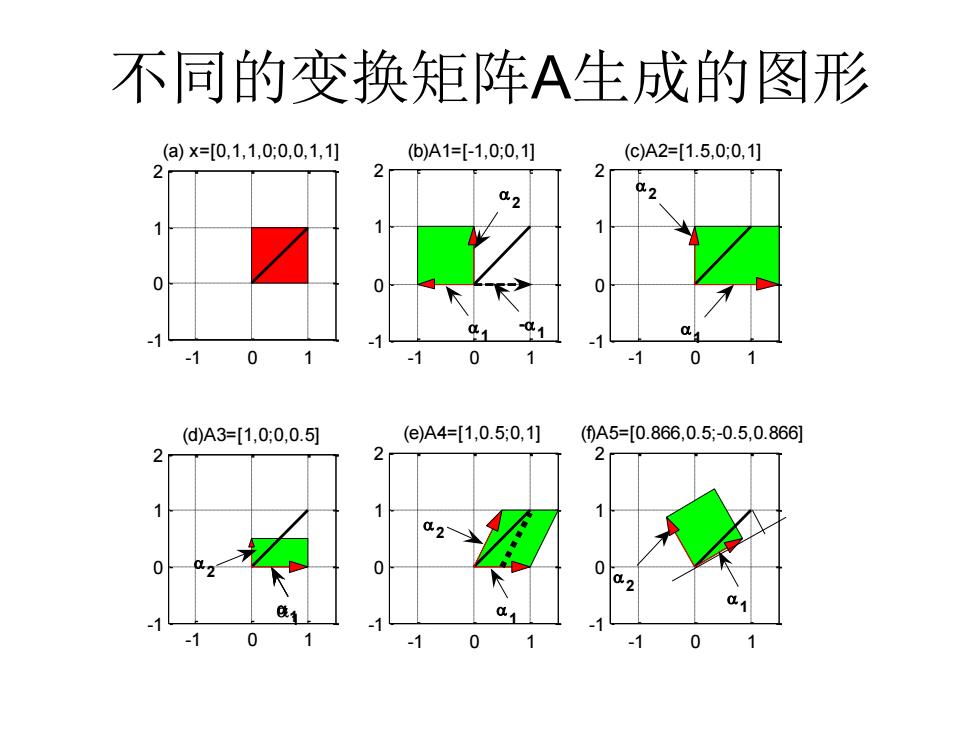
平面线性变换产生的图形示例 用本书pla501来完成计算和绘图,其核心语句如下。 X=[0,1,1,0;0,0,1,1];subplot(2,3,1),fl(x1,),0],[x(2,:),0],'r) axis equal,axis([-1.5,1.5,-1,2]),grid on A1=[-1,0;0,1],y1=A1*x,subplot(2,3,2),fly1(1,),0],y1(2,),0],'g) 这里把y2~y5的绘图语句中的坐标设置和标题语句都作了 省略,读者不难从y1的绘图语句推断。运行这个程序可以 得到前面列出的y1y5的值,它们与x一样都用2×5的矩阵 表示,同时得到图5-2所示的图形。可以看出,矩阵A1使 原图对纵轴生成镜像(反射),矩阵A2使原图在横轴方 向膨胀,矩阵A3使原图在纵轴方向压缩,矩阵A4使原图 向右上方剪切变形,矩阵A5使原图沿反时针方向旋转 t=pi/6
平面线性变换产生的图形示例 • 用本书pla501来完成计算和绘图,其核心语句如下。 • x=[0,1,1,0;0,0,1,1];subplot(2,3,1),fill([x(1,:),0],[x(2,:),0],'r') • axis equal,axis([-1.5,1.5,-1,2]),grid on • A1=[-1,0;0,1],y1=A1*x, subplot(2,3,2),fill([y1(1,:),0],[y1(2,:),0],'g') • …… • 这里把y2~y5的绘图语句中的坐标设置和标题语句都作了 省略,读者不难从y1的绘图语句推断。运行这个程序可以 得到前面列出的y1~y5的值,它们与x一样都用2×5的矩阵 表示,同时得到图5-2所示的图形。可以看出,矩阵A1使 原图对纵轴生成镜像(反射),矩阵A2使原图在横轴方 向膨胀,矩阵A3使原图在纵轴方向压缩,矩阵A4使原图 向右上方剪切变形,矩阵A5使原图沿反时针方向旋转 t=pi/6

不同的矩阵A产生的变换结果 例5.1设x为二维平面上的一个单位方块,其四个顶点为 (0,0),(1,0),(1,1),(0,1),加一个(0,0)。把不同的2×2矩阵A 左乘此组2×5数据矩阵,可以得到多种不同的图形。 (1) 10 A1= 1 )0110 y2= 1.5 1.5 0 0 (2) /0 0 1.0 1.0 Y3= 0 1.0 1.0 0 (3) 0.5 0.5 0 0 1.0 1.5 0.5 0 (4) A4= y4= 1.0 1.0 0 cos t -sin t 0 0.866 0.366-0.500 0 A5 (5) y5= sint cos t 0.500 1.366 0.866 0
不同的矩阵A产生的变换结果 例5.1 设x为二维平面上的一个单位方块,其四个顶点为 (0,0), (1,0), (1,1), (0,1),加一个(0,0)。把不同的2×2矩阵A 左乘此组2×5数据矩阵,可以得到多种不同的图形。 (1) (2) (3) (4) (5) 1 0 0 -1 -1 0 0 , 0 1 0 0 1 1 0 − = = A1 y1 1.5 0 0 1.5 1.5 0 0 , 0 1 0 0 1.0 1.0 0 = = A2 y2 1.0 0 0 1.0 1.0 0 0 , 0 0.5 0 0 0.5 0.5 0 = = A3 y3 1.0 0.5 0 1.0 1.5 0.5 0 , 0 1.0 0 0 1.0 1.0 0 = = A4 y4 cos t -sin t 0 0.866 0.366 -0.500 0 , sin t cos t 0 0.500 1.366 0.866 0 = = A5 y5
不同的变换矩阵A生成的图形 (a)x=[0,1,1,0:0,0,1,1] (b)A1=-1,0:0,1] (c)A2=[1.5,0:0,1] 02 0 0 0 0 (d)A3=[1,0:0,0.5] (e)A4=[1,0.5;0,1] (①A5=[0.866,0.5;-0.5,0.866] 2 2 0
不同的变换矩阵A生成的图形 -1 0 1 -1 0 1 2 (a) x=[0,1,1,0;0,0,1,1] -1 0 1 -1 0 1 2 (b)A1=[-1,0;0,1] -1 0 1 -1 0 1 2 (c)A2=[1.5,0;0,1] -1 0 1 -1 0 1 2 (d)A3=[1,0;0,0.5] -1 0 1 -1 0 1 2 (e)A4=[1,0.5;0,1] -1 0 1 -1 0 1 2 (f)A5=[0.866,0.5;-0.5,0.866] 1 2 1 2 1 2 1 2 1 2 - 1