
例2.用对称式及参数式表示直线 x+y+z+1=0 2x-y+3z+4=0 解题思路: 先找直线上一点: 再找直线的方向向量 HIGH EDUCATION PRESS 机动目录上页下页返回结束
例2.用对称式及参数式表示直线 机动 目录 上页 下页 返回 结束 先找直线上一点; 再找直线的方向向量. 解题思路:
二、线面间的位置关系 1.两直线的夹角 两直线的夹角指其方向向量间的夹角(通常取锐角) 设直线L,L,的方向向量分别为 i=(m1,n1,p1),S2=(m2,2,p2) 则两直线夹角0满足 3·西 coso ss mm2+nn2+pip2 m2+m2++n2"p2 HIGH EDUCATION PRESS 机动目录上页下页返回结束
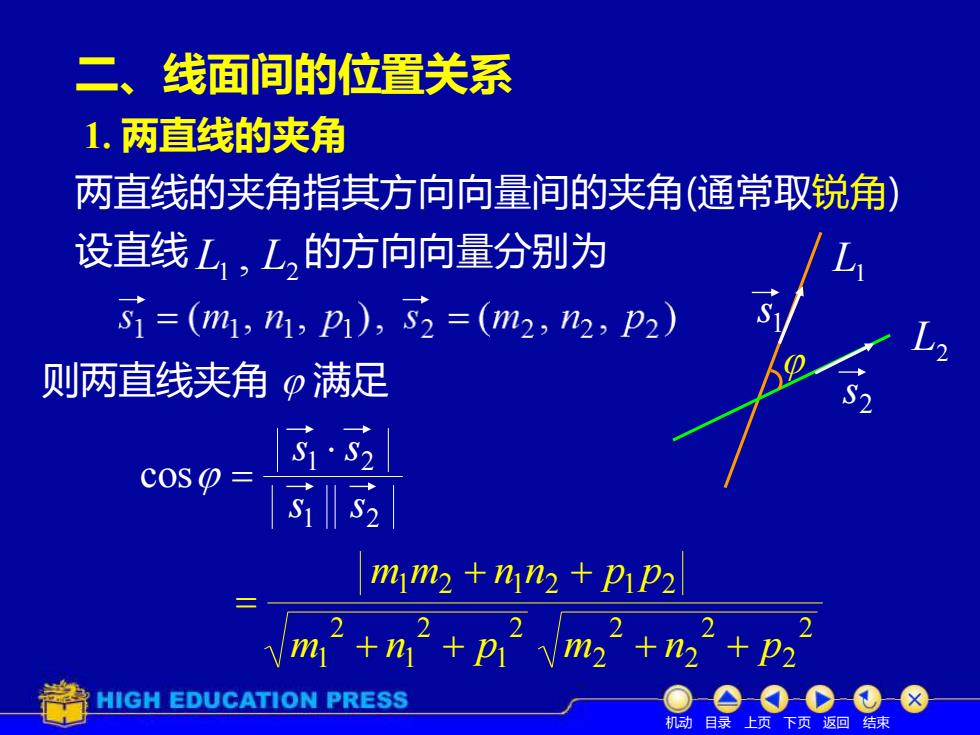
L2 L1 二、线面间的位置关系 1. 两直线的夹角 则两直线夹角 满足 1 2 设直线 L , L = 两直线的夹角指其方向向量间的夹角(通常取锐角) 的方向向量分别为 1 2 1 2 1 2 m m + n n + p p 2 1 2 1 2 m1 + n + p 2 2 2 2 2 m2 + n + p 1 2 1 2 cos s s s s = 1 s 2 s 机动 目录 上页 下页 返回 结束

特别有: (1)L1L2→了152→S52=0 > %m2+hn2+p1P2=0 (2)L/L2→/S2>s×52=0 %=%=D1 m2 n2 p2 HIGH EDUCATION PRESS 机动目录上页下页返回结束
特别有: 1 2 (1) L ⊥ L 1 2 (2) L // L m1m2 + n1n2 + p1 p2 = 0 2 1 2 1 2 1 p p n n m m = = 1 2 s ⊥ s 1 2 s //s 机动 目录 上页 下页 返回 结束 s1 s2 = 0 s1 s2 = 0