南阳师范学院：《高等数学》课程教学课件（同济第六版）第九章 多元函数微分法及其应用

例2设z=xy(x>0,且x≠1)，求证 x0z+1d2=22 yOx 证： =x 02 o 0x Oy x/Inx x 0z 1 0z yox Inxay =x+x'=22 例3求r=√x2+y2+z2 的偏导数 2x 解： ∂r 0x x-7 22+y2+z = ay r dz r

例2 设 y 且 xxxz  1,0( ）， z y z xx z y x 2 ln 1       证 :    x z  y z xx z y x       ln 1 例3 求 222  zyxr 的偏导数. 解 :    x r    y r yy  x  x    y z 求证 , y  1 xy xx y ln  2 z 222 2  zyx 2 x r x  r z z r    , r y

例4.已知理想气体的状态方程p/=RT(R为常数)， 求证： op ov aM=-1 av ar ap RT op RT 证：p= V av v2 说明：此例表明，偏导 V= RT aV R 数记号是一个整体记号， aT p 不能看作分子与分母的 T= OT V 商！ R’Op R ap av oT_ RT av Or py =-1 op

例4.已知理想气体的状态方程 求证:  1         p T T V V p Vp  R T 证: , V R T p  , p R T V  , R p V T            p T T V V p ( R为常数) ,    V p 2 V R T     T V p R    p T R V Vp R T    1 数记号是一个 说明: 不能看作分子与分母的 商 ! 此例表明,偏导 整体记号

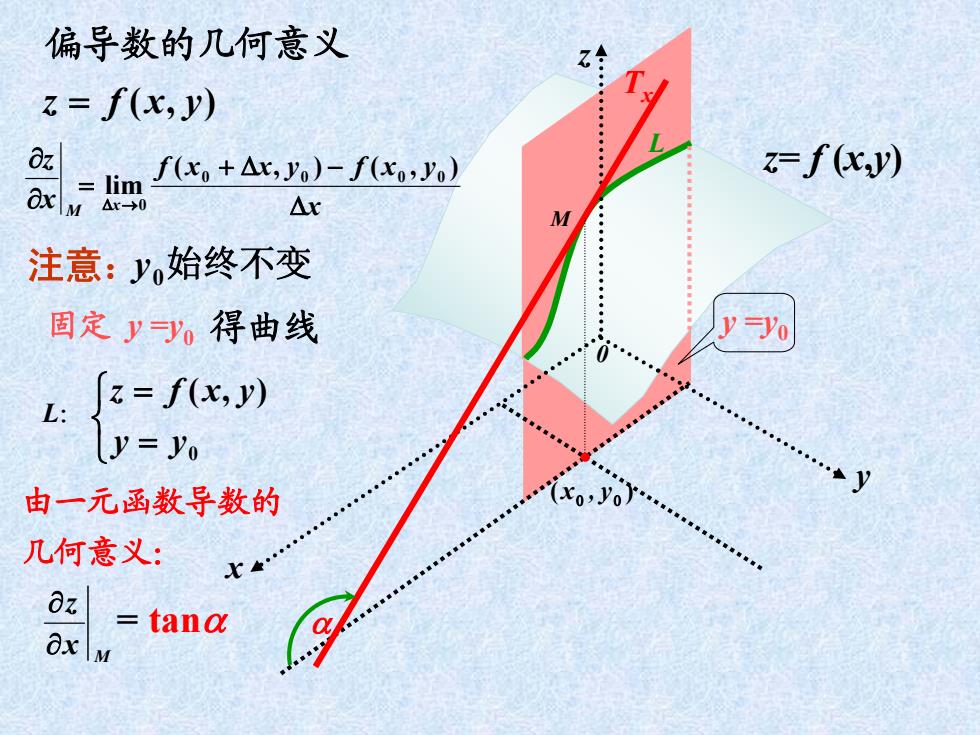
偏导数的几何意义 z=f(x,y) -im Oz f(x,+△x,y)-f(x,y) =f(K) O N △r M 注意：y始终不变 固定yy得曲线 y-Yo [z=f(x,y) y=yo 由一元函数导数的 几何意义： Oz tang xM

x z y 0  yxfz ),( M x z   x yxfyxxf x      ),(),( lim 0 0 00 0  M x z   由一元函数导数的 几何意义： z= f (x ,y )      0 ),( yy yxfz L： L 得曲线 = tan  偏导数的几何意义 y =y 0 )(  y,x M Tx 固定 y =y 0 注意： y 0始终不变

二元函数偏导数的几何意义： 0x -x5- y-Yo y=yo 在点M,处的切线MT,对x轴的斜率 副，- z=f(x,y) 在，点M处的切线MoT,对y轴的斜率

二元函数偏导数的几何意义: 0 0 ),( d d 0 0 xx yxf x x f xx yy            0 ),( yy z f yx M 0 Tx 0 0 ),( d d 0 0 yy yxf y y f xx yy       是曲线      0 ),( xx z f yx M 0 Ty 对 x 轴的斜率. 在点 M0 处的切线 对y轴的斜率. 在点 M0 处的切线 是曲线

如果一元函数在某点具有导数，则它在该点必定连 续。 思考：对于多元函数，各偏导数在某点都存在，能 否保证函数在该点连续？

如果一元函数在某点具有导数，则它在该点必定连 续。 思考：对于多元函数，各偏导数在某点都存在，能 否保证函数在该点连续？