
推论 一个n阶行列式,如果其中第i行所有 元素除外都为零,那末这行列式等于与它的 代数余子式的乘积,即D=a,A 11 L12 L13 14 例如 L21 L22 L23 D= 24 0 0 33 0 041 L42 043 044 11 12 L14 =(-1)3 33 21 u22 L24 041 L42 L44
推论 一个 阶行列式,如果其中第 行所有 元素除 外都为零,那末这行列式等于 与它的 代数余子式的乘积,即 D = aijA.ij n i aij aij 41 42 43 44 33 21 22 23 24 11 12 13 14 0 0 0 a a a a a a a a a a a a a D = ( 1) . 41 42 44 21 22 24 11 12 14 33 3 3 a a a a a a a a a a + = − 例如
二 行列式的性质 设 记 12 011 D- 21 l22 D 22 0n2 An .Qnn 行列式D'称为行列式D的转置行列式: 性质1.2.1行列式与它的转置行列式相等, 回
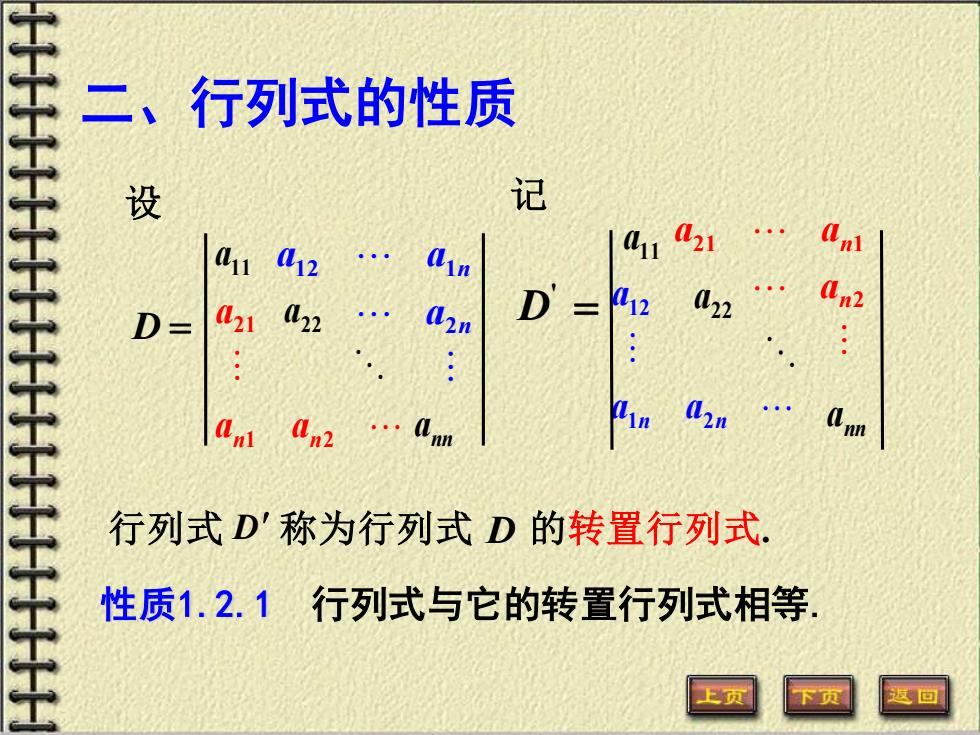
二、行列式的性质 性质1.2.1 行列式与它的转置行列式相等. 行列式 D 称为行列式 的转置行列式. D 设 nn a a a 22 11 n n a a a 2 12 1 1 2 21 n n a a a D = 2 21 1 n n a a a n n a a a 1 2 12 ' D = nn a a a 22 11 记