
曲面及其方程 一、 曲面研究的基本问题 二、 旋转曲面 三、 柱面 四、二次曲面
曲面及其方程 一、曲面研究的基本问题 二、旋转曲面 三、柱面 四、二次曲面
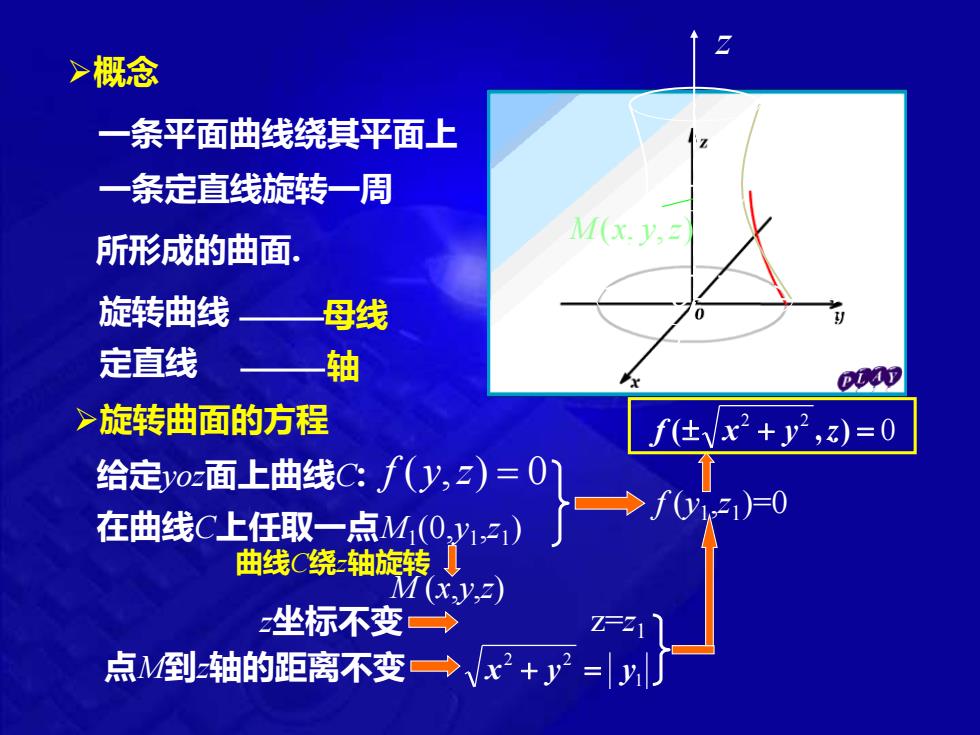
>概念 一条平面曲线绕其平面上 一条定直线旋转一周 所形成的曲面: M(x.y, 旋转曲线 母线 定直线 轴 00D >旋转曲面的方程 f(仕Vx2+y2,2)=0 给定v0面上曲线C:f(y,2)=0) 在曲线C上任取一点M(0,y1) →f0)0 曲绕轴 坐标不变一> 点M到轴的距离不变→,x2+y2=y
旋转曲线 ➢概念 母线 定直线 轴 一条平面曲线绕其平面上 所形成的曲面. 一条定直线旋转一周 ➢旋转曲面的方程 给定yoz面上曲线C: f (y,z) = 0 在曲线C上任取一点M1 (0,y1 ,z1 ) f (y1 ,z1 )=0 曲线C绕z轴旋转 M (x,y,z) z坐标不变 z=z1 点M到z轴的距离不变 1 2 2 x + y = y 0 2 2 f ( x + y ,z) = (0, , ) 1 1 1 M y z M (x, y,z) o z y x C

f仕Vx+y2,z)=0 yo面上曲线C:∫(y,z)=0绕轴旋转曲面方程 >方程的特点 〔不变 在f(y,)=0中1变为±x+y C:f(y,z)=0 类似地 当曲线Cf(y,)=0绕轴旋转,方程为: f(y,±Vx2+z2)=0
当曲线C:f (y,z)=0绕y轴旋转,方程为: C : f (y,z) = 0 o y x z ( , ) 0 2 2 f y x + z = 0 2 2 f ( x + y ,z) = yoz面上曲线C: 绕z轴旋转曲面方程 ➢方程的特点 在 f (y,z) = 0 中 z不变 y变为 2 2 x + y 类似地
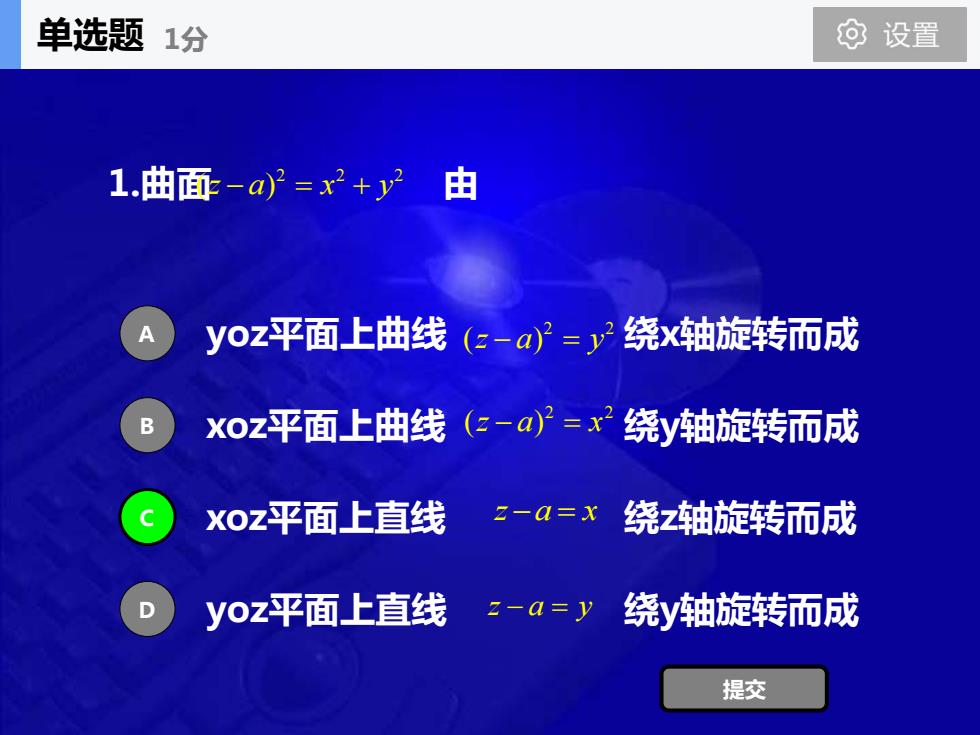
单选题1分 设置 1.曲面-a}=x2+y2由 yoz平面上曲线(e-a}=y2绕x轴旋转而成 B xoz平面上曲线(2-a)2=x绕y轴旋转而成 Xoz平面上直线2-a=x 绕z轴旋转而成 yoz平面上直线 z-a=y 绕y轴旋转而成 提交
1.曲面 由 yoz平面上曲线 绕x轴旋转而成 xoz平面上曲线 绕y轴旋转而成 xoz平面上直线 绕z轴旋转而成 yoz平面上直线 绕y轴旋转而成 A B C D 提交 2 2 2 ( ) z a x y − = + 2 2 ( ) z a y − = 2 2 ( ) z a x − = z a x − = z a y − = 单选题 1分
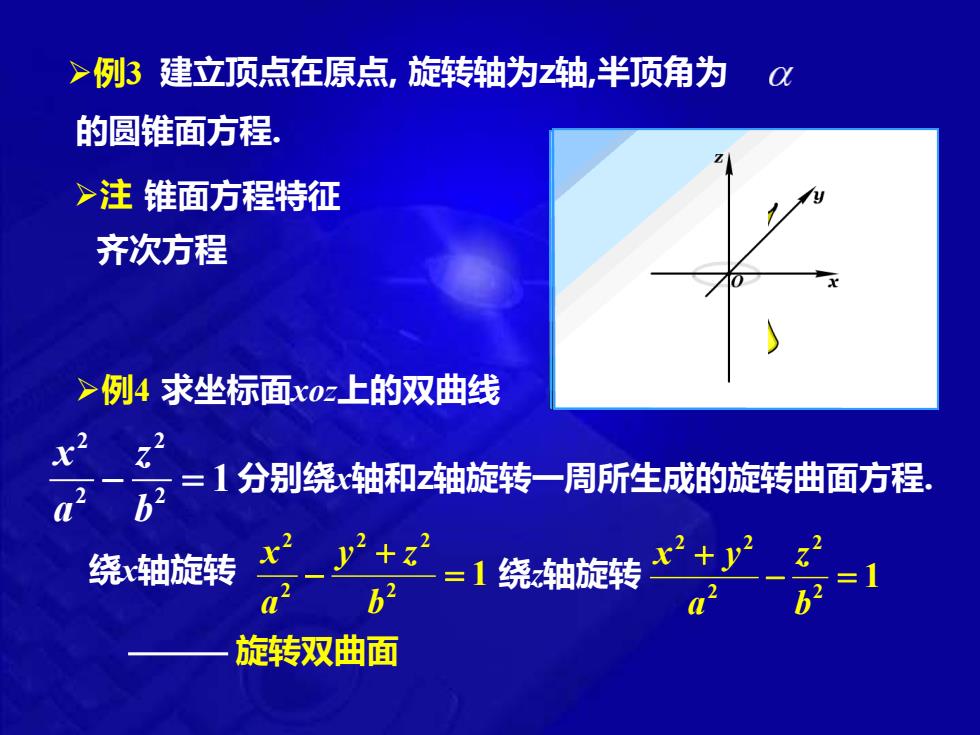
>例3 建立顶点在原点,旋转轴为z轴,半顶角为C仪 的圆锥面方程 >注锥面方程特征 齐次方程 >例4求坐标面x0z上的双曲线 x2 63 =1分别绕轴和z轴旋转一周所生成的旋转曲面方程. 绕轴旋转 x2 y2+32 =1绕轴旋转 b2 62= 旋转双曲面
建立顶点在原点, 旋转轴为z轴,半顶角为 的圆锥面方程. ➢例3 ➢例4 ➢注 锥面方程特征 齐次方程 求坐标面xoz上的双曲线 分别绕x轴和z轴旋转一周所生成的旋转曲面方程. 2 2 2 2 1 x z a b − = 绕x轴旋转 1 2 2 2 2 2 = + − b y z a x 绕z轴旋转 1 2 2 2 2 2 − = + b z a x y 旋转双曲面