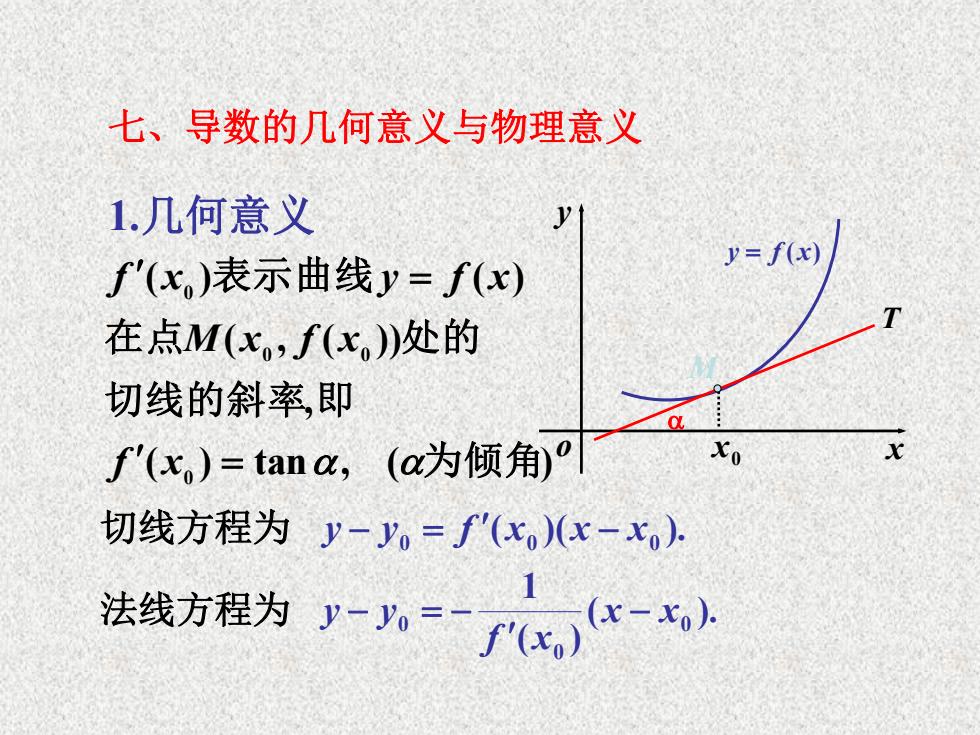
七、导数的几何意义与物理意义 1.几何意义 y y=f(x) '(x)表示曲线y=f(x) 在点M(x,f(x)处的 切线的斜率,即 '(x,)=tana,(a为倾角)° 切线方程为y-y。=f'(xx-x) 法线方程为-八=f代-x
o x y y f (x) T 0 x M 1.几何意义 ( ) tan , ( ) , ( , ( )) ( ) ( ) 0 0 0 0 为倾角 切线的斜率 即 在点 处的 表示曲线 f x M x f x f x y f x 切线方程为 法线方程为 ( )( ). 0 0 0 y y f x x x ( ). ( ) 1 0 0 0 x x f x y y 七、导数的几何意义与物理意义

例7求函数f(x)=x在点P(x,y)处的切线方程 程与法线方程 解由于 Ay=3x2+3x,△r+△x2,所以 △x f'(x)=3x 由导数的几何意义,得切线方程为 y=yo+3xp(x-xp)=3xp.x-2xg 法线方程为 1 ,3=3
由导数的几何意义, 得切线方程为 法线方程为 例7 求函数 P x y ( , ) 在点 0 0 f x x ( ) 3 处的切线方程 程与法线方程. 解 由于 , y x x x x x 0 2 2 0 3 3 所以 f x x ( ) . 2 0 0 3 y y x x x x x x ( ) . 2 2 3 0 0 0 0 0 3 3 2 y y x x x x x ( ) ( ). x x 3 0 0 0 0 2 2 0 0 1 1 3 3

2.物理意义非均匀变化量的瞬时变化率. 变速直线运动:路程对时间的导数为物体的 瞬时速度 △sds v(t)=lim -→0△tdt 交流电路:电量对时间的导数为电流强度, i(t)=lim △q=4 A-0△tdt 非均匀的物体:质量对长度面积,体积)的导 数为物体的线面,体)密度
2.物理意义 非均匀变化量的瞬时变化率. 变速直线运动:路程对时间的导数为物体的 瞬时速度. ( ) lim . 0 dt ds t s v t t 交流电路:电量对时间的导数为电流强度. ( ) lim . 0 dt dq t q i t t 非均匀的物体:质量对长度(面积,体积)的导 数为物体的线(面,体)密度

八、可导与连续的关系 定理凡可导函数都是连续函数: 证设函数f(x)在点x,可导,且im △y=f(x) △x→0△X 则 -)+a其中a→0(→0)从而 △y=f'(xo)△x+ax 故imAy=m/'(x)△r+a△r=0.函数f(x)在点x,连续 注1:△y=f'(x)△x+a△x称为有限增量公式. 注2:该定理的逆命题不真即连续函数不一定可导
定理 凡可导函数都是连续函数. y f (x0 )x x 八、可导与连续的关系 证 ( ) , 设函数 f x 在点x0可导 lim ( ) 0 0 f x x y x 且 ( ) x0 f x y 则 其中 0 (x 0) 从而 lim lim[ ( ) ] 0 0 0 0 y f x x x x x ( ) . 故 函数 f x 在点x0连续 注1: y f (x0 )x x 称为有限增量公式. 注2: 该定理的逆命题不真.即连续函数不一定可导

连续函数不存在导数举例 1.函数f(x)连续,若f'(x)≠f(x)则称点x。 为函数f(x)的角点,函数在角点不可导. 例如, -f,xso , x>0 在x=0处不可导,x=0为fx)的角点
连续函数不存在导数举例 ( ) , . 1. ( ) , ( ) ( ) 0 0 0 为函数 的角点 函数在角点不可导 函 数 连 续 若 则称点 f x f x f x f x x x y 2 y x 0 例如, y x , , 0 , 0 ( ) 2 x x x x f x 在 x 0处不可导, x 0为 f (x)的角点