
第十章定积分的应用 §1平面图形的面积 §2由平行截面面积求体积 §3平面曲线的弧长 §4旋转曲面的面积 §5定积分在物理中的应用
§3 平面曲线的弧长 §4 旋转曲面的面积 §1平面图形的面积 §5 定积分在物理中的应用 §2 由平行截面面积求体积 第十章 定 积 分的应用

§10.1平面图形的面积 一、直角坐标系情形 二、参数方程 三、极坐标情形 四、小结
§10.1平面图形的面积 一、直角坐标系情形 二、参数方程 三、极坐标情形 四、小结
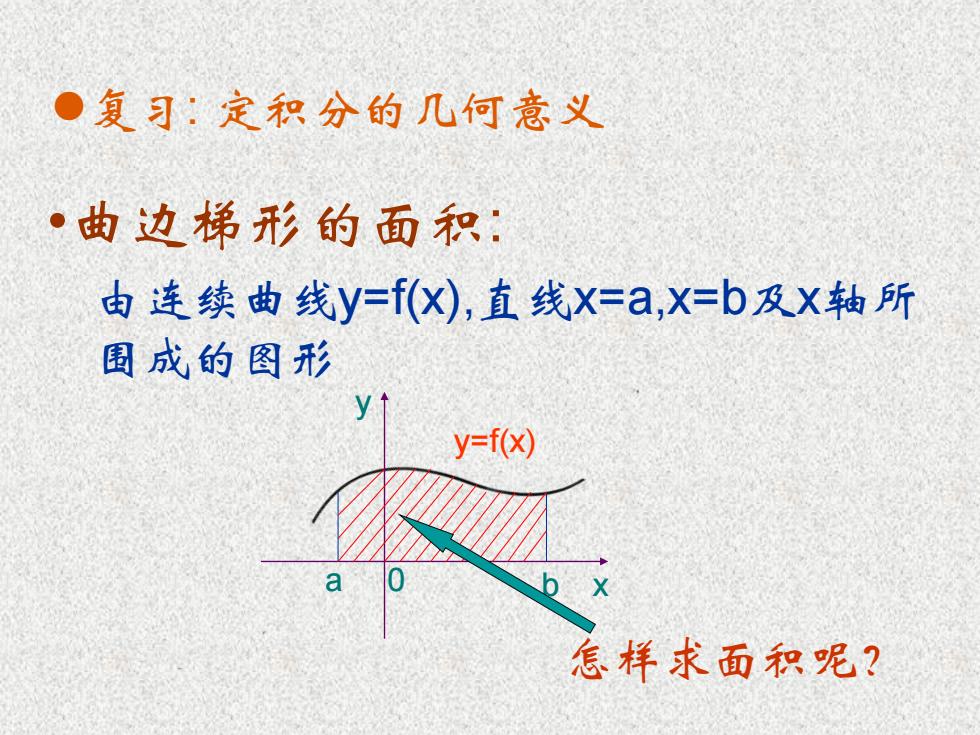
●复习:定积分的几何意义 ·曲边梯形的面积: 由连续曲线y=f((X),直线X=a,X=b及X轴所 围成的图形 y=f(x) 怎样求面积呢?
复习: 定积分的几何意义 •曲边梯形的面积: 由连续曲线y=f(x),直线x=a,x=b及x轴所 围成的图形 y=f(x) a 0 b x y 怎样求面积呢?

-Af(x)<0 A表示以y=f)为曲边的曲边梯形面积 yt y=f(x)>0 y↑ y=f(x)<0
f x dx b a 1. ( ) A -A f (x) 0 f (x) 0 A表示以y=f(X)为曲边的曲边梯形面积 a b a b y=f(x)>0 y=f(x)<0 x x y y 0 0 A A
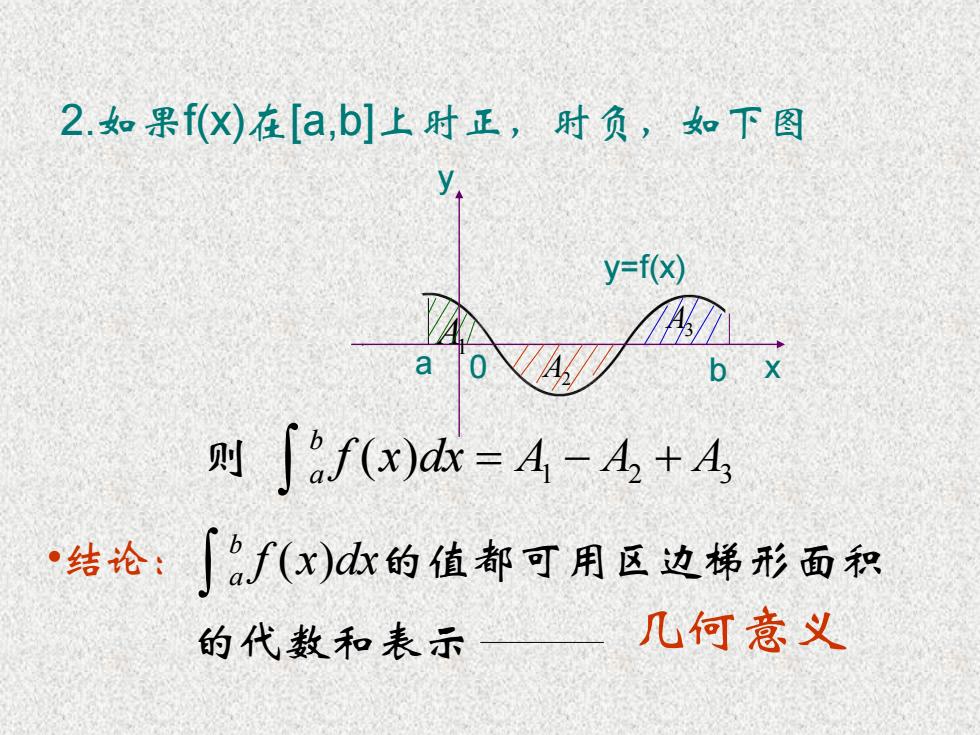
2.如果f()在[a,b]上时正,时负,如下图 y=f(x) b x 则∫f(x)d=A-A+A 结论:∫f(x)的值都可用区边梯形面积 的代数和表示 几何意义
1 2 3 f (x)dx A A A b a 则 2.如果f(x)在[a,b]上时正,时负,如下图 •结论: 的代数和表示 b a f (x)dx的值都可用区边梯形面积 几何意义 a b x y y=f(x) A2 A1 A3 0