
第六章微分中值定理及应用 ·6.1拉格郎日定理和函数的单调性 ·6.2柯西中值定理和不定式极限 ·6.3泰勒公式 ·6.4函数的极值与最大最小值 ·6.5函数的凸性和拐点 ·6.6函数图像的讨论
• 6.1 拉格郎日定理和函数的单调性 • 6.2 柯西中值定理和不定式极限 • 6.3 泰勒公式 • 6.4 函数的极值与最大最小值 • 6.5 函数的凸性和拐点 • 6.6 函数图像的讨论

6.1拉格朗日定理和☒数的单调性 ·一、罗尔定理 ·二、拉格郎日定理 ·三、单调函数
• 一、罗尔定理 • 二、拉格郎日定理 • 三、单调函数

微分中值定理的核心是拉格朗日(Lagrange) 中值定理,费马定理是它的预备定理,罗尔定理 是它的特例,柯西定理是它的推广。 一、预备定理 费马Fermat)定理 若函数fx)在(a,b)内一点x取得极值,且fx)在x可微,则 f'(x)=0. 费马(Fermat,1601-1665),法国人, 与笛卡尔共同创立解析几何。因提出费马 大、小定理而著名
微分中值定理的核心是拉格朗日(Lagrange) 中值定理,费马定理是它的预备定理,罗尔定理 是它的特例,柯西定理是它的推广。 一、预备定理——费马(Fermat)定理 费马(Fermat,1601-1665),法国人, 与笛卡尔共同创立解析几何。因提出费马 大、小定理而著名。 ( ) 0. 0 f x = 若函数f(x)在(a,b)内一点x0取得极值,且f(x)在x0可微,则
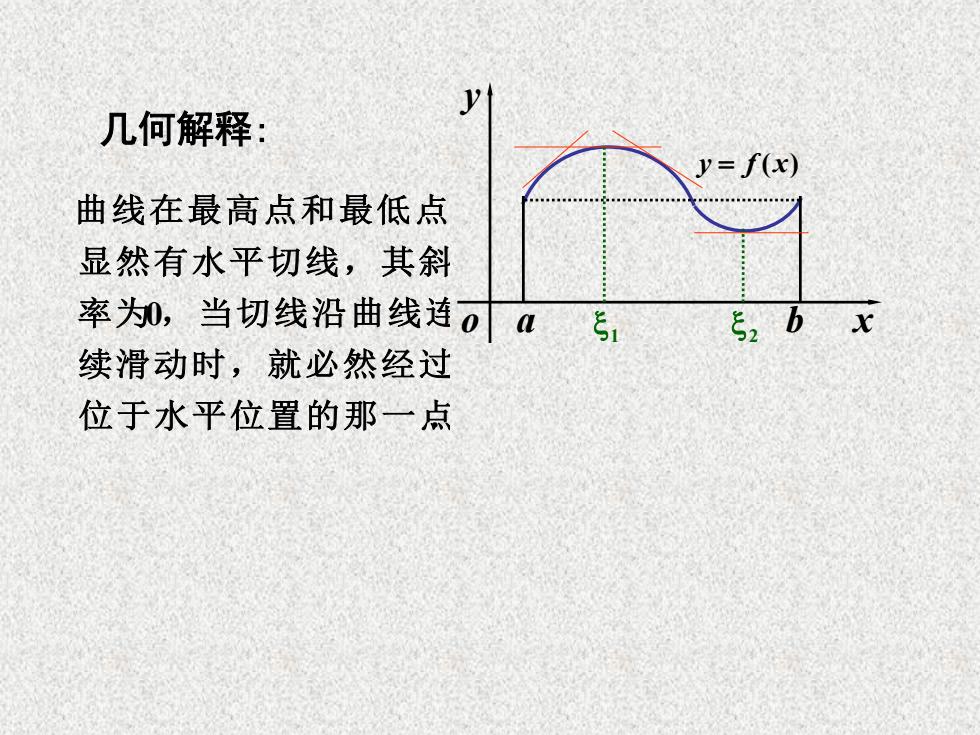
y 几何解释: y=f(x) 曲线在最高点和最低点 显然有水平切线,其斜 率为0,当切线沿曲线连oa E2b x 续滑动时,就必然经过 位于水平位置的那一点
x y o y = f (x) a b 1 2 几何解释: . 0 位于水平位置的那一点 续滑动时,就必然经过 率 为 ,当切线沿曲线连 显然有水平切线,其斜 曲线在最高点和最低点

证明:只就fx)在x取极大值的情形给出证明。 由于fx)在x取极大值,所以存在δ>0,当x∈Uc,δ)时,有 fx)sfx),又fx)在x可导,所以f'(x)=f(x)=f'(x) 而 fx)=1mf)-fs0, x-→x0+ x-xo f(xo)=lim f(x)-fx≥0, x-xo-X-o 所以f'(x)=0:
证明: 只就f(x)在x0取极大值的情形给出证明. 由于f(x)在x0取极大值,所以存在>0,当xU(x0 , )时,有 f(x) f(x0 ),又f(x)在x0可导,所以 而 ( ) ( ) ( ) lim , x x f x f x f x x x = 0 0 0 0 0 ( ) ( ) ( ) lim , x x f x f x f x x x = 0 0 0 0 0 所以 f x f x f x ( ) ( ) ( ). 0 0 0 = = 所以 f x ( ) . 0 = 0