
2.设函数f(x)在点x,连续,但 四是=四+0-- △x 称函数f(x)在点x有无穷导数.(不可导) 例如, f(x)=x-1, x 在x=1处不可导
3 y x 1 x y 0 1 例如, ( ) 1, 3 f x x 在 x 1处不可导. ( ) .( ) 称函数 f x 在点 x0有无穷导数 不可导 2. ( ) , 设函数 f x 在点 x0连续 但 , ( ) ( ) lim lim 0 0 0 0 x f x x f x x y x x
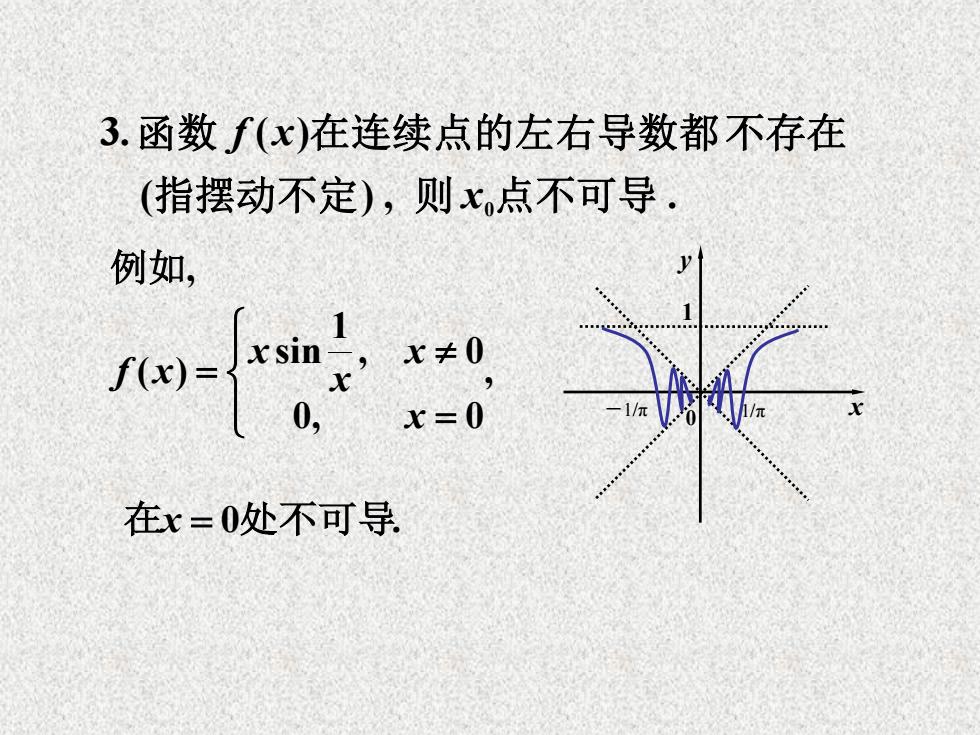
3.函数f(x)在连续点的左右导数都不存在 (指摆动不定),则x点不可导. 例如, 小 x≠0 x=0 在x=0处不可导
, 0, 0 , 0 1 sin ( ) x x x x f x 例如, 在x 0处不可导. 0 1 -1/π 1/π x y ( ) , . 指摆动不定 则 x0点不可导 3.函数 f (x)在连续点的左右导数都不存在

4.若f'(x,)=o∞,且在点x的两个单侧导数 符号相反,则称点x为函数f(x)的尖点 (不可导点). y=f(x) Xo
x y o x y 0 o x y f (x) y f (x) (不可导点) . , ( ) 符号相反 则称点 x0为函数 f x 的尖点 4. ( ) , 若f x0 且在点 x0的两个单侧导数

例8讨论函数 x=0 在x=0处的连续性与可微性
例8 讨论函数 1 0 0 0 sin , ( ) , k x x f x x x 在x=0处的连续性与可微性

解因sin!是有界函数.所以mrin上0k>0 >0 从而k20时,f0)=imf(x)=0即x在x-0连续. 又在x=0处,有 △y (0+Ax)sin 1 ()si △x △c=(△x)-sin △x △x △x 所以>1时,fx)在x=0可导,且f'(0)=0
1 1 1 0 0 0 1 ( ) sin ( ) sin ( ) sin k k k x x y x x x x x x x 0 ( ) lim ( ) 0 0 x f f x 解 因 1 sin x 0 1 lim sin ( ) 0 0 k x x k x 是有界函数,所以 从而k>0时, 即f(x)在x=0连续. 又在x=0处,有 所以k>1时, f(x)在x=0可导,且 f ( ) . 0 0