
§1含参量正常积分 对多元函数其中的一个自变量进行积 分形成的函数称为含参量积分,它可用来 构造新的非初等函数.含参量积分包含正 常积分和非正常积分两种形式: 前顶 后页 返回
前页 后页 返回 §1 含参量正常积分 对多元函数其中的一个自变量进行积 分形成的函数称为含参量积分, 它可用来 构造新的非初等函数. 含参量积分包含正 常积分和非正常积分两种形式

一、含参量正常积分的定义 设f(x,y)是定义在矩形区域R=[,b]×[c,W上的 二元函数.当x取[a,b上的定值时,函数f(x,y)是 定义在[c,上以y为自变量的一元函数.倘若这时 f(x,y)在[c,上可积,则其积分值 Ix)=∫fxy,x∈a,1 (I) 是定义在[a,b]上的函数 一般地,设f(x,y)为定义在区域
前页 后页 返回 一、含参量正常积分的定义 设 f x y ( , ) 是定义在矩形区域 R a b c d [ , ] [ , ] 上的 定义在 [ , ] c d 上以 y 为自变量的一元函数. 倘若这时 f x y ( , ) 在 [ , ] c d 上可积, 则其积分值 ( ) ( , )d , [ , ] (1) d c I x f x y y x a b 是定义在 [ , ] a b 上的函数. 一般地, 设 f x y ( , ) 为定义在区域 二元函数.当 x取 [ , ] a b 上的定值时,函数 f x y ( , ) 是
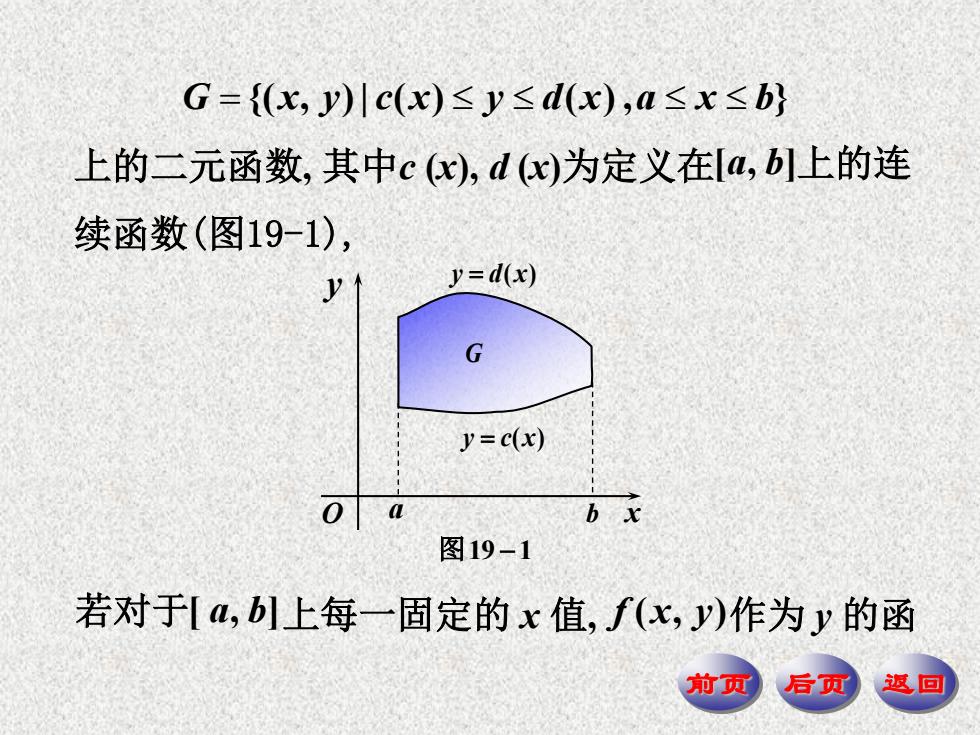
G={(x,y)川c(x)≤y≤d(x),a≤x≤b} 上的二元函数,其中c(x),dx)为定义在a,b]上的连 续函数(图19-1), ↑ y=d(x) G y=c(x) bx 图19-1 若对于[a,]上每一固定的x值,∫(x,)作为y的函 前页 后页 返回
前页 后页 返回 G x y c x y d x a x b {( , ) | ( ) ( ) , } 上的二元函数, 其中c (x), d (x)为定义在 [ , ] a b 上的连 续函数(图19-1), 图19 1 O y a b x G y c x ( ) y d x ( ) 若对于 [ , ] a b 上每一固定的 x 值, f x y ( , ) 作为 y 的函

数在闭区间[c(x),d(x)]上可积,则其积分值 F()( (2) 是定义在[a,b]上的函数 用积分形式(1)和(2)所定义的这函数I(x)与F(x) 通称为定义在[4,]上的含参量x的(正常)积分, 或简称为含参量积分, 前顶 返回
前页 后页 返回 数在闭区间 [ ( ), ( ) ] c x d x 上可积, 则其积分值 ( ) ( ) ( ) ( , )d , [ , ] (2) d x c x F x f x y y x a b 是定义在 [ , ] a b 上的函数. 用积分形式 (1) 和 (2) 所定义的这函数 I x( ) 与 F x( ) 通称为定义在 [ , ] a b 上的含参量 x 的(正常)积分, 或简称为含参量积分

二、含参量正常积分的连续性 定理19.1(I(x)的连续性)若二元函数f(x,y)在矩 形区域R=[a,b]×[c,d上连续,则函数 Ix)=∫fx,y 在[a,b]上连续 证设x∈[a,b,对充分小的△x,有x+△x∈[a,b(若 x为区间的端点,则仅考虑△>0或△x<0),于是 前页 后页 返回
前页 后页 返回 二、含参量正常积分的连续性 定理19.1 ( I x( )的连续性 ) 若二元函数 f x y ( , ) 在矩 形区域 R a b c d [ , ] [ , ] 上连续, 则函数 ( ) ( , )d d c I x f x y y 在[ a , b]上连续. 证 设 x a b [ , ], 对充分小的 x x x a b , [ , ] 有 (若 x 为区间的端点, 则仅考虑 x x 0 0 或 ), 于是