
定理函数fx)在点x,处可导台左导数和右导数都存在 且相等即f(x)与f(x)存在且f(x)=f'(x。), 此时f'(x)=f(x)=(x)
定理 函数f(x)在点x0处可导左导数和右导数都存在 ( ) x0 f ( ) x0 f 且相等 .即 与 存在且 f x f x ( ) ( ). 0 0 此时 f x f x f x ( ) ( ) ( ). 0 0 0

五、导函数 若函数在区间上每个点处可导(对区间的端点,只考 虑单侧导数),则称f为L上的可导函数这时对每个x∈都有 一个导数f'(x)(或单侧导数)与之对应,从而就定义了一个 I上的新函数,称为f在L上的导函数,也称为导数.记作 f子y或山即 f'w=lim+Ao)-f四,xeL △x→0 △x
若函数f在区间I上每个点处可导 (对区间的端点,只考 五、 导函数 虑单侧导数),则称f为I上的可导函数.这时对每个xI都有 一个导数 f x ( ) (或单侧导数)与之对应,从而就定义了一个 I上的新函数,称为f在I上的导函数,也称为导数.记作 f y , 或 , dy dx 即 ( ) ( ) ( ) lim , . x f x x f x f x x I x 0

注1如果f(x)在开区间(a,b)内可导,且f+(a)及f(b) 都存在,就说fx)在闭区间[a,b上可导. 注2分段函数 fe)=oxx≥ Ψ(x),x<x 在分点x处的可导性只能用单侧导数进行讨论
注1 如果f (x)在开区间(a,b)内可导,且 f (a) 及f (b) 都存在,就说f(x)在闭区间[a,b]上可导. 注2 ( ), ( ) ( ), x x x f x x x x 0 0 分段函数 在分点x0处的可导性只能用单侧导数进行讨论
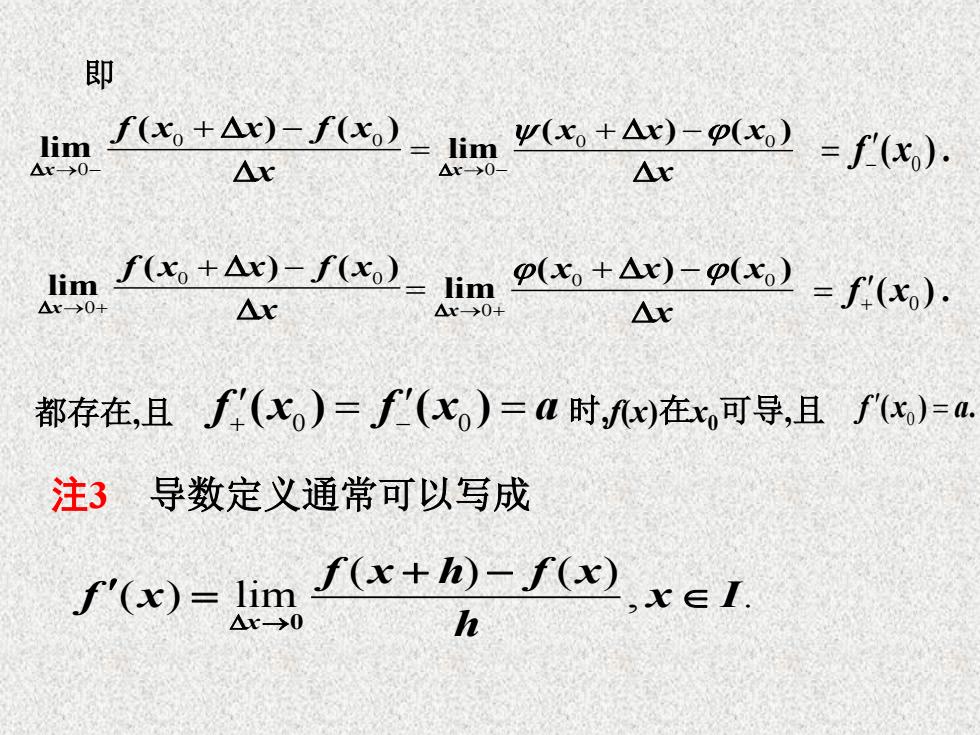
即 lim f(x。+△x)-f(x) -1imy(x+Ae)-p(x) △x>0 △x △x>0 △x =f(x) imfx+Ae)-fx)-1img+Ae)-p)=fx,). △x→0+ △x x30 △x 都存在,且f(x)=f'()=a时,fx)在x可导,且fx)=a 注3 导数定义通常可以写成 f(x)=lim f-f().x1. △x-→0 h
0 0 0 ( ) ( ) lim x f x x f x x 0 0 0 ( ) ( ) lim x x x x x 0 f x( ) . 即 0 f x( ) . 0 0 0 ( ) ( ) lim x f x x f x x 0 0 0 ( ) ( ) lim x x x x x 都存在,且 0 0 f x f x a ( ) ( ) 时,f(x)在x0可导,且 0 f x a ( ) . 注3 导数定义通常可以写成 ( ) ( ) ( ) lim , . x f x h f x f x x I h 0

六、由定义求导数 步骤:(①)求增量△y=f(x+△x)-f(x): (2)算比值 △y=f(x+A)-f(x) △x △x (3)求极限 y'=lim △y Ar-→0△x 例1求函数f(x)=C(C为常数)的导数 解fx=mfx+c)-f田-1mC-C h-→0 x h-0△x -0. 即 (C)'=0
步骤: (1)求增量 y f (x x) f (x);; ( ) ( ) (2) x f x x f x x y 算比值 (3) lim . 0 x y y x 求极限 例1 求函数 f (x) C(C为常数)的导数. 解 ( ) ( ) ( ) limh f x x f x f x x 0 lim h C C x 0 0. 即 (C) 0. 六、由定义求导数