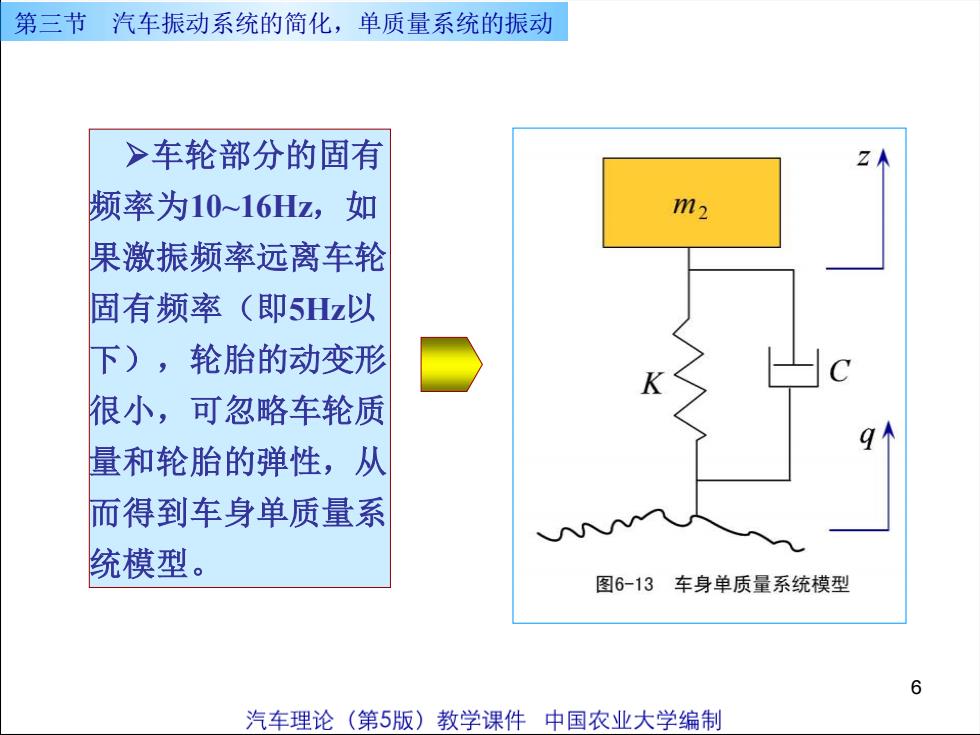
第三节汽车振动系统的简化,单质量系统的振动>车轮部分的固有1频率为10~16Hz,如m2果激振频率远离车轮固有频率(即5Hz以下),轮胎的动变形很小,可忽略车轮质量和轮胎的弹性,从而得到车身单质量系SS统模型。图6-13车身单质量系统模型6汽车理论(第5版)教学课件中国农业大学编制
6 ➢车轮部分的固有 频率为10~16Hz,如 果激振频率远离车轮 固有频率(即5Hz以 下),轮胎的动变形 很小,可忽略车轮质 量和轮胎的弹性,从 而得到车身单质量系 统模型。 第三节 汽车振动系统的简化,单质量系统的振动
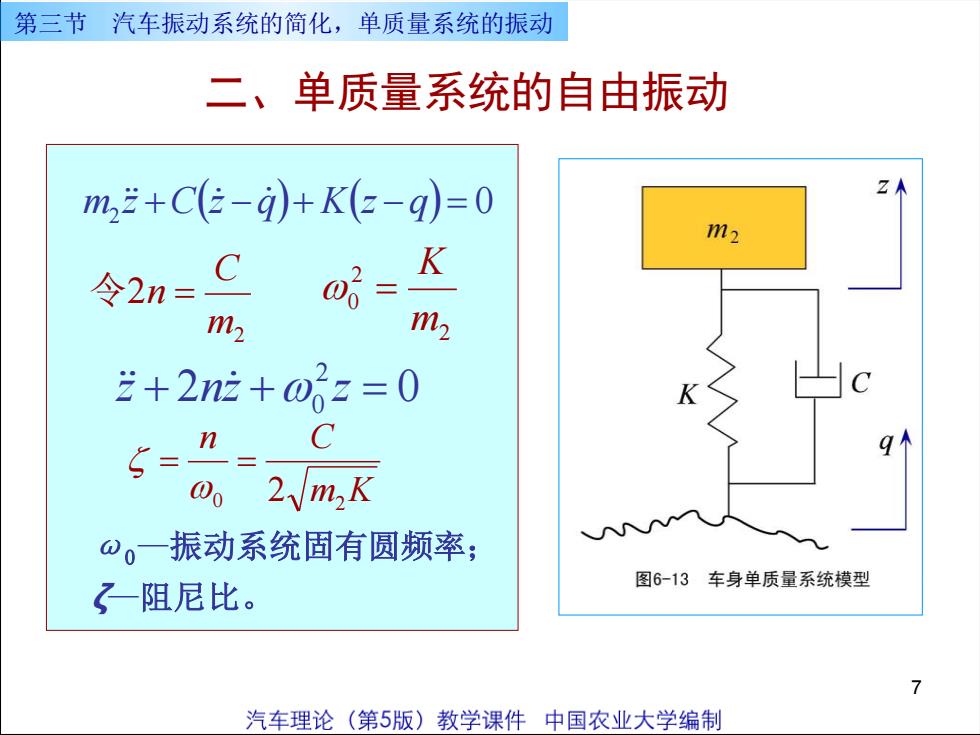
第三节汽车振动系统的简化,单质量系统的振动二、单质量系统的自由振动Zm,z+C(z-9)+K(z-q)= 0m2KC0=令2n=m2m2艺+2nz+0z=0nqa2/m,K0Sの一振动系统固有圆频率;图6-13车身单质量系统模型一阻尼比。7汽车理论(第5版)教学课件中国农业大学编制
7 二、单质量系统的自由振动 m2 z +C(z −q )+ K(z −q) = 0 2 2 m C 令 n = 2 2 0 m K = 2 0 2 z + nz +0 z = m K n C 0 2 2 = = ω0—振动系统固有圆频率; ζ—阻尼比。 第三节 汽车振动系统的简化,单质量系统的振动
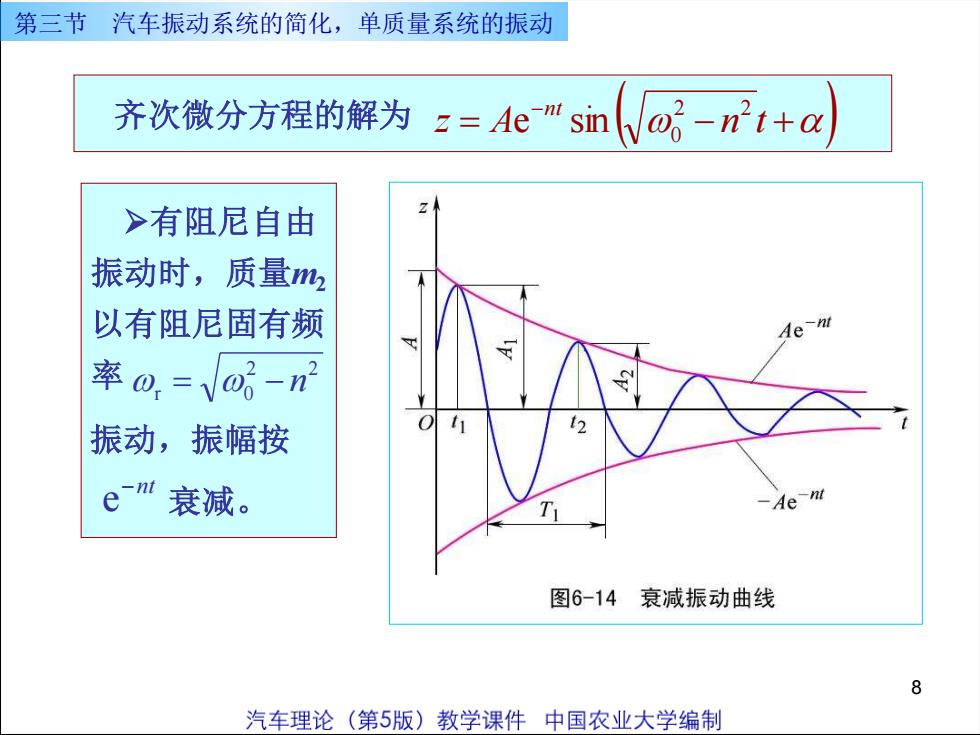
第三节汽车振动系统的简化,单质量系统的振动齐次微分方程的解为 z= Ae-" sin(V/-n’t+α>有阻尼自由振动时,质量m以有阻尼固有频Ae-nt率,=-n2振动,振幅按e-n 衰减。Ae-nt图6-14衰减振动曲线8汽车理论(第5版)教学课件中国农业大学编制
8 齐次微分方程的解为 = ( − +) − z A n t nt 2 2 0 e sin 第三节 汽车振动系统的简化,单质量系统的振动 ➢有阻尼自由 振动时,质量m2 以有阻尼固有频 率 2 2 r 0 = − n 振动,振幅按 e −nt 衰减

第三节汽车振动系统的简化,单质量系统的振动阻尼比对衰减振动的影响1)与有阻尼固有频率の,有关0, = -n? =/1-2>增大,の下降。当-时,运动失去振荡特征>汽车悬架系统阻尼比大约为0.25,,比0只下降了3%左右,0~0KK0o82元m2m9汽车理论(第5版)教学课件中国农业大学编制
9 ➢ζ增大,ωr下降。当ζ=1时,运动失去振荡特征。 ➢汽车悬架系统阻尼比ζ大约为0.25,ωr比ω0只下降了 3%左右, 。 1)与有阻尼固有频率ωr有关 2 2 r 0 = − n 2 0 = 1− r 0 2 0 m K = 2 0 0 2π 1 2π m K f = = 第三节 汽车振动系统的简化,单质量系统的振动 阻尼比ζ对衰减振动的影响

第三节汽车振动系统的简化,单质量系统的振动阻尼比对衰减振动的影响2)决定振幅的衰减程度两个相邻的振幅A,与A,之比称为减振系数d2元2Ae-ntid=A=eVi-sAe-n(i+T) =enlA阻尼比越大,振幅衰减得越快2元Ind1+4元2/ln2d/1-2由实测的衰减振动曲线得到d,即可确定系统的阻尼比。10汽车理论(第5版)教学课件中国农业大学编制
10 2)决定振幅的衰减程度 2 1 A A d = ( ) 1 1 1 e e n t T nt A A − + − = 1 e nT = 2 1 2π e − = 2 1 2π ln − d = d 2 2 1 4π ln 1 + / = 阻尼比ζ对衰减振动的影响 两个相邻的振幅A1与A2之比称为减振系数d 由实测的衰减振动曲线得到d,即可确定系统的阻尼比ζ。 阻尼比越大,振幅衰减得越快 第三节 汽车振动系统的简化,单质量系统的振动