《汽车理论》课程教学课件（PPT讲稿）第六章 汽车的平顺性 6.4 车身与车轮双质量系统的振动

第六章汽车的平顺性第四节车身与车轮双质量系统的振动Z2m2K<ZKt4汽车理论（第5版）教学课件中国农业大学编制

1 第四节 车身与车轮双质量系统 的振动 第六章 汽车的平顺性

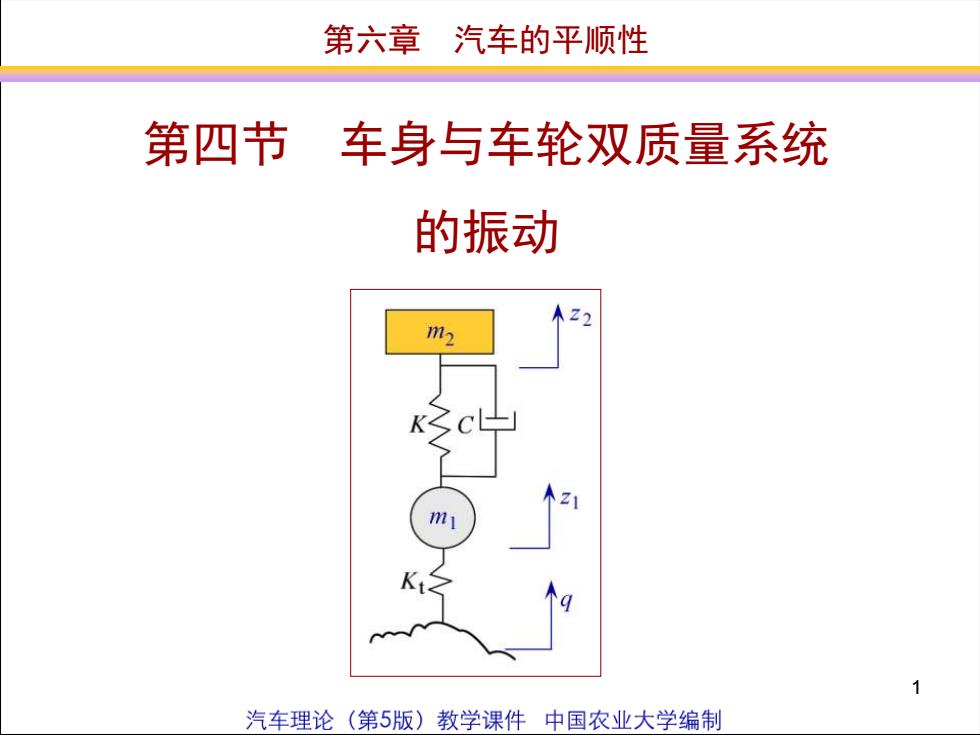
第四节车身与车轮双质量系统的振动、运动方程和振型分析m,2, +C(, -2)+ K(z, -z)=0AZ2m2m=+C(-z2)+K(1-z2)+K,(=1-9)=0无阻尼自由振动时m,+K(,-z)=0Cm=, +K( -z2)+K,z) =0zim如果m不动（zi=0）m= +Kz2 =00= /K /m2KtTq如果m2不动（z2=0）m+(K+K)zi = 0图6-21车身与车轮两个0, = /(K +K)/ m自由度振动系统>の与の,是双质量系统只有单独一个质量振动时的部分频率（偏频）2汽车理论（第5版）教学课件中国农业大学编制

2 一、运动方程和振型分析 ( ) ( ) ( ) ( ) ( )    + − + − + − = + − + − = 0 0 1 1 1 2 1 2 t 1 2 2 2 1 2 1 m z C z z K z z K z q m z C z z K z z       无阻尼自由振动时 ( ) ( )    + − + = + − = 0 0 1 1 1 2 t 1 2 2 2 1 m z K z z K z m z K z z   如果m1不动（z1=0） m2  z  2 + Kz2 = 0 0 2  = K / m 如果m2不动（z2=0） m1  z  1 + (K + Kt )z1 = 0 ( ) t K Kt m1  = + / ➢ω0与ωt是双质量系统只有单独一个质量振动时的部分频率（偏频）。 第四节 车身与车轮双质量系统的振动

第四节车身与车轮双质量系统的振动>无阻尼自由振动时，设两个质量以相同的圆频率の和相角β做简谐振动，振幅为z10、20Zi = 21oe ;(o+0)Z2 = 220e ;(ot+0)zi = -2100'ej(o+0)z2 = -2200'e (ou+0)代入 m2z2 +K(22 -2)=0得mz) + K( - z2)+ K,z = 0KKr0=K/mZ10 =000+20将m2m20=(K+K)/mKK+K210=0Z100220代入左式后可得mim3汽车理论（第5版）教学课件中国农业大学编制

3 ➢无阻尼自由振动时，设两个质量以相同的圆频率ω 和相角 做简谐振动，振幅为z10、z  20 。 ( + ) = ωt z j 1 10 z e ( + ) = t z j 2 20 z e (  )  + = − t z 2 j 1 10  z  e (  )  + = − ωt z 2 j 2 20  z  e 10 0 2 20 2 2 − 20 + − z = m K z m K z  0 10 1 t 20 1 2 10 = + − − + z m K K z m K z  2 2 0  = K / m ( )t 1 2 t  = K + K / m 将 代入左式后可得 代入 ( ) ( )    + − + = + − = 0 0 1 1 1 2 t 1 2 2 2 1 m z K z z K z m z K z z   得 第四节 车身与车轮双质量系统的振动

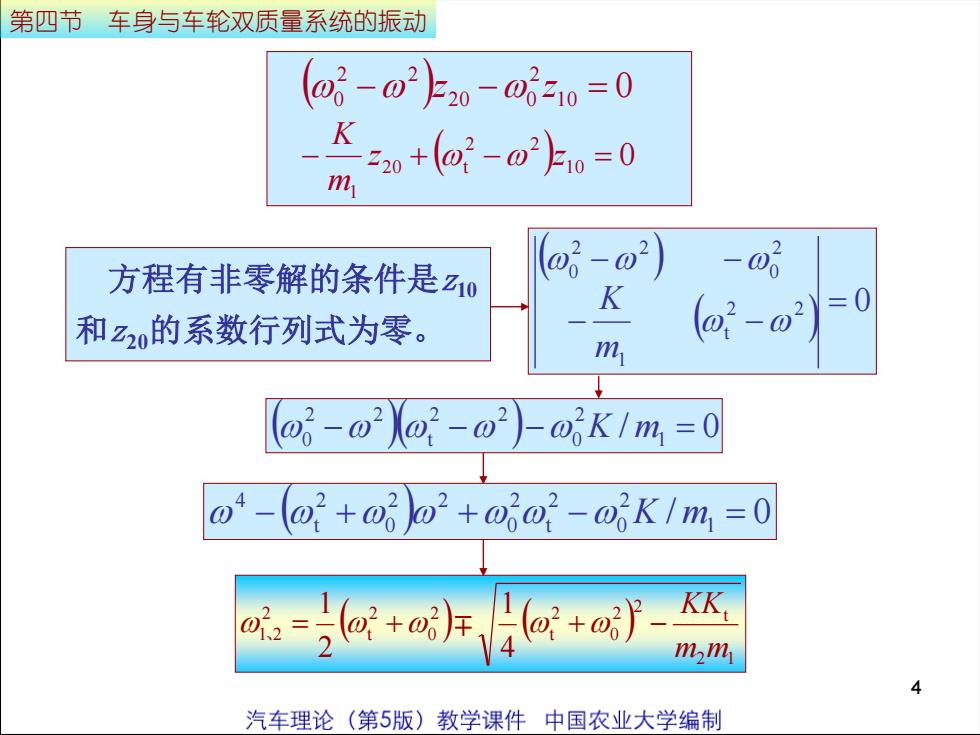
第四节车身与车轮双质量系统的振动(0 - 0)20 -=10 = 0-=20 +(0~ -0°)1 =0m(o? -?)-0方程有非零解的条件是Z10K(o? -02)=0和z20的系数行列式为零。m( -Xo? -02)-0K / m = 004-(o +0)0? +00-0K / m =0%2=( +%)/(2 +%) -m,m,汽车理论（第5版）教学课件中国农业大学编制

4 方程有非零解的条件是z10 和z20的系数行列式为零。 ( ) ( ) 2 2 0 t 1 2 0 2 2 0 = − − − −      m K ( )( ) / 1 0 2 0 2 2 t 2 2 0 −  − − K m = ( ) ( ) 2 1 t 2 2 0 2 t 2 0 2 t 2 1 2 4 1 2 1 m m KK  、 =  +   + − ( ) 10 0 2 20 0 2 2 0 − z − z = ( ) 10 0 2 2 20 t 1 − z + − z = m K   第四节 车身与车轮双质量系统的振动 ( ) / 1 0 2 0 2 t 2 0 2 2 0 2 t 4  −  +  +  − K m =

第四节车身与车轮双质量系统的振动例设某一汽车の=2元rad/s，质量比u=m,/m=10,刚度比=K/K=9，求和,?由K,=9K,m =m2 /10得02 =(K +K,)/ m = 10000f =1000KK,= 900m,m求得Q =0.950o0, = 10.0105汽车理论（第5版）教学课件中国农业大学编制

5 设某一汽车 2πrad/s 0 = 10 μ = m2 /m1 = 9 γ = Kt /K = ，求ω1和ω2? t 由K K = 9 ，m1 = m2 /10得 ( )t 1 2 t  = K + K / m 2 =1000 t =100 4 0 2 1 t = 90 m m KK 1 95 0 求得 = 0.  2 01 0  =10.  ，质量比 ， 刚度比 例 第四节 车身与车轮双质量系统的振动