
第6章教学方案-拉伸、压缩与剪切轴向拉伸、压缩的概念和内力分析轴向拉伸和压缩时横截面上的应力基本内中材料拉伸和压缩时的力学性能失效、安全因数和强度计算轴向拉伸和压缩时的变形容拉伸和压缩的简单静不定问题剪切与挤压的实用计算掌握用截面法计算拉、压杆的内力,画内力图。、掌握拉、压杆的截面上应力分析。3、理解材料在拉压时的变形、应力、破坏等的特性。教学目4、熟练掌握拉、压杆的的强度计算。、熟练掌握拉、压杆的的变形计算及胡克定律的了解拉、压杆的简单静不定问题。、掌握剪切和挤压的实用计算,重点拉、压杆的强度计算;拉、压杆的的变形计算。难点
第 6 章 教学方案 ——拉伸、压缩与剪切 基 本 内 容 轴向拉伸、压缩的概念和内力分析 轴向拉伸和压缩时横截面上的应力 材料拉伸和压缩时的力学性能 失效、安全因数和强度计算 轴向拉伸和压缩时的变形 拉伸和压缩的简单静不定问题 剪切与挤压的实用计算 教 学 目 的 1、掌握用截面法计算拉、压杆的内力,画内力图。 2、掌握拉、压杆的截面上应力分析。 3、理解材料在拉压时的变形、应力、破坏等的特性。 4、熟练掌握拉、压杆的的强度计算。 5、熟练掌握拉、压杆的的变形计算及胡克定律。 6、了解拉、压杆的简单静不定问题。 7、掌握剪切和挤压的实用计算。 重 点 、 难 点 拉、压杆的强度计算;拉、压杆的的变形计算
第6章拉伸、压缩与剪切6.1轴向拉伸、压缩的概念和内力分析6.1.1轴向拉伸和压缩的工程实例主生产实践中经常遇到承受拉伸或压缩的杆件。例如,图6.1(a)所示的简单吊物装置的两根杆件,图6.2(b)所示的螺杆等。合(b)a)图6.16.1.2轴向拉伸和压缩的特点轴向拉伸和压缩杆件的计算简图如图6.2所示,从图中可看出当一个杆件发生轴向拉伸和压缩变形时具有如下特点:H图 6.2受力特点:外力作用线沿杆轴线方向且与轴线重合·变形特点:杆件变形是沿轴线的方向伸长或缩短,横向的缩短或伸长6.1.3轴向拉伸和压缩时横截面上的内力●截面法求内力:图6.3(a)所示为一受轴向拉伸的直杆,在横截面m-m处将杆截为两段,取(a)左段为研究对象,如图6.3(b)所示。由左段的平衡条件可知,该截N面上分布内力的合力必为一个与(b)杆件轴线重合的轴向力FN,且有出FN=F,F称为轴力。若取右(e)图 6.3
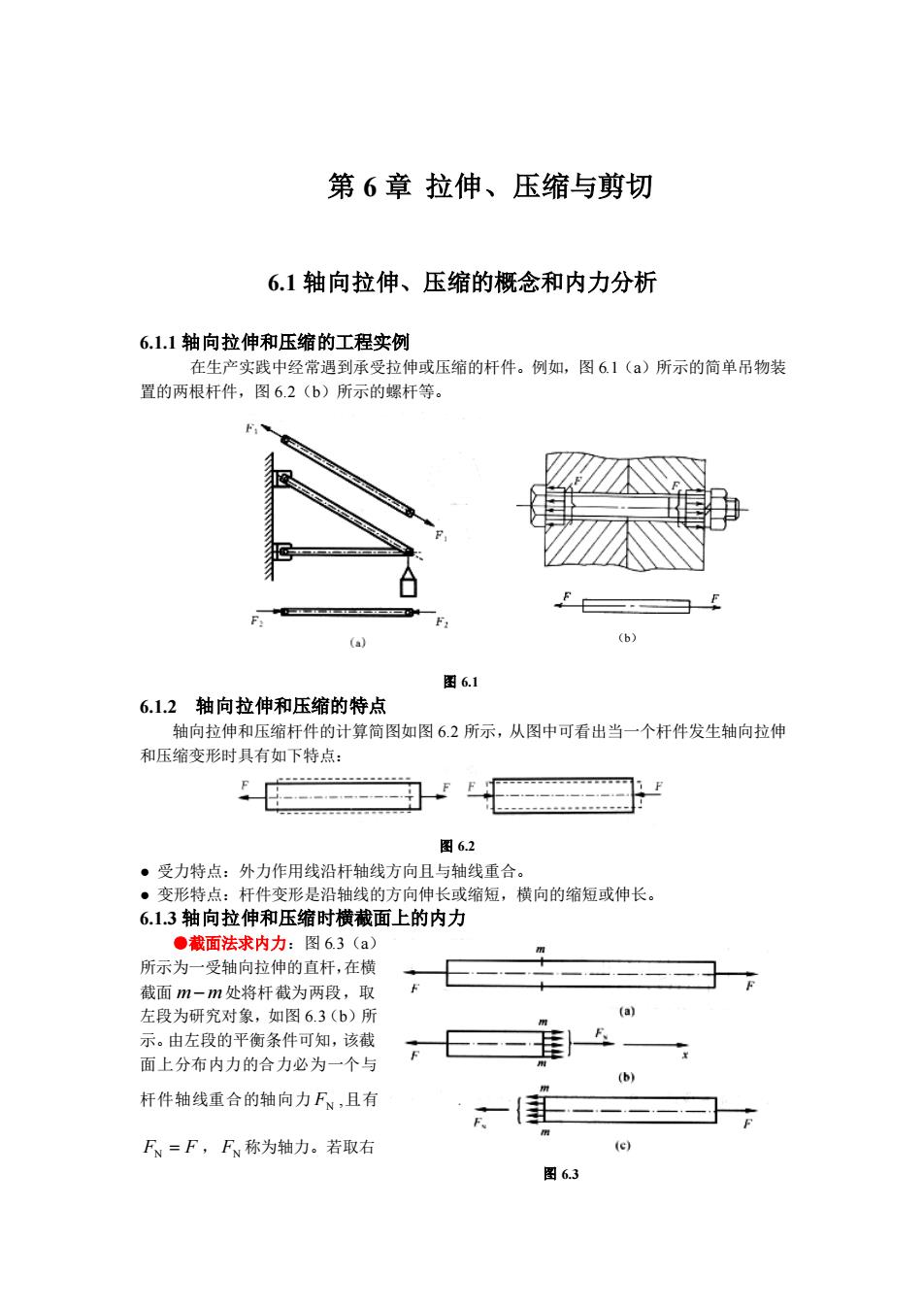
图 6.3 第 6 章 拉伸、压缩与剪切 6.1 轴向拉伸、压缩的概念和内力分析 6.1.1 轴向拉伸和压缩的工程实例 在生产实践中经常遇到承受拉伸或压缩的杆件。例如,图 6.1(a)所示的简单吊物装 置的两根杆件,图 6.2(b)所示的螺杆等。 图 6.1 6.1.2 轴向拉伸和压缩的特点 轴向拉伸和压缩杆件的计算简图如图 6.2 所示,从图中可看出当一个杆件发生轴向拉伸 和压缩变形时具有如下特点: 图 6.2 ● 受力特点:外力作用线沿杆轴线方向且与轴线重合。 ● 变形特点:杆件变形是沿轴线的方向伸长或缩短,横向的缩短或伸长。 6.1.3 轴向拉伸和压缩时横截面上的内力 ●截面法求内力:图 6.3(a) 所示为一受轴向拉伸的直杆,在横 截面 m−m 处将杆截为两段,取 左段为研究对象,如图 6.3(b)所 示。由左段的平衡条件可知,该截 面上分布内力的合力必为一个与 杆件轴线重合的轴向力 FN ,且有 FN = F , FN 称为轴力。若取右 (b)

段部分研究,如图6.3(c),则由作用力与反作用力原理知,右段截面的轴力与左段的轴力大小相等,方向相反。符号规定:为了使取左段和右段所得同一截面上的轴力不但数值相等,而且具有相同的正、负号,对轴力F正负号做如下规定:当轴力沿横截面外法线方向时,杆件的变形为轴向伸长,轴力E,为正,称为拉力:当轴力沿横截面内法线方向时,杆件的变形为轴向压缩,轴力F%为负,称为压力。轴力图:当杆件受到多个轴向外力作用时,在不同的横截面上,轴力将不相同。为了较直观地表示各横截面上的轴力,常用轴力图来表示。即用平行于杆件轴线的坐标表示横截面的位置,用垂直于杆轴线的坐标表示横截面上轴力的数值,从而绘出表示轴力与截面位置关系的图线,称为轴力图。画轴力图时,有时不需要画出坐标轴,只需标明正、负号即可。【例6-1】试画出图6.4(a)所示杆的轴力图。已知F =80kN,Fz=50kN,F,=30kN。by4R田图 6.4 解:(1)先求约束反力FA。以整个杆研究,受力如图6.4(a),列平静方程ZX=0,-FA+F-F +F, =0得FA=F-F +F =80- 50+30=60kN(2)以力作用点作为分界点,将杆分为AB、BC和CD三段,逐段计算轴力。先将杆沿横截面1-1截开,取左段(图6.4(b))列平衡方程ZX = 0,-Fa +Fni =0得FNi=FA=60kN结果为正,轴力均为拉力
段部分研究,如图 6.3(c),则由作用力与反作用力原理知,右段截面的轴力与左段的轴力 大小相等,方向相反。 ●符号规定:为了使取左段和右段所得同一截面上的轴力不但数值相等,而且具有相 同的正、负号,对轴力 FN 正负号做如下规定:当轴力沿横截面外法线方向时,杆件的变形 为轴向伸长,轴力 FN 为正,称为拉力;当轴力沿横截面内法线方向时,杆件的变形为轴向 压缩,轴力 FN 为负,称为压力。 ●轴力图:当杆件受到多个轴向外力作用时,在不同的横截面上,轴力将不相同。为 了较直观地表示各横截面上的轴力,常用轴力图来表示。即用平行于杆件轴线的坐标表示横 截面的位置,用垂直于杆轴线的坐标表示横截面上轴力的数值,从而绘出表示轴力与截面位 置关系的图线,称为轴力图。画轴力图时,有时不需要画出坐标轴,只需标明正、负号即可。 【例 6-1】试画出图 6.4(a)所示杆的轴力图。已知 F1 = 80kN,F2 = 50kN,F3 = 30kN 。 图 6.4 解:(1)先求约束反力 FA 。以整个杆研究,受力如图 6.4(a),列平静方程 X = 0,−FA + F1 − F2 + F3 = 0 得 FA = F1 − F2 + F3 = 80 − 50 + 30 = 60kN (2)以力作用点作为分界点,将杆分为 AB 、 BC 和 CD 三段,逐段计算轴力。 先将杆沿横截面 1-1 截开,取左段(图 6.4(b))列平衡方程 X = 0,−FA + FN1 = 0 得 FN1 = FA = 60kN 结果为正,轴力均为拉力

显然,在AB段各横截面上的轴力都相同,均为60kN的拉力。再将杆沿横截面2-2截开,取其左段(图6.4(c)列平衡方程ZX=0,-F +F +F2 =0得 Fn2=FA-F =60-80=-20kN结果为负,说明实际指向与假设的指向相反,指向横截面,故轴力Fz,为压力。最后将杆再沿横截面3-3截开,仍取左段(图6.4(d))列平衡方程ZX=0,-F +F-F +Fn =0得Fns =FA -F +F, =60-80+50=30kNFN3为正是拉力。(3)绘轴力图如图6.4(e)所示。本题可以不必先求出约束反力,而直接由右向左逐段求轴力,较上述求解过程简便由此题可看出,在画一个杆件某横截面的轴力时,在不知道轴力为拉力还是压力的情况下,首先假定轴力为拉力,即为正的。这样计算出的结果的正负号就是所规定的符号。【例6-2】图6.5(a)所示为一厂房的柱子,由两段等直杆组成。柱受屋架的载荷P=1000kN和两边吊车的载荷P,=80kN的作用。求柱在横截面1-1和2-2上的轴力,并作轴力图。UKN产81(0图6.5解:(1)求柱子所受的约束反力,见图6.5(b)所示由ZY=0得F=P+2P,=260kN;(2)求轴力求横截面1-1处的轴力时,沿1-1处截开,取上段研究,如图6.5(c),列平衡方程ZY=0 得 Fi=P=100kN
显然,在 AB 段各横截面上的轴力都相同,均为 60kN 的拉力。 再将杆沿横截面 2-2 截开,取其左段(图 6.4(c))列平衡方程 X = 0,−FA + F1 + FN2 = 0 得 FN2 = FA − F1 = 60 −80 = −20kN 结果为负,说明实际指向与假设的指向相反,指向横截面,故轴力 FN2 为压力。 最后将杆再沿横截面 3-3 截开,仍取左段(图 6.4(d))列平衡方程 X = 0,−FA + F1 − F2 + FN3 = 0 得 FN3 = FA − F1 + F2 = 60 −80 + 50 = 30kN FN3 为正是拉力。 (3)绘轴力图如图 6.4(e)所示。 本题可以不必先求出约束反力,而直接由右向左逐段求轴力,较上述求解过程简便。 由此题可看出,在画一个杆件某横截面的轴力时,在不知道轴力为拉力还是压力的情 况下,首先假定轴力为拉力,即为正的。这样计算出的结果的正负号就是所规定的符号。 【例 6-2】图 6.5(a)所示为一厂房的柱子,由两段等直杆组成。柱受屋架的载荷 P1 =1000kN 和两边吊车的载荷 P2 = 80kN 的作用。求柱在横截面 1-1 和 2-2 上的轴力,并作轴力图。 图 6.5 解:(1)求柱子所受的约束反力,见图 6.5(b)所示, 由 Y = 0 得 FC = P1 + 2P2 = 260kN ; (2)求轴力 求横截面 1-1 处的轴力时,沿 1-1 处截开,取上段研究,如图 6.5(c),列平衡方程 Y = 0 得 FN1 = P1 =100kN

图中轴力假设为压力,所求结果虽然是正值,但应是负值;求横截面2-2处的轴力时,沿2-2处截开,取上段研究,如图6.5(d),列平衡方程ZY=0得FN2=P+2P, =260kN同前面一样,是压力,取负值。当然也可取其下段研究,如图6.25(e),列平衡方程ZY=0 得 Fn2=Fe=260kN。(3)画柱子轴力图。如图6.5(f)。6.2轴向拉伸和压缩时横截面上的应力根据截面法求解各个截面上的轴力后,讨论拉压杆横截面上的应力。6.2.1变形现象和平面假设为了研究轴向拉伸和压缩时杆件横截面上的应力现做如下实验。取一等直杆,实验前在其表面上画出许多纵向线和横向线,如图6.6(a)所示。然后在杆的两端加一对轴向拉力F,使杆发生轴向拉伸变形。观察变形现象可以发现,变形后所有的纵向线仍为平行于轴线的直线,且相邻横向线间的纵向线伸长都相等;所有的横向线仍为垂直于轴线的直线,如图6.6(b)所示。由表及里,可以想象内部变形也是这样。于是,我们可做如下平面假设:变形前的横截面,在变形后仍保持为平面,且仍垂直于轴线。平面假设是材料力学的一个重要假设。+图 6.66.2.2应力分布规律相邻两横截面间的各纵向线伸长变形相同。根据连续均匀性假设,同一种性质的材料产生相同变形的受力必相等,即应力是均匀分布的,且垂直于横截面,如图6.6(c)所示。所以,在轴向拉伸和压缩杆件的横截面上只存在正应力,且正应力是均匀分布的。6.2.3应力计算公式根据内力和应力的关系,横截面上轴力等于横截面上均匀分布的应力的合力,于是可得F = JpdA = αA4(6-1)
图中轴力假设为压力,所求结果虽然是正值,但应是负值; 求横截面 2-2 处的轴力时,沿 2-2 处截开,取上段研究,如图 6.5(d),列平衡方程 Y = 0 得 FN2 = P1 + 2P2 = 260kN 同前面一样,是压力,取负值。 当然也可取其下段研究,如图 6.25(e),列平衡方程 Y = 0 得 FN2 = FC = 260kN 。 (3)画柱子轴力图。如图 6.5(f)。 6.2 轴向拉伸和压缩时横截面上的应力 根据截面法求解各个截面上的轴力后,讨论拉压杆横截面上的应力。 6.2.1 变形现象和平面假设 为了研究轴向拉伸和压缩时杆件横截面上的应力现做如下实验。 取一等直杆,实验前在其表面上画出许多纵向线和横向线,如图 6.6(a)所示。然后在 杆的两端加一对轴向拉力 F ,使杆发生轴向拉伸变形。观察变形现象可以发现,变形后所 有的纵向线仍为平行于轴线的直线,且相邻横向线间的纵向线伸长都相等;所有的横向线仍 为垂直于轴线的直线,如图 6.6(b)所示。由表及里,可以想象内部变形也是这样。于是, 我们可做如下平面假设:变形前的横截面,在变形后仍保持为平面,且仍垂直于轴线。平面 假设是材料力学的一个重要假设。 6.2.2 应力分布规律 相邻两横截面间的各纵向线伸长变形相同。根据连续均匀性假设,同一种性质的材料, 产生相同变形的受力必相等,即应力是均匀分布的,且垂直于横截面,如图 6.6(c)所示。 所以,在轴向拉伸和压缩杆件的横截面上只存在正应力,且正应力是均匀分布的。 6.2.3 应力计算公式 根据内力和应力的关系,横截面上轴力等于横截面上均匀分布的应力的合力,于是可得 F dA A A = = N A FN = (6-1) 图 6.6