
第9章教学方案-一弯曲变形弯曲变形概述基本内容挠曲线微分方程及其积分用叠加法求梁的位移简单静不定梁了解梁弯曲变形的工程实例,掌握挠度及转角的概念及关系。教学目2、理解挠曲线微分方程及其积分。3、熟练掌握用叠加法求梁的变形。了解简单静不定梁的求解。的重点叠加法求梁的变形。、难点
第 9 章 教学方案 ——弯曲变形 基 本 内 容 弯曲变形概述 挠曲线微分方程及其积分 用叠加法求梁的位移 简单静不定梁 教 学 目 的 1、了解梁弯曲变形的工程实例,掌握挠度及转角的概念及关系。 2、理解挠曲线微分方程及其积分。 3、熟练掌握用叠加法求梁的变形。 4、了解简单静不定梁的求解。 重 点 、 难 点 叠加法求梁的变形
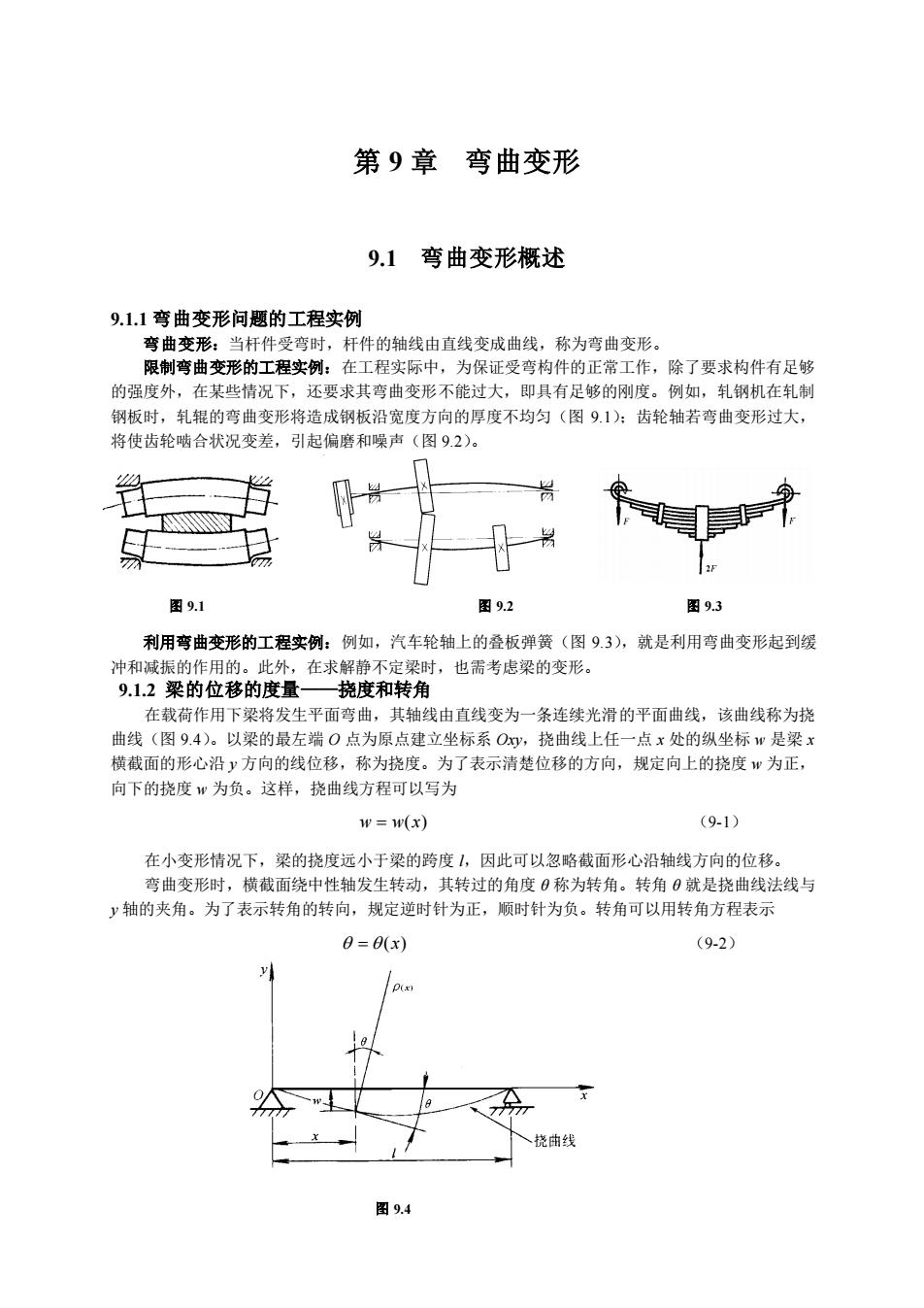
第9章弯曲变形弯曲变形概述9.19.1.1 弯曲变形问题的工程实例弯曲变形:当杆件受弯时,杆件的轴线由直线变成曲线,称为弯曲变形。限制弯曲变形的工程实例:在工程实际中,为保证受弯构件的正常工作,除了要求构件有足够的强度外,在某些情况下,还要求其弯曲变形不能过大,即具有足够的刚度。例如,轧钢机在轧制钢板时,轧辊的弯曲变形将造成钢板沿宽度方向的厚度不均匀(图9.1);齿轮轴若弯曲变形过大,将使齿轮啮合状况变差,引起偏磨和噪声(图9.2)。I-十十12F图 9.图9.3利用弯曲变形的工程实例:例如,汽车轮轴上的叠板弹簧(图9.3),就是利用弯曲变形起到缓冲和减振的作用的。此外,在求解静不定梁时,也需考虑梁的变形。9.1.2 梁的位移的度量一一度和转角在载荷作用下梁将发生平面弯曲,其轴线由直线变为一条连续光滑的平面曲线,该曲线称为挠曲线(图9.4)。以梁的最左端O点为原点建立坐标系Oxy,曲线上任一点x处的纵坐标w是梁x横截面的形心沿方向的线位移,称为挠度。为了表示清楚位移的方向,规定向上的挠度w为正,向下的挠度w为负。这样,挠曲线方程可以写为w=w(x)(9-1)在小变形情况下,梁的挠度远小于梁的跨度1,因此可以忽略截面形心沿轴线方向的位移弯曲变形时,横截面绕中性轴发生转动,其转过的角度0称为转角。转角0就是挠曲线法线与y轴的夹角。为了表示转角的转向,规定逆时针为正,顺时针为负。转角可以用转角方程表示0= 0(x)(9-2)O18挠曲线图9.4
图 9.1 图 9.2 图 9.3 第 9 章 弯曲变形 9.1 弯曲变形概述 9.1.1 弯曲变形问题的工程实例 弯曲变形:当杆件受弯时,杆件的轴线由直线变成曲线,称为弯曲变形。 限制弯曲变形的工程实例:在工程实际中,为保证受弯构件的正常工作,除了要求构件有足够 的强度外,在某些情况下,还要求其弯曲变形不能过大,即具有足够的刚度。例如,轧钢机在轧制 钢板时,轧辊的弯曲变形将造成钢板沿宽度方向的厚度不均匀(图 9.1);齿轮轴若弯曲变形过大, 将使齿轮啮合状况变差,引起偏磨和噪声(图 9.2)。 利用弯曲变形的工程实例:例如,汽车轮轴上的叠板弹簧(图 9.3),就是利用弯曲变形起到缓 冲和减振的作用的。此外,在求解静不定梁时,也需考虑梁的变形。 9.1.2 梁的位移的度量——挠度和转角 在载荷作用下梁将发生平面弯曲,其轴线由直线变为一条连续光滑的平面曲线,该曲线称为挠 曲线(图 9.4)。以梁的最左端 O 点为原点建立坐标系 Oxy,挠曲线上任一点 x 处的纵坐标 w 是梁 x 横截面的形心沿 y 方向的线位移,称为挠度。为了表示清楚位移的方向,规定向上的挠度 w 为正, 向下的挠度 w 为负。这样,挠曲线方程可以写为 w = w(x) (9-1) 在小变形情况下,梁的挠度远小于梁的跨度 l,因此可以忽略截面形心沿轴线方向的位移。 弯曲变形时,横截面绕中性轴发生转动,其转过的角度 θ 称为转角。转角 θ 就是挠曲线法线与 y 轴的夹角。为了表示转角的转向,规定逆时针为正,顺时针为负。转角可以用转角方程表示 = (x) (9-2) 图 9.4

9.1.3挠度和转角的关系弯曲变形用挠度w和转角0这两个位移量来度量。由图9.4可以看出,转角与挠曲线在该点的切线倾角相等。在小变形情况下0= tano- dw(9-3)dx即横截面的转角可以用该点处挠曲线切线的斜率表示。只要知道挠曲线方程,就能确定梁上任横截面的挠度和转角9.1.4梁的刚度条件在工程实际中,为了保证弯曲杆件的正常工作,有时会限定梁的最大挠度和最大转角,得到刚度条件l [ (9-4)jo [0] 式中,[和[]分别为许用挠度和许用转角。9.2挠曲线微分方程及其积分9.2.1挠曲线微分方程在纯弯曲时,挠曲线曲率1/p与弯矩M的关系为式(8-1),即I_MP"EI在横力弯曲时,如果是细长梁,剪力对变形的影响可以忽略,上式仍然成立,但曲率和弯矩都是x的函数,即M(a)(a)p()"EIw=w(x)上任一点的曲率为S(b)p()"())一
9.1.3 挠度和转角的关系 弯曲变形用挠度 w 和转角 θ 这两个位移量来度量。由图 9.4 可以看出,转角θ与挠曲线在该点 的切线倾角相等。在小变形情况下 x w d d tan = (9-3) 即横截面的转角可以用该点处挠曲线切线的斜率表示。只要知道挠曲线方程,就能确定梁上任 一横截面的挠度和转角。 9.1.4 梁的刚度条件 在工程实际中,为了保证弯曲杆件的正常工作,有时会限定梁的最大挠度和最大转角,得到刚 度条件 max max w f (9-4) 式中,[f]和[θ]分别为许用挠度和许用转角。 9.2 挠曲线微分方程及其积分 9.2.1 挠曲线微分方程 在纯弯曲时,挠曲线曲率 1/ρ 与弯矩 M 的关系为式(8-1),即 EI M = 1 在横力弯曲时,如果是细长梁,剪力对变形的影响可以忽略,上式仍然成立,但曲率和弯矩都是 x 的函数,即 ( ) ( ) EI M x x = 1 (a) w = w(x) 上任一点的曲率为 ( ) 2 3 2 2 2 d d 1 d d 1 + = x w x w x (b)

(b)图9.5d"w_M(d)(c)根据弯矩11EI的待号规定和接曲线二阶导数与曲率中心方位的关系,在所取坐标系下等能M的正负号始终与的正负号一致d'w_M(a)(9-5)dx?EI式(9-5)即为梁的挠曲线微分方程。9.2.2挠曲线微分方程的积分对式(9-5)积分一次,得转角方程o-dw-[兰dx+c(9-6a)Ldx再积分一次。可得曲线方程Mdxdx+Cx+L(9-6b)式中C、D为积分常数。为等截面梁时,EI为常数,可以提到积分符号外面。如果梁的弯矩方程是分段函数,则上面的积分式也应分段积分。9.2.3积分常数的确定积分常数C和D可以通过梁上某些位置的已知挠度和转角或应满足的变形关系来确定。支承条件:支座处的挠度或转角是已知的。例如铰支座处的挠度为零,,则在图9.6(a)中,在=0和x=l处,w=W,=0:又如固定端约束处的度和转角均为零,则在图9.6(b)中,在x=0处WA=0、OA=0。只要将这些数据代入式(9-6)中就可确定 C和 D。3=8ARFi(a)(b)A图 9.6图9.7
图 9.5 图 9.7 ( ) EI M x x w = 2 2 d d (c)根据弯矩 的符号规定和挠曲线二阶导数与曲率中心方位的关系,在所取坐标系下弯矩 M 的正负号始终与 2 2 d d x w 的正负号一致 ( ) EI M x x w = 2 2 d d (9-5) 式(9-5)即为梁的挠曲线微分方程。 9.2.2 挠曲线微分方程的积分 对式(9-5)积分一次,得转角方程 x C EI M x w = = + d d d (9-6a) 再积分—次.可得挠曲线方程 x x Cx D EI M w + + = d d (9-6b) 式中 C、D 为积分常数。当梁为等截面梁时,EI 为常数,可以提到积分符号外面。如果梁的弯矩方 程是分段函数,则上面的积分式也应分段积分。 9.2.3 积分常数的确定 积分常数 C 和 D 可以通过梁上某些位置的已知挠度和转角或应满足的变形关系来确定。 支承条件:支座处的挠度或转角是已知的。例如铰支座处的挠度为零,则在图 9.6(a)中,在 x=0 和 x=l 处,wA=wB=0;又如固定端约束处的挠度和转角均为零,则在图 9.6(b)中,在 x=0 处, wA=0、θA=0。只要将这些数据代入式(9-6)中就可确定 C 和 D。 图 9.6

连续光滑条件:因为挠曲线是一条连续光滑的曲线,所以在梁的积分分段点处,通过左右两段弯矩方程积分算出的挠度和转角是相等的。例如图9.7所示梁在集中力F作用点A处,有连续光滑条件为WA左-WA右和OA左=O4右。9.2.4用积分法求梁的位移对(9-5)式进行积分,并根据约束条件和连续光滑条件确定积分常数,再将已确定的积分常数代回积分式,即可得到梁的挠曲线方程和转角方程,从而可确定任一截面的挠度及转角。这种求梁的位移的方法称为积分法在工程计算中,习惯用,表示梁特定截面处的挠度。【例9-1】简支梁AB受均布载荷g作用,如图9.8所示。建立梁的挠曲线方程和转角方程,并计算最大挠度和最大转角。解:(1)计算支反力,列弯矩方程和挠曲线微分方程通过平衡方程可得Fg=Fag =%lTTTTITTT弯矩方程为fmaxqlrM(x)= Fa,x-q图 9.8故挠曲线微分方程为d?w9.(x-x)dx?=2EI(2)对挠曲线微分方程积分将上式积分两次,得o-dwq(x2x)dx2EI23g (_)+Cx+D和2Ei(612)(3)确定积分常数将约束条件x-0处W=0和x=I处W=0代入上式中,可得D=0, 和C =- 9l324F(4)建立曲线方程和转角方将C、D值代入积分式,分别得到挠曲线方程和转角方程9.(21x3 -xt -13x)W=24E0 - 4 (6-4-)(5)计算最大挠度和最大转角全梁上的弯矩都为正,所以梁的挠曲线是一条上凹的曲线,又根据结构和载荷的对称性,可画
图 9.8 连续光滑条件:因为挠曲线是一条连续光滑的曲线,所以在梁的积分分段点处,通过左右两段 弯矩方程积分算出的挠度和转角是相等的。例如图 9.7 所示梁在集中力 F 作用点 A 处,有连续光滑 条件为 wA 左=wA 右和 θA 左=θA 右。 9.2.4 用积分法求梁的位移 对(9-5)式进行积分,并根据约束条件和连续光滑条件确定积分常数,再将已确定的积分常数 代回积分式,即可得到梁的挠曲线方程和转角方程,从而可确定任一截面的挠度及转角。这种求梁 的位移的方法称为积分法。 在工程计算中,习惯用 f 表示梁特定截面处的挠度。 【例 9-1】简支梁 AB 受均布载荷 q 作用,如图 9.8 所示。建立梁的挠曲线方程和转角方程,并 计算最大挠度和最大转角。 解:(1)计算支反力,列弯矩方程和挠曲线微分方程 通过平衡方程可得 2 ql FAy = FBy = 弯矩方程为 故挠曲线微分方程为 ( ) d 2 d 2 2 2 lx x EI q x w = − (2)对挠曲线微分方程积分 将上式积分两次,得 C lx x EI q x w + = = − d 2 2 3 d 2 3 和 Cx D lx x EI q w + + = − 2 6 12 3 4 (3)确定积分常数 将约束条件 x=0 处 w=0 和 x=l 处 w=0 代入上式中,可得 D=0,和 EI ql C 24 3 = − (4)建立挠曲线方程和转角方程 将 C、D 值代入积分式,分别得到挠曲线方程和转角方程 ( ) ( ) 2 3 3 3 4 3 6 4 24 2 24 lx x l EI q lx x l x EI q w = − − = − − (5)计算最大挠度和最大转角 全梁上的弯矩都为正,所以梁的挠曲线是一条上凹的曲线,又根据结构和载荷的对称性,可画 2 2 2 ( ) 2 qx x x ql M x F x qx = Ay − = −