
第3章教学方案一平面任意力系力线平移定理基本内容平面任意力系的简化平面任意力系的平衡条件和平衡方程物体系统的平衡考虑摩擦时的平衡问题掌握力线平移定理。教学目的了解平面力系向一点简化。、熟练掌握平面力系的平衡方程。掌握物体系统的平衡问题分析。了解有摩擦时物体的平衡分析。重点、难点平面力系的简化:物体系统的平衡问题
第 3 章 教学方案 ——平面任意力系 基 本 内 容 力线平移定理 平面任意力系的简化 平面任意力系的平衡条件和平衡方程 物体系统的平衡 考虑摩擦时的平衡问题 教 学 目 的 1、掌握力线平移定理。 2、了解平面力系向一点简化。 3、熟练掌握平面力系的平衡方程。掌握物体系统的平衡问题分 析。了解有摩擦时物体的平衡分析。 重 点 、 难 点 平面力系的简化;物体系统的平衡问题
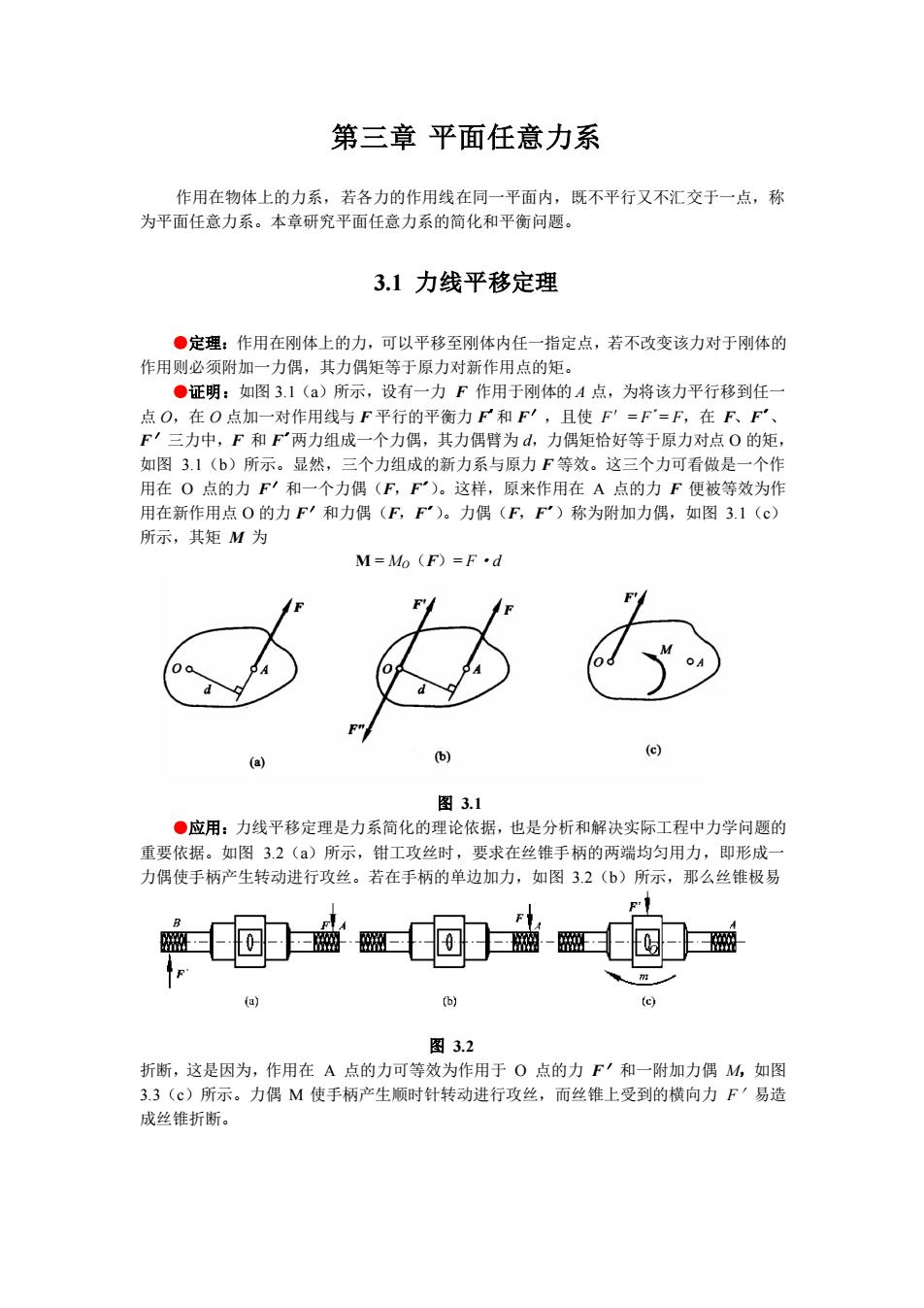
第三章平面任意力系作用在物体上的力系,若各力的作用线在同一平面内,既不平行又不汇交于一点,称为平面任意力系。本章研究平面任意力系的简化和平衡问题。3.1力线平移定理定理:作用在刚体上的力,可以平移至刚体内任一指定点,若不改变该力对于刚体的作用则必须附加一力偶,其力偶矩等于原力对新作用点的矩。证明:如图3.1(a)所示,设有一力F作用于刚体的4点,为将该力平行移到任点 O,在 O 点加一对作用线与 F平行的平衡力 F 和 F",且使 FI =F'=F,在 F、F'F'三力中,F和F两力组成一个力偶,其力偶臂为d,力偶矩恰好等于原力对点O的矩如图3.1(b)所示。显然,三个力组成的新力系与原力F等效。这三个力可看做是一个作用在O点的力F'和一个力偶(F,F")。这样,原来作用在A点的力F便被等效为作用在新作用点O的力F/和力偶(F,F")。力偶(F,F")称为附加力偶,如图3.1(c)所示,其矩M为M=MoCF)()(b)(a图 3.1·应用:力线平移定理是力系简化的理论依据,也是分析和解决实际工程中力学问题的重要依据。如图3.2(a)所示,钳工攻丝时,要求在丝锥手柄的两端均匀用力,即形成一力偶使手柄产生转动进行攻丝。若在手柄的单边加力,如图3.2(b)所示,那么丝锥极易Ft中a(b)(c)图3.2折断,这是因为,作用在A点的力可等效为作用于 O点的力F和一附加力偶M,如图3.3(c)所示。力偶M使手柄产生顺时针转动进行攻丝,而丝锥上受到的横向力F'易造成丝锥折断
第三章 平面任意力系 作用在物体上的力系,若各力的作用线在同一平面内,既不平行又不汇交于一点,称 为平面任意力系。本章研究平面任意力系的简化和平衡问题。 3.1 力线平移定理 ●定理:作用在刚体上的力,可以平移至刚体内任一指定点,若不改变该力对于刚体的 作用则必须附加一力偶,其力偶矩等于原力对新作用点的矩。 ●证明:如图 3.1(a)所示,设有一力 F 作用于刚体的 A 点,为将该力平行移到任一 点 O,在 O 点加一对作用线与 F 平行的平衡力 F 〃和 F′,且使 F′= F 〃 = F,在 F、F 〃 、 F′三力中,F 和 F 〃 两力组成一个力偶,其力偶臂为 d,力偶矩恰好等于原力对点 O 的矩, 如图 3.1(b)所示。显然,三个力组成的新力系与原力 F 等效。这三个力可看做是一个作 用在 O 点的力 F′和一个力偶(F,F 〃 )。这样,原来作用在 A 点的力 F 便被等效为作 用在新作用点 O 的力 F′和力偶(F,F 〃 )。力偶(F,F 〃 )称为附加力偶,如图 3.1(c) 所示,其矩 M 为 M = MO(F)= F·d 图 3.1 ●应用:力线平移定理是力系简化的理论依据,也是分析和解决实际工程中力学问题的 重要依据。如图 3.2(a)所示,钳工攻丝时,要求在丝锥手柄的两端均匀用力,即形成一 力偶使手柄产生转动进行攻丝。若在手柄的单边加力,如图 3.2(b)所示,那么丝锥极易 图 3.2 折断,这是因为,作用在 A 点的力可等效为作用于 O 点的力 F′和一附加力偶 M,如图 3.3(c)所示。力偶 M 使手柄产生顺时针转动进行攻丝,而丝锥上受到的横向力 F′易造 成丝锥折断

3.2平面任意力系的简化3.2.1平面任意力系向平面内一点的简化●简化依据:力线平移定理。简化方法:把各力向平面内任取的一点O平移(称为简化中心),得到作用于点○的力,以及相应的附加力偶,如图3.3(b)所示。这样,平面任意力系简化成平面汇交力系和平面力偶系。分别将平面汇交力系和平面力偶系合成为一个合力和一个合力偶,如图3.3(c)所示。合力F-ZF(3-1)合力偶的矩Mo等于各力偶矩的代数和。附加力偶矩等于力对简化中心的矩,故M(3-2)1.(F)2b()图3.33.2.2主矢和主矩的概念主失和主矩:平面任意力系各力的矢量和FR,称为该力系的主失;而这些力对于简化中心O取矩的代数和Mo,称为该力系对于简化中心的主矩。主矢等于各力的矢量和,所以它与简化中心的选择无关。而主矩等于各力对简化中心的矩的代数和,取不同的点为简化中心,各力的力臂将有改变,则各力对简化中心的矩也有改变,所以在一般情况下主矩与简化中心的选择有关。应用解析法可求出力系的主失F的大小和方向。过点O取坐标系Oxy,则有FR=F2+1[Y+(ZF(3-3)cosacosβ:FR
3.2 平面任意力系的简化 3.2.1 平面任意力系向平面内一点的简化 ●简化依据:力线平移定理。 ●简化方法:把各力向平面内任取的一点 O 平移(称为简化中心),得到作用于点 O 的 力,以及相应的附加力偶,如图 3.3(b)所示。这样,平面任意力系简化成平面汇交力系 和平面力偶系。分别将平面汇交力系和平面力偶系合成为一个合力和一个合力偶,如图 3.3 (c)所示。合力 1 n i I = F F R = (3-1) 合力偶的矩 MO 等于各力偶矩的代数和。附加力偶矩等于力对简化中心的矩,故 1 1 ( ) n n o i o I I M M M = = = = Fi (3-2) 3.2.2 主矢和主矩的概念 ●主矢和主矩:平面任意力系各力的矢量和 FR ,称为该力系的主矢;而这些力对于简 化中心 O 取矩的代数和 MO,称为该力系对于简化中心的主矩。主矢等于各力的矢量和,所 以它与简化中心的选择无关。而主矩等于各力对简化中心的矩的代数和,取不同的点为简化 中心,各力的力臂将有改变,则各力对简化中心的矩也有改变,所以在一般情况下主矩与简 化中心的选择有关。 应用解析法可求出力系的主矢 FR 的大小和方向。过点 O 取坐标系 Oxy,则有 2 2 2 2 ( ) ( ) cos cos n n R Rx Ry ix iy i=1 i=1 Rx R Ry R F F F F F F F F F = + = + = = (3-3) 图 3.3
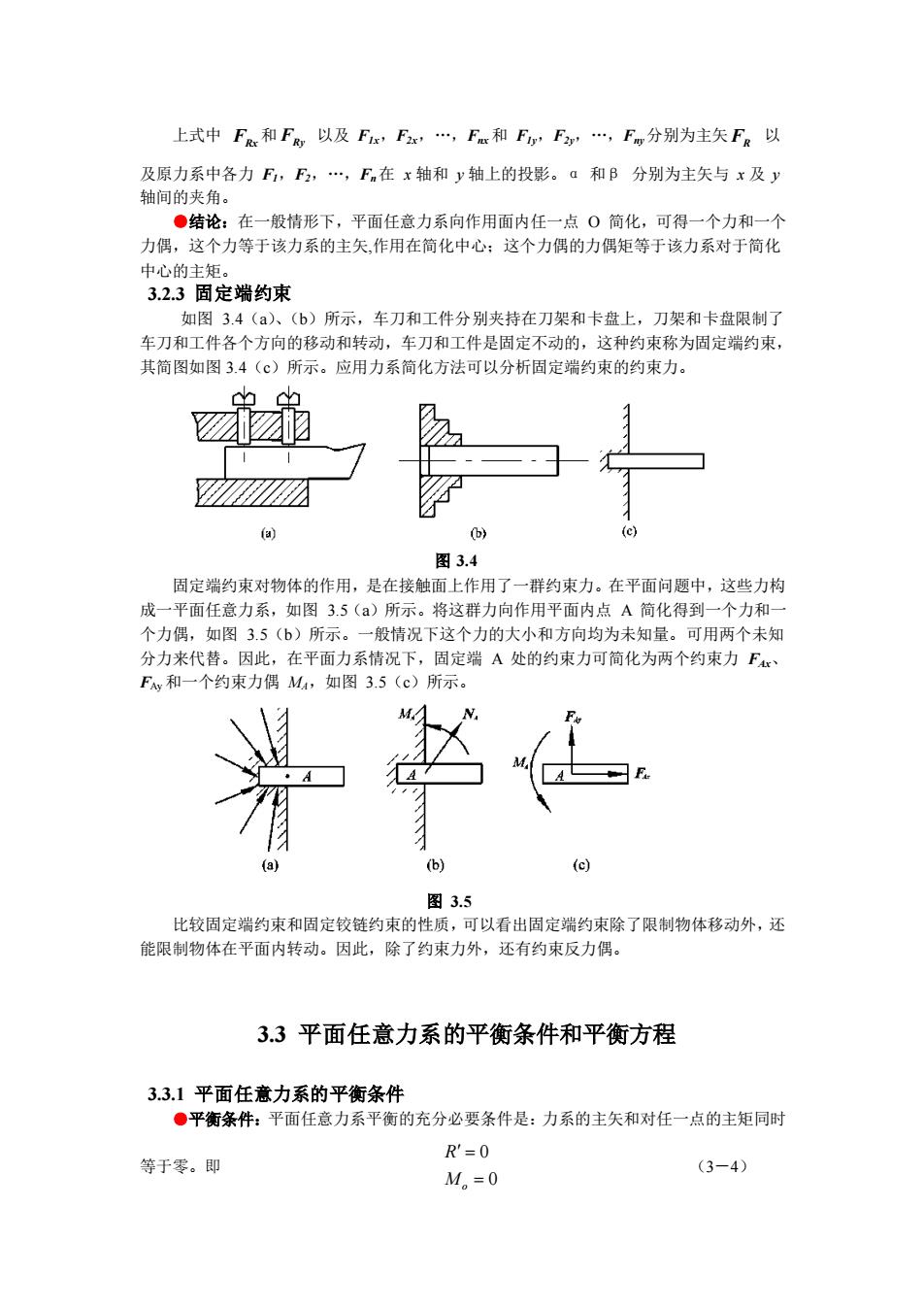
上式中F和Fry以及Fix,Fax,F和Fiy,Fay,“,Fm分别为主失FR以及原力系中各力Fi,F2,,F,在x轴和y轴上的投影。α和β分别为主矢与×及y轴间的夹角。结论:在一般情形下,平面任意力系向作用面内任一点○简化,可得一个力和一个力偶,这个力等于该力系的主矢,作用在简化中心;这个力偶的力偶矩等于该力系对于简化中心的主矩3.2.3固定端约束如图3.4(a)、(b)所示,车刀和工件分别夹持在刀架和卡盘上,刀架和卡盘限制了车刀和工件各个方向的移动和转动,车刀和工件是固定不动的,这种约束称为固定端约束,其简图如图3.4(c)所示。应用力系简化方法可以分析固定端约束的约束力。NAAAWA(a)(b)图 3.4固定端约束对物体的作用,是在接触面上作用了一群约束力。在平面问题中,这些力构成一平面任意力系,如图3.5(a)所示。将这群力向作用平面内点A简化得到一个力和一个力偶,如图3.5(b)所示。一般情况下这个力的大小和方向均为未知量。可用两个未知分力来代替。因此,在平面力系情况下,固定端A处的约束力可简化为两个约束力FAxFAy和一个约束力偶MA,如图3.5(c)所示,行(a)(b)(c)图3.5比较固定端约束和固定铰链约束的性质,可以看出固定端约束除了限制物体移动外,还能限制物体在平面内转动。因此,除了约束力外,还有约束反力偶。3.3平面任意力系的平衡条件和平衡方程3.3.1平面任意力系的平衡条件·平衡条件:平面任意力系平衡的充分必要条件是:力系的主矢和对任一点的主矩同时R'= 0等于零。即(3-4)M。=0
上式中 FRx 和 FRy 以及 F1x,F2x,.,Fnx 和 F1y,F2y,.,Fny分别为主矢 FR 以 及原力系中各力 F1,F2,.,Fn在 x 轴和 y 轴上的投影。α 和β 分别为主矢与 x 及 y 轴间的夹角。 ●结论:在一般情形下,平面任意力系向作用面内任一点 O 简化,可得一个力和一个 力偶,这个力等于该力系的主矢,作用在简化中心;这个力偶的力偶矩等于该力系对于简化 中心的主矩。 3.2.3 固定端约束 如图 3.4(a)、(b)所示,车刀和工件分别夹持在刀架和卡盘上,刀架和卡盘限制了 车刀和工件各个方向的移动和转动,车刀和工件是固定不动的,这种约束称为固定端约束, 其简图如图 3.4(c)所示。应用力系简化方法可以分析固定端约束的约束力。 图 3.4 固定端约束对物体的作用,是在接触面上作用了一群约束力。在平面问题中,这些力构 成一平面任意力系,如图 3.5(a)所示。将这群力向作用平面内点 A 简化得到一个力和一 个力偶,如图 3.5(b)所示。一般情况下这个力的大小和方向均为未知量。可用两个未知 分力来代替。因此,在平面力系情况下,固定端 A 处的约束力可简化为两个约束力 FAx、 FAy 和一个约束力偶 MA,如图 3.5(c)所示。 图 3.5 比较固定端约束和固定铰链约束的性质,可以看出固定端约束除了限制物体移动外,还 能限制物体在平面内转动。因此,除了约束力外,还有约束反力偶。 3.3 平面任意力系的平衡条件和平衡方程 3.3.1 平面任意力系的平衡条件 ●平衡条件:平面任意力系平衡的充分必要条件是:力系的主矢和对任一点的主矩同时 等于零。即 0 0 o R M = = (3-4)

所以,R'=ZF)+(ZF)=0(3-5)M,=ZM.(F)=03.3.2 平面任意力系的平衡方程根据平衡条件(3-5)式可得[F,=02F,-0(3-6)(M,(F)=0式(3-6)称为平面任意力系的平衡方程的基本形式。平面任意力系平衡方程可解三个未知力【例3-1】悬臂吊车如图3.6(a)所示。横梁AB长/=2.5m,重力W=1.2kN。拉杆CD倾角α=30°,重力不计。电葫芦连同重物重力G=7.5kN。试求当电葫芦在x=2m的位置时,拉杆的拉力F和铰链A的约束力。F公Lα(a)(h)图 3.6 解:(1)选横梁AB为研究对象,画受力图,如图3.6(b)所示。主动力:W,G:约束力:F、FAx、FAy。CD是二力杆,F沿CD连线。各力作用线在同一平面内且任意分布,属平面任意力系。(2)选图示坐标,列平衡方程求解。ZF,=0Fx-Fcosα=0ZF,=0F, +Fsinα-W-G=0[M,(F)=0 FIsinα-W1-Gx=0解得
所以, 2 2 ( ) ( ) 0 ( ) 0 x y o o R F F M M F = + = = = (3-5) 3.3.2 平面任意力系的平衡方程 根据平衡条件(3-5)式可得 0 0 ( ) 0 x y o F F M F = = = (3-6) 式(3-6)称为平面任意力系的平衡方程的基本形式。平面任意力系平衡方程可解三个 未知力。 【例 3-1】悬臂吊车如图 3.6(a)所示。横梁 AB 长 l=2.5m,重力 W=1.2kN。拉杆 CD 倾角α=30°,重力不计。电葫芦连同重物重力 G=7.5kN。试求当电葫芦在 x =2m 的位置 时,拉杆的拉力 F 和铰链 A 的约束力。 (a) (b) 图 3.6 解: (1)选横梁 AB 为研究对象,画受力图,如图 3.6(b)所示。 主动力: W , G;约束力: F 、FAx、FAy。CD 是二力杆, F 沿 CD 连线。各力 作用线在同一平面内且任意分布,属平面任意力系。 (2)选图示坐标,列平衡方程求解。 0 cos 0 0 sin 0 ( ) 0 sin 0 2 x Ax y Ay A F F F F F F W G l M F Fl W Gx = − = = + − − = = − − = 解得