
第十三章能量法2S13-1 概述在弹性范围内,弹性体在外力作用下发生变形而在体内积蓄的能量,称为弹性应变能,简称应变能。物体在外力作用下发生变形,物体的变形能在数值上等于外力在加载过程中在相应位移上所做的功,即V.-w
第十三章 能量法 §13-1 概 述 在弹性范围内,弹性体在外力作用下发生 变形而在体内积蓄的能量,称为弹性应变能, 简称应变能。 物体在外力作用下发生变形,物体的变形 能在数值上等于外力在加载过程中在相应位移 上所做的功,即 V =W

S 13-2 杆件变形能计算一、轴向拉伸和压缩FF?21F12EA 2EAFN(x)FNNdx2EA(x)
§13-2 杆件变形能计算 一、轴向拉伸和压缩 V = W F F l l = F l 2 1 EA Fl F 2 1 = EA F l EA F l N 2 2 2 2 = = = l N x EA x F x V d 2 ( ) ( ) 2
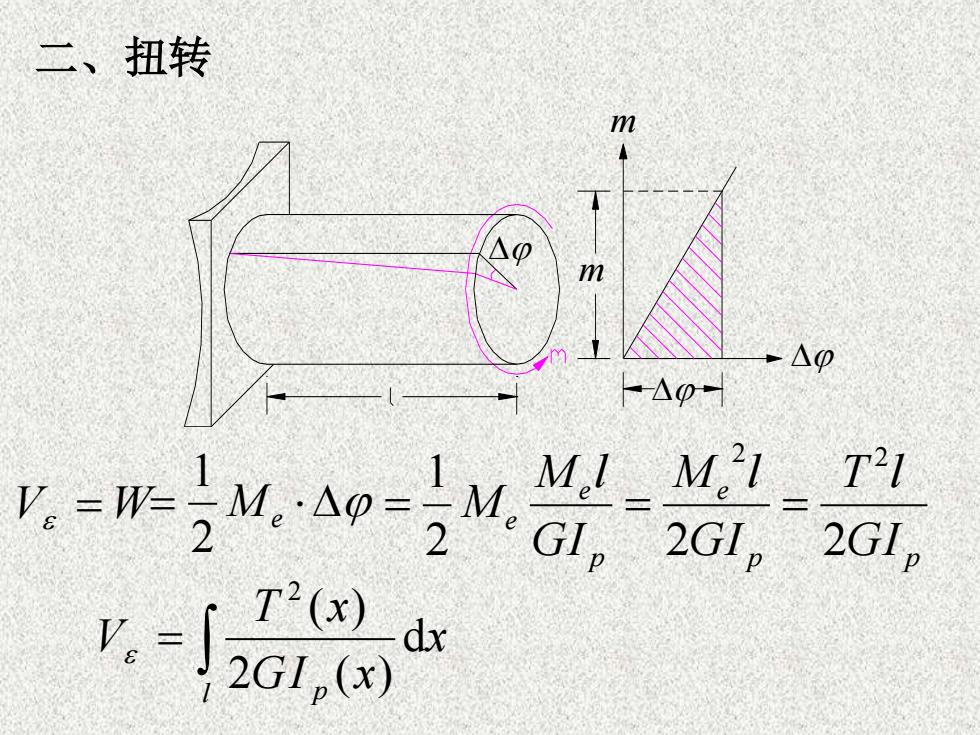
二、 扭转mmApNp-M,1 M1 T?1V, = W-I M.Aβ--IM2GI2GI。2GIT?(x)dx2GI,(x)
二、扭转 V = W m m = Me 2 1 p p e p e e GI T l GI M l GI M l M 2 2 2 1 2 2 = = = = l p x GI x T x V d 2 ( ) ( ) 2

三、弯曲V.=WM21M?1M.1福浴1纯弯曲:=M·0=M2EI2E12EI2M2(x)横力弯曲:V=dx2EI(x)
三、弯曲 V = W 纯弯曲: 横力弯曲: = l x EI x M x V d 2 ( ) ( ) 2 = Me 2 1 EI M l M e e 2 1 = EI M l EI M l e 2 2 2 2 = =
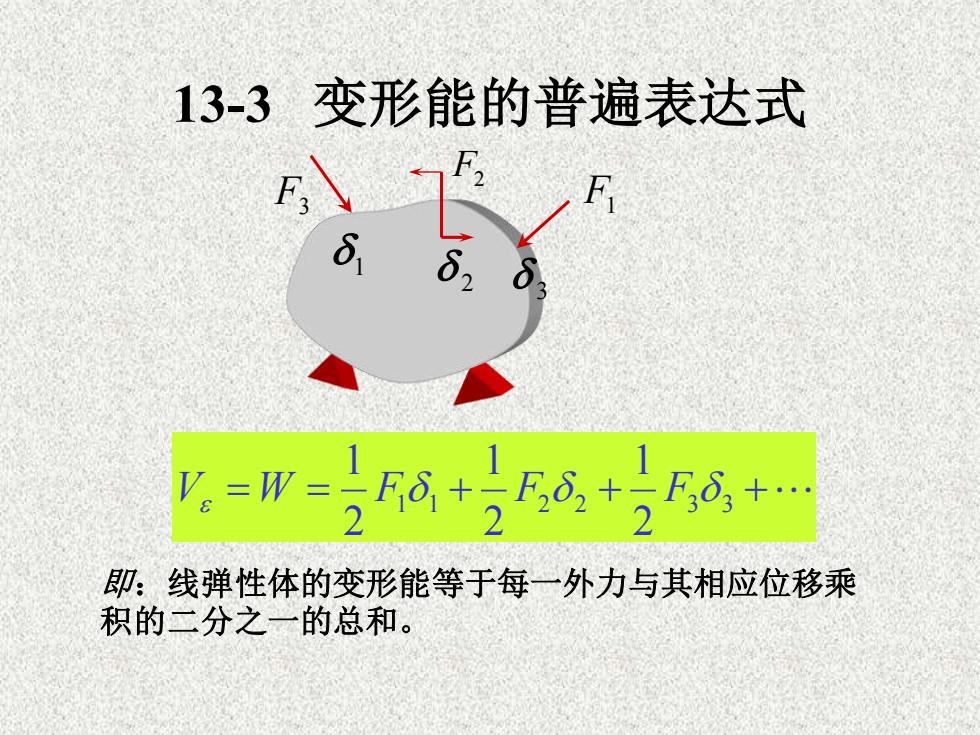
13-3变形能的普遍表达式F2FFS.828=-F8+=12 +=F8,+H即:线弹性体的变形能等于每一外力与其相应位移乘积的二分之一的总和
13-3 变形能的普遍表达式 F1 F2 F3 1 2 3 = = 1 1 + 2 2 + 3 3 + 2 1 2 1 2 1 V W F F F 即:线弹性体的变形能等于每一外力与其相应位移乘 积的二分之一的总和