
第1章 教学方案 一一静力学基本概念和受力分析 基本内容 静力学基本概念: 静力学公理: 约束与约束反力: 物体的受力分析和受力图。 【、理解刚体力学模型的建立:掌握平衡的概念:掌握力的三个要 素。 教学目的 2、 掌握二力平衡条件、三力平衡汇交条件和加减平衡力系原理 3 熟练掌握各种约束及约束反力的画法 4、熟练掌握对机构及构件进行受力分析并画受力图。 重 、难点 物体的受力分析及受力图
第 1 章 教学方案 ——静力学基本概念和受力分析 基 本 内 容 静力学基本概念; 静力学公理; 约束与约束反力; 物体的受力分析和受力图。 教 学 目 的 1、理解刚体力学模型的建立;掌握平衡的概念;掌握力的三个要 素。 2、掌握二力平衡条件、三力平衡汇交条件和加减平衡力系原理。 3、熟练掌握各种约束及约束反力的画法。 4、熟练掌握对机构及构件进行受力分析并画受力图。 重 点 、 难 点 物体的受力分析及受力图

第一章静力学基本概念和受力分析1.1静力学基本概念1.1.1刚体的概念刚体:指受力后不变形的物体。这是个理想化的力学模型。如果变形是微小的,对研究物体的平衡问题不起主要作用,就可以将其看成刚体,使问题的研究大为简化。力学模型的选用并不是唯一的:与所研究问题的性质密切相关,当研究工程构件受力后的变形和破坏规律时,即使变形量很小也必须将构件简化为变形固体。静力学研究的物体只限于刚体,故又称刚体静力学,它是研究变形体力学的基础1.1.2 力的概念·力的定义:力是物体间相互的机械作用,这种作用使物体产生两种效应:一是物体运动状态的改变,称为力的运动效应:二是物体形状的改变,称为力的变形效应。●力的三要素:力的大小、力的方向、力的作用点,●力的矢量表示:可以用一个矢量来表示力的要素,如图1.1所示。我们常用黑体字母F表示力的矢量,而用普通字母F表示力的大小。●力的单位:在国际单位制(SI)中,是牛顿,常以符号“N”表示。有时也以千牛顿(KN)作为力的单位●力系:通常把作用在同一研究对象上的一组力称为力系。图 1.11.1.3平衡的概念平衡的概念:平衡是指物体相对于惯性参考系(如地面)保持静止或作匀速直线运动如静止的桥梁和机床的床身、作匀速直线飞行的飞机等等,都处于平衡状态·平衡条件:平衡是物体运动的一种特殊形式,当物体平衡时,其上受力必须满足一定的条件,称为平衡条件。1.2静力学公理公理是人们在长期的生活和生产实际中总结出来的、经过反复实践检验证明的、符合客观实际的最普遍和最一般的规律。1. 2. 1二力平衡公理作用在同一刚体上的两个力,使刚体处于平衡状态的必要和充分条件是;这两个力的大小相等,方向相反,且在同一直线上。如图1.2所示,即Fi=-F2(1-1)●最简单的力系平衡条件。·本公理只适用于刚体,对于变形体平衡,等值、反向、共线是必要条件,而非充分条件。例如:软绳受两个等值反向的拉力作用可以平衡,而受两个等值反向的压力作用就不能
第一章 静力学基本概念和受力分析 1.1 静力学基本概念 1.1.1 刚体的概念 ●刚体:指受力后不变形的物体。这是一个理想化的力学模型。如果变形是微小的,对 研究物体的平衡问题不起主要作用,就可以将其看成刚体,使问题的研究大为简化。 ●力学模型的选用并不是唯一的:与所研究问题的性质密切相关,当研究工程构件受 力后的变形和破坏规律时,即使变形量很小也必须将构件简化为变形固体。 静力学研究的物体只限于刚体,故又称刚体静力学,它是研究变形体力学的基础。 1.1.2 力的概念 ●力的定义:力是物体间相互的机械作用,这种作用使物体产生两种效应:一是物体运 动状态的改变,称为力的运动效应;二是物体形状的改变,称为力的变形效应。 ●力的三要素:力的大小、力的方向、力的作 用点。 ●力的矢量表示:可以用一个矢量来表示力的 三要素,如图 1.1 所示。我们常用黑体字母 F 表示 力的矢量,而用普通字母 F 表示力的大小。 ●力的单位:在国际单位制(SI)中,是牛顿, 常以符号“N”表示。有时也以千牛顿(KN)作为 力的单位。 ●力系:通常把作用在同一研究对象上的一组 力称为力系。 图 1.1 1.1.3 平衡的概念 ●平衡的概念:平衡是指物体相对于惯性参考系(如地面)保持静止或作匀速直线运动。 如静止的桥梁和机床的床身、作匀速直线飞行的飞机等等,都处于平衡状态。 ●平衡条件:平衡是物体运动的一种特殊形式,当物体平衡时,其上受力必须满足一定 的条件,称为平衡条件。 1.2 静力学公理 公理是人们在长期的生活和生产实际中总结出来的、经过反复实践检验证明的、符合客 观实际的最普遍和最一般的规律。 1.2.1 二力平衡公理 作用在同一刚体上的两个力,使刚体处于平衡状态的必要和充分条件是:这两个力的 大小相等,方向相反,且在同一直线上。如图 1.2 所示 ,即 F1= - F2 (1-1) ●最简单的力系平衡条件。 ●本公理只适用于刚体,对于变形体平衡,等值、反向、共线是必要条件,而非充分条 件。例如:软绳受两个等值反向的拉力作用可以平衡,而受两个等值反向的压力作用就不能
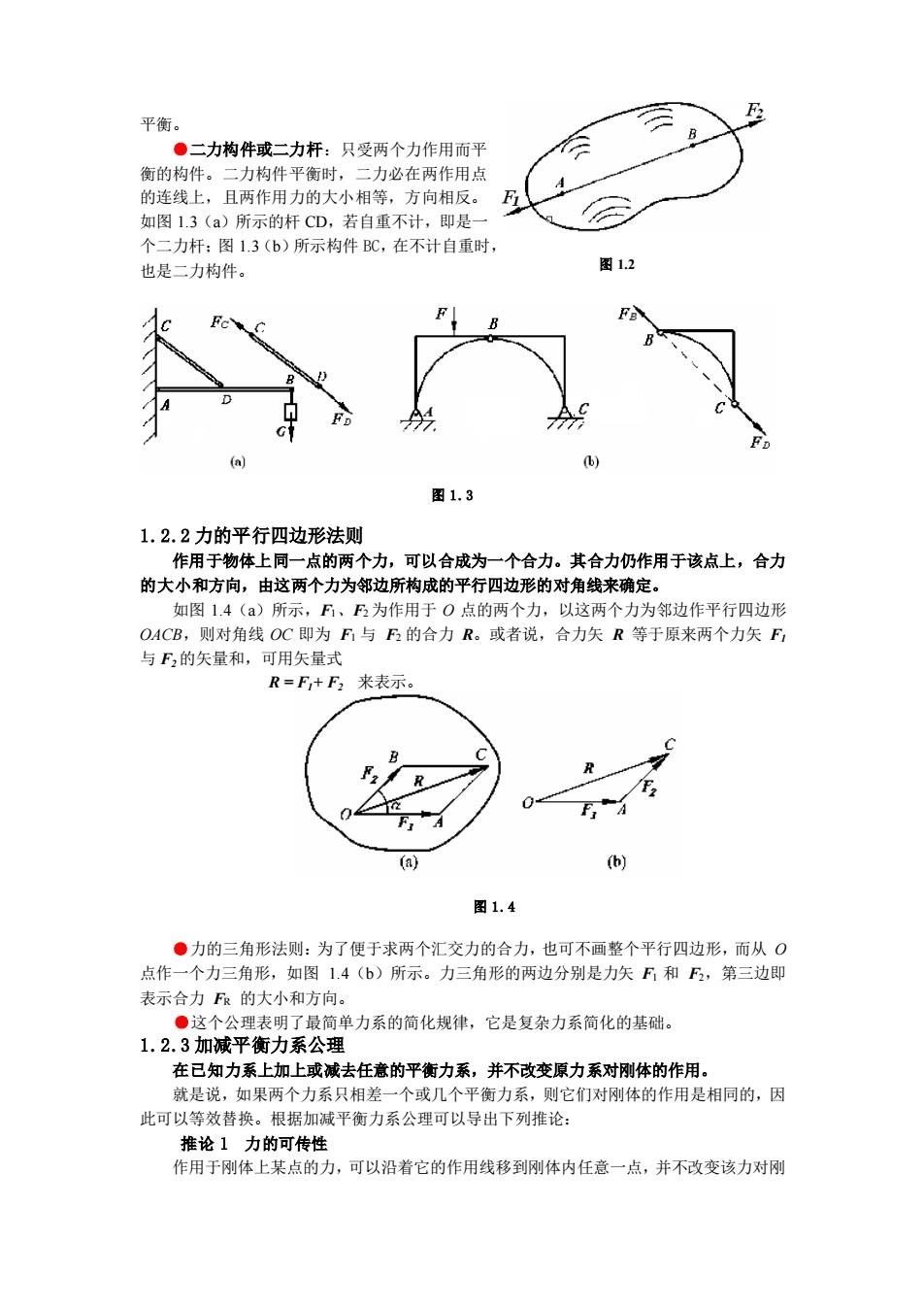
平衡●二力构件或二力杆:只受两个力作用而衡的构件。二力构件平衡时,二力必在两作用点的连线上,且两作用力的大小相等,方向相反。1如图1.3(a)所示的杆CD,若自重不计,即是个二力杆:图1.3(b)所示构件BC,在不计自重时,图1.2也是二力构件。图1.31.2.2力的平行四边形法则作用于物体上同一点的两个力,可以合成为一个合力。其合力仍作用于该点上,合力的大小和方向,由这两个力为邻边所构成的平行四边形的对角线来确定。如图1.4(a)所示,Fi、F2为作用于0点的两个力,以这两个力为邻边作平行四边形OACB,则对角线OC即为F与F2的合力R。或者说,合力失R等于原来两个力失Fi与F,的矢量和,可用矢量式R=Fi+F2来表示IF(b)图1. 4·力的三角形法则:为了便于求两个汇交力的合力,也可不画整个平行四边形,而从○点作一个力三角形,如图1.4(b)所示。力三角形的两边分别是力失F和F2,第三边即表示合力FR的大小和方向。这个公理表明了最简单力系的简化规律,它是复杂力系简化的基础。1.2.3加减平衡力系公理在已知力系上加上或减去任意的平衡力系,并不改变原力系对刚体的作用。就是说,如果两个力系只相差一个或几个平衡力系,则它们对刚体的作用是相同的,因此可以等效替换。根据加减平衡力系公理可以导出下列推论:推论 1力的可传性作用于刚体上某点的力,可以沿着它的作用线移到刚体内任意一点,并不改变该力对刚
图 1.2 图 1.4 平衡。 ●二力构件或二力杆:只受两个力作用而平 衡的构件。二力构件平衡时,二力必在两作用点 的连线上,且两作用力的大小相等,方向相反。 如图 1.3(a)所示的杆 CD,若自重不计,即是一 个二力杆;图 1.3(b)所示构件 BC,在不计自重时, 也是二力构件。 1.2.2 力的平行四边形法则 作用于物体上同一点的两个力,可以合成为一个合力。其合力仍作用于该点上,合力 的大小和方向,由这两个力为邻边所构成的平行四边形的对角线来确定。 如图 1.4(a)所示,F1、F2 为作用于 O 点的两个力,以这两个力为邻边作平行四边形 OACB,则对角线 OC 即为 F1 与 F2 的合力 R。或者说,合力矢 R 等于原来两个力矢 F1 与 F2 的矢量和,可用矢量式 R = F1+ F2 来表示。 ●力的三角形法则:为了便于求两个汇交力的合力,也可不画整个平行四边形,而从 O 点作一个力三角形,如图 1.4(b)所示。力三角形的两边分别是力矢 F1 和 F2,第三边即 表示合力 FR 的大小和方向。 ●这个公理表明了最简单力系的简化规律,它是复杂力系简化的基础。 1.2.3 加减平衡力系公理 在已知力系上加上或减去任意的平衡力系,并不改变原力系对刚体的作用。 就是说,如果两个力系只相差一个或几个平衡力系,则它们对刚体的作用是相同的,因 此可以等效替换。根据加减平衡力系公理可以导出下列推论: 推论 l 力的可传性 作用于刚体上某点的力,可以沿着它的作用线移到刚体内任意一点,并不改变该力对刚 图 1.3

体的作用。证明:设力F作用于刚体上的A点,如图1.5(a)所示。根据加减平衡力系公理,在力的作用线上任一点B加上两个相互平衡的力F和F,使F=F=-F,如图1.5(b)所示。由于力F和F也是一个平衡力系,可除去,这样只剩下一个力F,如图1.5(c)所示。于是,原来的这个力F与力系(F、FI、F)以及力F2互等。而力F2就是原来的力F,只是作用点已移到了点B。(a)(b)(c)图 1. 5 由此可见,作用于刚体上的力的三要素是:力的大小、方向和作用线。推论 2 三力平衡汇交定理刚体在三个力的作用下平衡,若其中二力作用线相交,则第三个力的作用线必过该交点且三力共面。F图1.6证明:如图1.6所示,刚体上A、B、C三点分别作用力FI、F,和F,其中F与E,的作用线相交于O点,刚体在此三力作用下处于平衡状态。根据力的可传性,将力E和F,合成得合力Ri2,则力F应与Riz平衡,因而F,必与R12共线,即F,作用线也通过O 点。另外,因为 F、F,与 R12共面,所以 F、F,与 F;也共面。于是定理得证。利用三力平衡汇交定理可以确定刚体在三力作用下平衡时未知力的方向。1.2.4作用力与反作用力定律两物体间的作用力与反作用力总是同时存在的,且两力的大小相等、方向相反、沿着同一直线,分别作用在两个相互作用的物体上。这个公理概括了物体间相互作用的关系,表明作用力和反作用力总是成对出现的。1.2.5刚化原理变形体在某一力系作用下处于平衡,如将此变形体刚化为刚体其平衡状态保持不变
体的作用。 证明:设力 F 作用于刚体上的 A 点,如图 1.5(a)所示。根据加减平衡力系公理,在 力的作用线上任一点 B 加上两个相互平衡的力 F1 和 F2,使 F = F2= - F1,如图 1.5(b)所 示。由于力 F 和 F1 也是一个平衡力系,可除去,这样只剩下一个力 F2,如图 1.5(c)所 示。于是,原来的这个力 F 与力系(F、F1、F2)以及力 F2 互等。而力 F2 就是原来的力 F, 只是作用点已移到了点 B。 由此可见,作用于刚体上的力的三要素是:力的大小、方向和作用线。 推论 2 三力平衡汇交定理 刚体在三个力的作用下平衡,若其中二力作用线相交,则第三个力的作用线必过该交点, 且三力共面。 证明:如图 1.6 所示,刚体上 A、B、C 三点分别作用力 F1、F2 和 F3,其中 F1 与 F2 的作用线相交于 O 点,刚体在此三力作用下处于平衡状态。根据力的可传性,将力 F1 和 F2 合成得合力 R12,则力 F3 应与 R12 平衡,因而 F3 必与 R12 共线,即 F3 作用线也通过 O 点。另外,因为 F1、F2 与 R12 共面,所以 F1、F2 与 F3 也共面。于是定理得证。利用三 力平衡汇交定理可以确定刚体在三力作用下平衡时未知力的方向。 1.2.4 作用力与反作用力定律 两物体间的作用力与反作用力总是同时存在的,且两力的大小相等、方向相反、沿着 同一直线,分别作用在两个相互作用的物体上。 这个公理概括了物体间相互作用的关系,表明作用力和反作用力总是成对出现的。 1.2.5 刚化原理 变形体在某一力系作用下处于平衡,如将此变形体刚化为刚体其平衡状态保持不变。 图 1.5 图 1.6
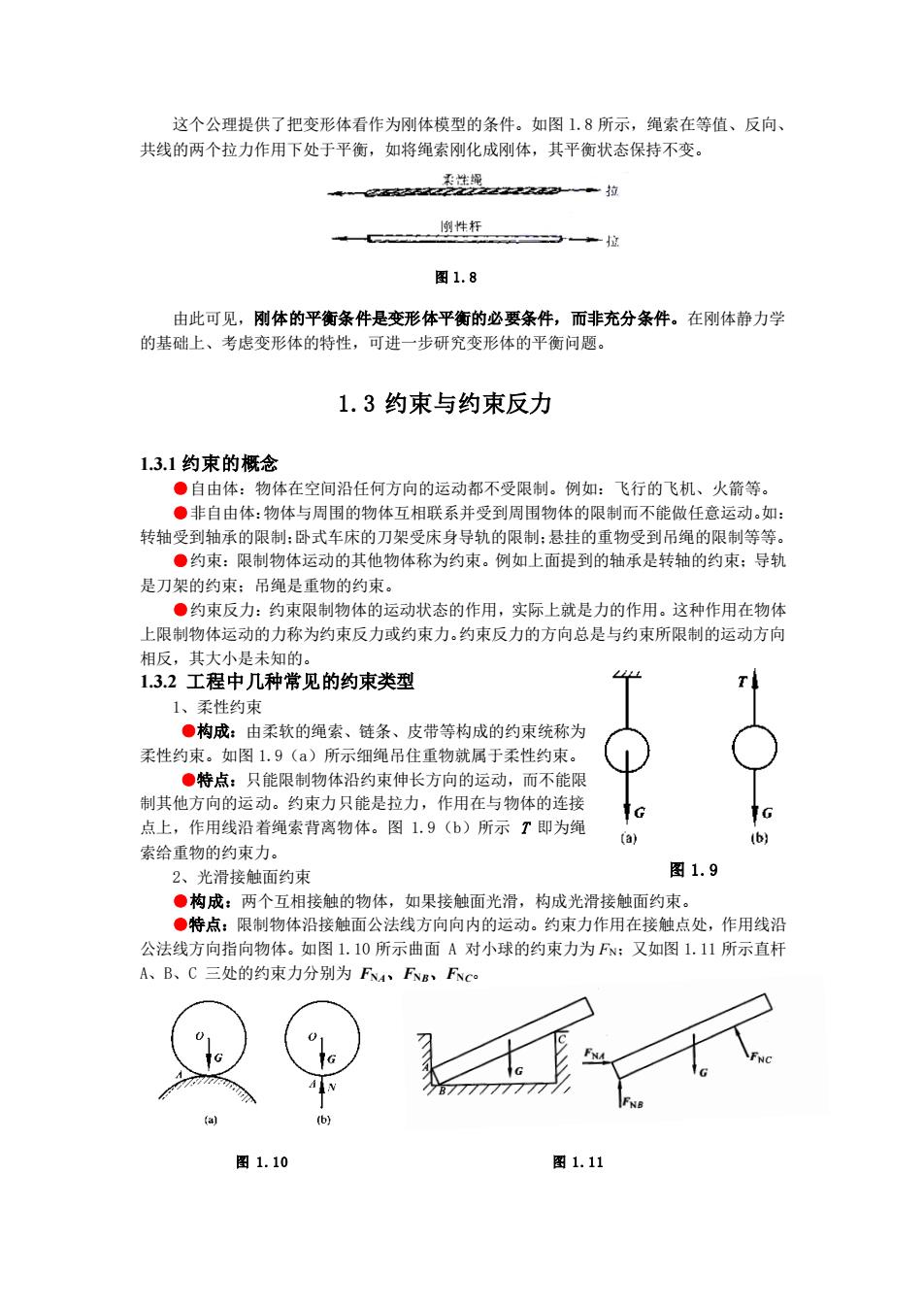
这个公理提供了把变形体看作为刚体模型的条件。如图1.8所示,绳索在等值、反向、共线的两个拉力作用下处于平衡,如将绳索刚化成刚体,其平衡状态保持不变。装连绳削性杆+一拉图1.8由此可见,刚体的平衡条件是变形体平衡的必要条件,而非充分条件。在刚体静力学的基础上、考虑变形体的特性,可进一步研究变形体的平衡问题。1.3约束与约束反力1.3.1约束的概念●自由体:物体在空间沿任何方向的运动都不受限制。例如:飞行的飞机、火箭等。·非自由体:物体与周围的物体互相联系并受到周围物体的限制而不能做任意运动。如:转轴受到轴承的限制;卧式车床的刀架受床身导轨的限制:悬挂的重物受到吊绳的限制等等。●约束:限制物体运动的其他物体称为约束。例如上面提到的轴承是转轴的约束:导轨是刀架的约束:吊绳是重物的约束。●约束反力:约束限制物体的运动状态的作用,实际上就是力的作用。这种作用在物体上限制物体运动的力称为约束反力或约束力。约束反力的方向总是与约束所限制的运动方向相反,其大小是未知的1.3.2工程中几种常见的约束类型TI1、柔性约束·构成:由柔软的绳索、链条、皮带等构成的约束统称为柔性约束。如图1.9(a)所示细绳吊住重物就属于柔性约束。·特点:只能限制物体沿约束伸长方向的运动,而不能限制其他方向的运动。约束力只能是拉力,作用在与物体的连接10G点上,作用线沿着绳索背离物体。图1.9(b)所示T即为绳(b)(a)索给重物的约束力。图1.92、光滑接触面约束构成:两个互相接触的物体,如果接触面光滑,构成光滑接触面约束。·特点:限制物体沿接触面公法线方向向内的运动。约束力作用在接触点处,作用线沿公法线方向指向物体。如图1.10所示曲面A对小球的约束力为FN:又如图1.11所示直杆A、B、C三处的约束力分别为FNA、FNB、FNC图1.10图 1. 11
图 1.9 这个公理提供了把变形体看作为刚体模型的条件。如图 l.8 所示,绳索在等值、反向、 共线的两个拉力作用下处于平衡,如将绳索刚化成刚体,其平衡状态保持不变。 由此可见,刚体的平衡条件是变形体平衡的必要条件,而非充分条件。在刚体静力学 的基础上、考虑变形体的特性,可进一步研究变形体的平衡问题。 1.3 约束与约束反力 1.3.1 约束的概念 ●自由体:物体在空间沿任何方向的运动都不受限制。例如:飞行的飞机、火箭等。 ●非自由体:物体与周围的物体互相联系并受到周围物体的限制而不能做任意运动。如: 转轴受到轴承的限制;卧式车床的刀架受床身导轨的限制;悬挂的重物受到吊绳的限制等等。 ●约束:限制物体运动的其他物体称为约束。例如上面提到的轴承是转轴的约束;导轨 是刀架的约束;吊绳是重物的约束。 ●约束反力:约束限制物体的运动状态的作用,实际上就是力的作用。这种作用在物体 上限制物体运动的力称为约束反力或约束力。约束反力的方向总是与约束所限制的运动方向 相反,其大小是未知的。 1.3.2 工程中几种常见的约束类型 1、柔性约束 ●构成:由柔软的绳索、链条、皮带等构成的约束统称为 柔性约束。如图 1.9(a)所示细绳吊住重物就属于柔性约束。 ●特点:只能限制物体沿约束伸长方向的运动,而不能限 制其他方向的运动。约束力只能是拉力,作用在与物体的连接 点上,作用线沿着绳索背离物体。图 1.9(b)所示 T 即为绳 索给重物的约束力。 2、光滑接触面约束 ●构成:两个互相接触的物体,如果接触面光滑,构成光滑接触面约束。 ●特点:限制物体沿接触面公法线方向向内的运动。约束力作用在接触点处,作用线沿 公法线方向指向物体。如图 1.10 所示曲面 A 对小球的约束力为 FN;又如图 1.11 所示直杆 A、B、C 三处的约束力分别为 FNA、FNB、FNC。 图 l.8 图 1.10 图 1.11