《工程力学》课程教学课件（PPT讲稿）第一篇 工程静力学 第4章 空间力系

第四章空间力系

1

静力学各力的作用线不在同一平面内的力系，叫空间力系，空间力系是最一般的力系。分为：空间汇交力系（α图）：空间任意力系(b图）空间平行力系(b图中去了风力）等。迎面Q1风力SYSOy工侧面PI风力NN(a)

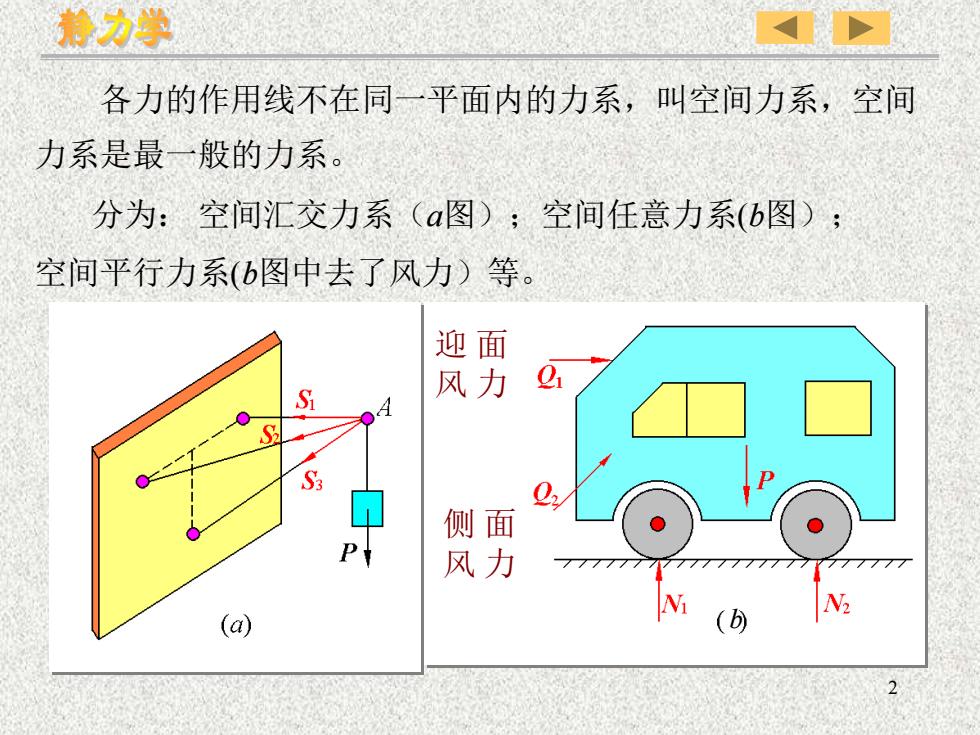
2 各力的作用线不在同一平面内的力系，叫空间力系，空间 力系是最一般的力系。 分为： 空间汇交力系（a图）；空间任意力系(b图）； 空间平行力系(b图中去了风力）等。 迎 面 风 力 侧 面 风 力 b

静力学$4-1空间汇交力系、力在空间轴上的投影与分解：Z1、一次投影法（直接投影法）已知: α,β,X=F.cos α,Y=F-cos β,Z=F-cos yy2、二次投影法（间接投影法）H已知：Φ,0xiX -F-siny-cosp=Fr-cosp-F-coso.cospY-F-siny·sin@=F-sin@=F-.coso.sinpZ-F-cosy=F.sino2

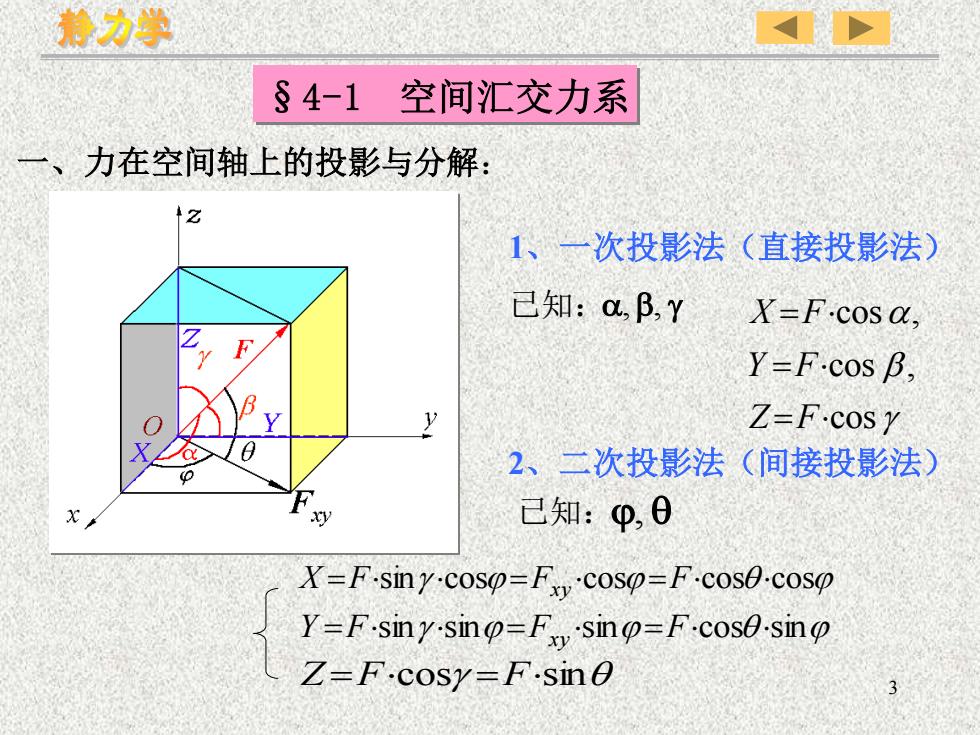
3 一、力在空间轴上的投影与分解： §4-1 空间汇交力系    cos cos , cos , =  =  =  Z F Y F X F 1、一次投影法（直接投影法） 已知： ,,  2、二次投影法（间接投影法） 已知： ,  X =Fsin cos =Fxy cos =Fcos cos Y =Fsin sin =Fxy sin =Fcos sin Z =Fcos =Fsin

静力学3、力沿坐标轴分解+Z若以F,F,F表示力沿直角坐标轴的正交分量，则：F-F+F,+FFy而:yKF6F.- Xi,F,-Yi.F -Zk七y所以:F= Xi +Yi+Zk.F=X2+Y2+Z?cosα-→.cosβ-1,.cosy-

4 3、力沿坐标轴分解： 若以 表示力沿直角 坐标轴的正交分量，则： Fx Fy Fz , , F =Fx +Fy +Fz 2 2 2 F= X +Y +Z F Z F Y F X cos= ,cos = ,cos = F Xi F Yj F Zk x = , y = , z = 而： 所以： F =Xi +Yj+Zk Fx Fy Fz

静力学二、空间汇交力系的合成：设空间汇交力系由 FF,F·..,F组成。则其合力为R-F+F2+F3+...+F, -ZF由于 F=Xi+Yi+Z,k 代入上式合力 R-ZX,i+ZYj+z,kR,-ZXR,-ZY由X，为合力在x轴的投影，.R.-Z合力投影定理合力;R-/R? +R2 +R2 =N(EX)? +(ZY)? +(Z)?00-0--号00-号RR

5 R=F1 +F2 +F3 ++Fn =F i 由于 代入上式 合力 由 为合力在x轴的投影， ∴ F X i Y j Z k i = i + i + i R X i Y j Z k = i + i + i Xi Rx =Xi Ry =Yi Rz =Zi 二、空间汇交力系的合成： 设空间汇交力系由 F1 , F2 , F3  , Fn 组成。则其合力为 ——合力投影定理 = 2 + 2 + 2 =  2 +  2 +  2 :R R R R ( X) ( Y) ( Z) 合力 x y z R R R R R Rx y z cos= ,cos == ,cos =