
第7章教学方案一一扭转扭转的概念和内力分析基本内容纯剪切圆轴扭转时横截面上的应力和强度计算圆轴扭转时的变形与刚度计算了解扭转变形的工程实例,掌握用截面法求截面上扭矩并画扭矩图教2、理解纯剪切的概念、切应力互等定理。学目3、熟练掌握圆轴扭转时横截面上的应力分布及强度计算。的、掌握圆轴扭转时的变形和扭转刚度计算。4重点圆轴扭转时横截面上的应力及扭转角的计算。、难点
第 7 章 教学方案 ——扭转 基 本 内 容 扭转的概念和内力分析 纯剪切 圆轴扭转时横截面上的应力和强度计算 圆轴扭转时的变形与刚度计算 教 学 目 的 1、了解扭转变形的工程实例,掌握用截面法求截面上扭矩并画扭 矩图。 2、理解纯剪切的概念、切应力互等定理。 3、熟练掌握圆轴扭转时横截面上的应力分布及强度计算。 4、掌握圆轴扭转时的变形和扭转刚度计算。 重 点 、 难 点 圆轴扭转时横截面上的应力及扭转角的计算
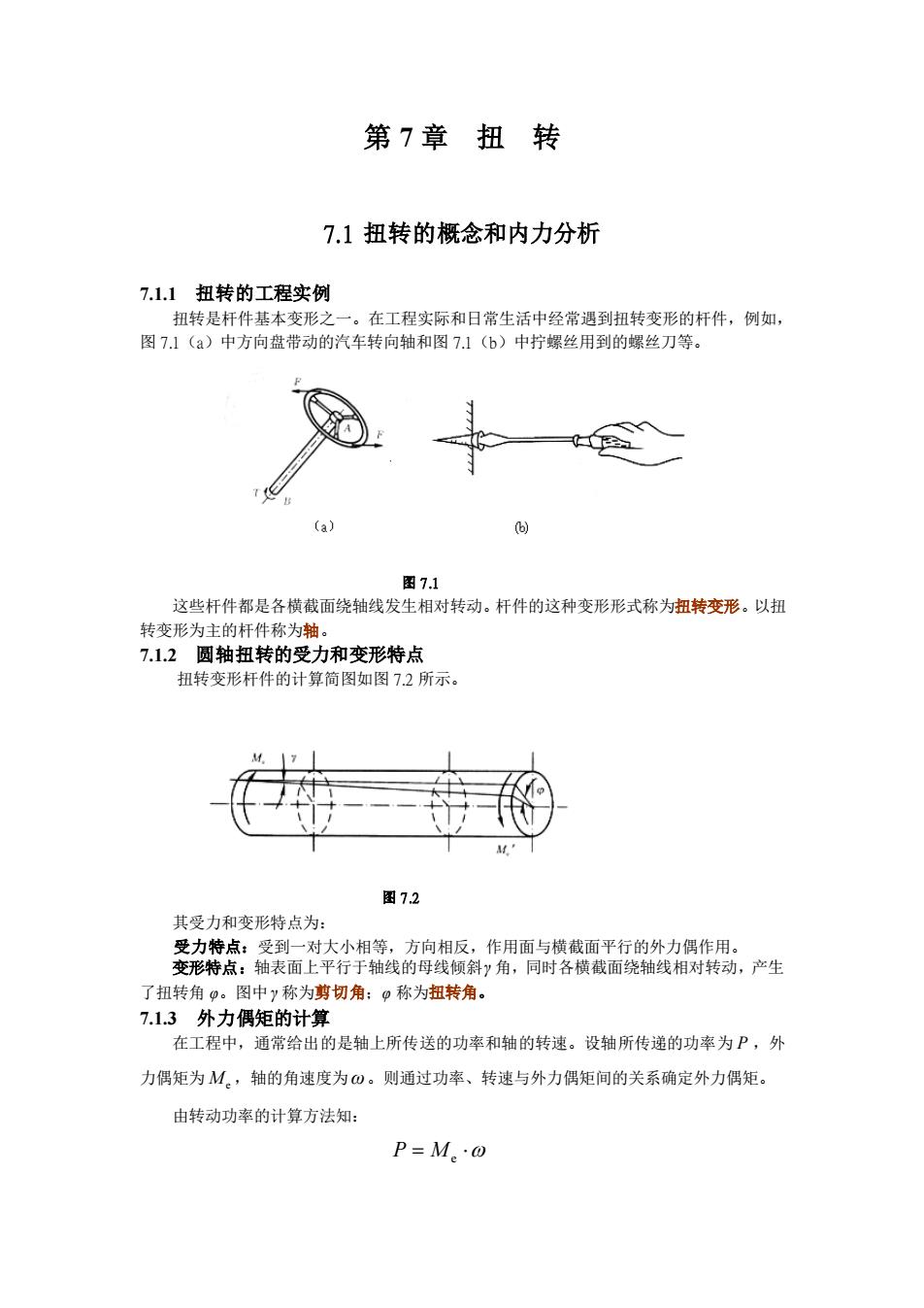
第7章扭转7.1扭转的概念和内力分析7.1.1扭转的工程实例。在工程实际和日常生活中经常遇到扭转变形的杆件,例如,扭转是杆件基本变形之图7.1(a)中方向盘带动的汽车转向轴和图7.1(b)中拧螺丝用到的螺丝刀等。5图7这些杆件都是各横截面绕轴线发生相对转动。杆件的这种变形形式称为扭转变形。以扭转变形为主的杆件称为轴。7.1.2圆轴扭转的受力和变形特点扭转变形杆件的计算简图如图7.2所示。图7.2其受力和变形特点为:受力特点:受到一对大小相等,方向相反,作用面与横截面平行的外力偶作变形特点:轴表面上平行于轴线的母线倾斜角,同时各横截面绕轴线相对转动,产生了扭转角。图中称为剪切角:称为扭转角。7.1.3外力偶矩的计算在工程中,通常给出的是轴上所传送的功率和轴的转速。设轴所传递的功率为P,外力偶矩为M。,轴的角速度为の。则通过功率、转速与外力偶矩间的关系确定外力偶矩。由转动功率的计算方法知P=M·0
第 7 章 扭 转 7.1 扭转的概念和内力分析 7.1.1 扭转的工程实例 扭转是杆件基本变形之一。在工程实际和日常生活中经常遇到扭转变形的杆件,例如, 图 7.1(a)中方向盘带动的汽车转向轴和图 7.1(b)中拧螺丝用到的螺丝刀等。 图 7.1 这些杆件都是各横截面绕轴线发生相对转动。杆件的这种变形形式称为扭转变形。以扭 转变形为主的杆件称为轴。 7.1.2 圆轴扭转的受力和变形特点 扭转变形杆件的计算简图如图 7.2 所示。 图 7.2 其受力和变形特点为: 受力特点:受到一对大小相等,方向相反,作用面与横截面平行的外力偶作用。 变形特点:轴表面上平行于轴线的母线倾斜 γ 角,同时各横截面绕轴线相对转动,产生 了扭转角 φ。图中 γ 称为剪切角;φ 称为扭转角。 7.1.3 外力偶矩的计算 在工程中,通常给出的是轴上所传送的功率和轴的转速。设轴所传递的功率为 P ,外 力偶矩为 Me ,轴的角速度为 ω 。则通过功率、转速与外力偶矩间的关系确定外力偶矩。 由转动功率的计算方法知: P = Me

故:M.=上式中功率P的单位为瓦(w),角速度的单位为弧度/秒(rad/s)。若取工程中常用单位功率为千瓦(kW),力偶矩为牛米(N·m),转速n为转/分(r/min)。做单位变换,代入上式,得M。=9549(N·m)(7-1)7.1.4 扭转时横截面上的扭矩和扭矩图图7.3(a)所示为一受扭圆轴,若欲求m-m横截面上的内力,则可假想地用一平面沿m-m截面将该轴分为I、IⅡI两部分如图7.3(b)(c)所示。若取左段1研究,由该段的平衡方程可知,在m-m截面上必存在一个转向与外力偶M,相反的内力偶T。列平衡方程0.00-I店00图 7.3 T-M,=0T=M.式中T为m-m截面上的内力偶矩,称为扭矩,它是I、IⅡI两部分m-m截面上相互作用的分布内力系的合力偶矩扭矩T的符号规定如下:若按右手螺旋法则把T表示为矢量,当矢量方向与截面的外法线方向一致时,T为正:反之为负如果作用于轴上的外力偶多于两个,外力偶将轴分成若干段,各段横截面上的扭矩不尽相同,则需分段求出扭矩。为了表示沿轴线各截面的扭矩变化情况,用扭矩图来表示。【例7-1】图7.4(a)所示轴,已知转速n=955r/min,功率由轮B输入,Pg=100kW通过轮A、C输出,PA=40kW,P。=60kW,试作轴的扭矩图。解:(1)外力偶矩计算由式(7-1)得100Mg=9549=9549×=1000N.m955×40 =400N·mMA =9549 PA =9549x955
故: P M e = 上式中功率 P 的单位为瓦(w),角速度的单位为弧度/秒(rad/s)。若取工程中常用单位: 功率为千瓦( kW ),力偶矩为牛米( Nm ),转速 n 为转/分( r/min )。做单位变换,代 入上式,得 n P M e = 9549 ( Nm ) (7-1) 7.1.4 扭转时横截面上的扭矩和扭矩图 图 7.3(a)所示为一受扭圆轴,若欲求 m−m 横截面上的内力,则可假想地用一平面 沿 m−m 截面将该轴分为 I、II 两部分如图 7.3(b),(c)所示。若取左段 I 研究,由该段的平 衡方程可知,在 m−m 截面上必存在一个转向与外力偶 Me 相反的内力偶 T。列平衡方程 图 7.3 e e 0 T M T M = − = 式中 T 为 m−m 截面上的内力偶矩,称为扭矩,它是 I、II 两部分 m−m 截面上相互 作用的分布内力系的合力偶矩。 扭矩 T 的符号规定如下:若按右手螺旋法则把 T 表示为矢量,当矢量方向与截面的外 法线方向一致时, T 为正;反之为负。 如果作用于轴上的外力偶多于两个,外力偶将轴分成若干段,各段横截面上的扭矩不 尽相同,则需分段求出扭矩。为了表示沿轴线各截面的扭矩变化情况,用扭矩图来表示。 【例 7-1】 图 7.4(a)所示轴,已知转速 n = 955r/min ,功率由轮 B 输入, PB =100kW , 通过轮 A 、C 输出, PA = 40kW,PC = 60kW ,试作轴的扭矩图。 解:(1)外力偶矩计算 由式(7-1)得 1000N m 955 100 9549 9549 B B = = = n P M 400N m 955 40 9549 9549 A A = = = n P M
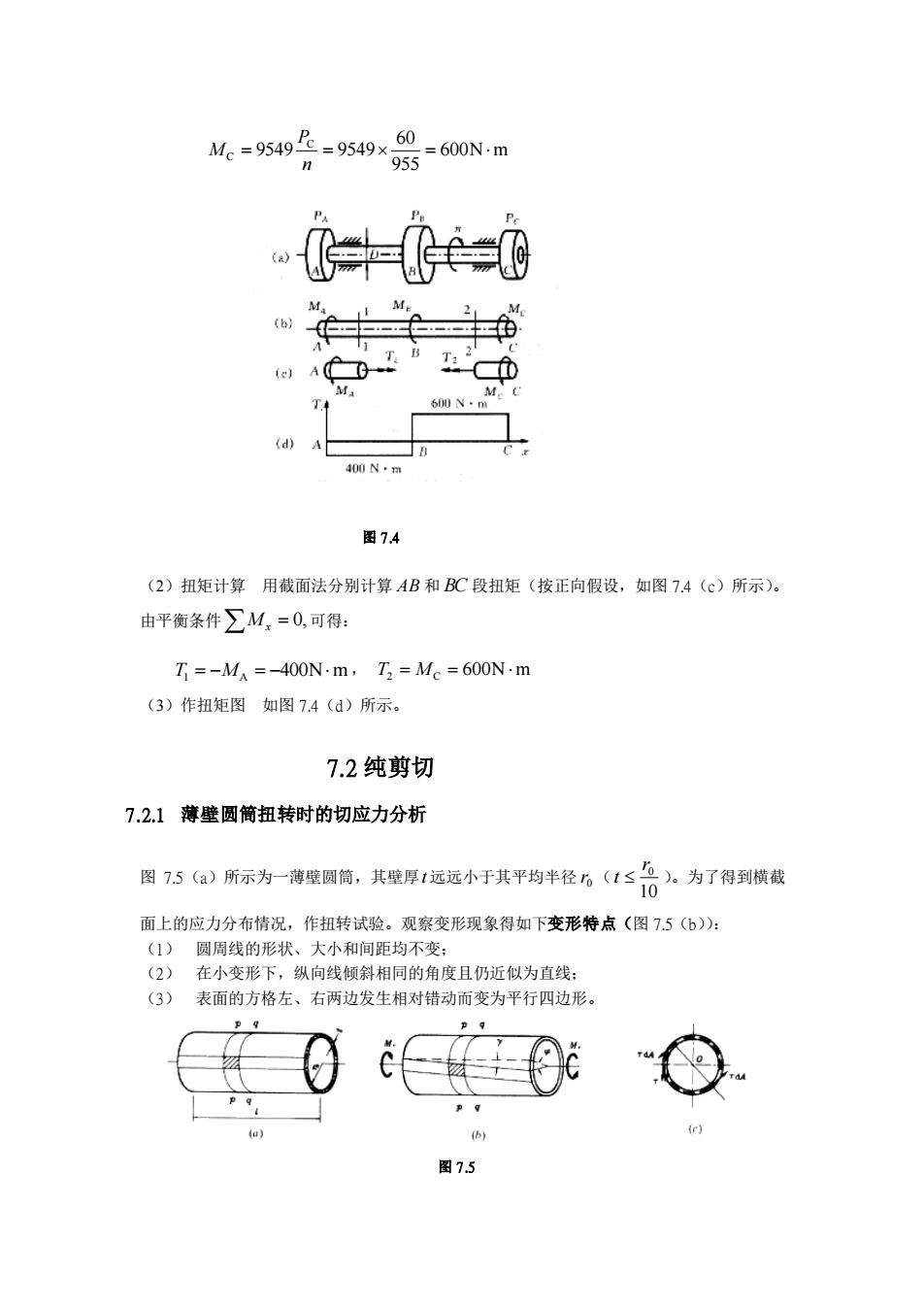
60 = 600N·mMe=9549= 9549×955中兰ACT1M400Nm图 7.4(2)扭矩计算用截面法分别计算AB和BC段扭矩(按正向假设,如图7.4(c)所示)。由平衡条件M,=0,可得:T =-M^=-400N-m, T, =Mc= 600N.m(3)作扭矩图如图7.4(d)所示。7.2纯剪切7.2.1 薄壁圆简扭转时的切应力分析图7.5(a)所示为一薄壁圆筒,其壁厚t远远小于其平均半径r(t≤)。为了得到横截面上的应力分布情况,作扭转试验。观察变形现象得如下变形特点(图7.5(b)):(D)圆周线的形状、大小和间距均不变;(2)在小变形下,纵向线倾斜相同的角度且仍近似为直线:(3)表面的方格左、右两边发生相对错动而变为平行四边形。0图 7.5
600N m 955 60 9549 9549 C C = = = n P M 图 7.4 (2)扭矩计算 用截面法分别计算 AB 和 BC 段扭矩(按正向假设,如图 7.4(c)所示)。 由平衡条件 = 0, Mx 可得: T1 = −MA = −400Nm, T2 = MC = 600Nm (3)作扭矩图 如图 7.4(d)所示。 7.2 纯剪切 7.2.1 薄壁圆筒扭转时的切应力分析 图 7.5(a)所示为一薄壁圆筒,其壁厚 t 远远小于其平均半径 0 r ( 10 0 r t )。为了得到横截 面上的应力分布情况,作扭转试验。观察变形现象得如下变形特点(图 7.5(b)): (1) 圆周线的形状、大小和间距均不变; (2) 在小变形下,纵向线倾斜相同的角度且仍近似为直线; (3) 表面的方格左、右两边发生相对错动而变为平行四边形。 图 7.5

结论:当薄壁圆简扭转时,其横截面及包含轴线的纵向截面上都没有正应力,横截面上只有切应力t。因为筒壁的厚度1很小,可以认为沿壁厚切应力均匀分布。又由于在同一圆周上各点变形相同,应力也就相同,方向沿圆周切线方向,如图7.5(c)所示。横截面上切应力t的合力为横截面上的扭矩T,即:T=JrotdA-f"rot rdo=2.rot-t战(7-2)2-2元.17.2.2纯剪切的概念、切应力互等定理用相邻的两个横截面p-p和q-g和两个纵向截面,从圆筒中取出边长分别为dxdy和t的微小六面体,称之为单元体,如图7.6所示。单元体左、右两侧面是圆筒横截面的部分,其上应力数值相等但方向相反,形成了一个力偶,力偶矩为(ttdy)dx。由于圆筒平衡,单元体必也平衡。为保持其平衡,单元体的上、下两个侧面上必然有切应力,且大小相等方向相反,组成一个与(ttdy)dx相平衡的力偶。设上、下两个侧面上的切应力为t,由ZM,=0得:(t -tdy)dx =(t'tdx)dy所以T=T图7.6即:在相互垂直的一对平面上,切应力同时存在,数值相等,且都垂直于两个平面的交线,方向共同指向或共同背离这一交线。这就是切应力互等定理。单元体的上、下、左、右四个侧面上,只有切应力而无正应力,这种应力状态称为纯剪切。7.2.3剪切胡克定律实验可得,在弹性变形范围内,切应力与切应变成正比,其关系可表示为(7-3)T=G其中G为材料的剪切弹性模量或称切变模量式(7-3)称为剪切胡克定律,即在剪切弹性范围内,切应变与切应力T成正比。至此,已经介绍了三个与材料有关的弹性常数E、Ⅱ、G,对各向同性材料,三者的关系为
结论:当薄壁圆筒扭转时,其横截面及包含轴线的纵向截面上都没有正应力,横截面上只 有切应力 τ 。 因为筒壁的厚度 t 很小,可以认为沿壁厚切应力均匀分布。又由于在同一圆周上各点变 形相同,应力也就相同,方向沿圆周切线方向,如图 7.5(c)所示。横截面上切应力 τ 的合 力为横截面上的扭矩 T ,即: = = = T r A r r r t A 2 0 0 2 0 0 d 0 d 2 故: r t T 2 2 0 = (7-2) 7.2.2 纯剪切的概念、切应力互等定理 用相邻的两个横截面 p − p 和 q − q 和两个纵向截面,从圆筒中取出边长分别为 dx,dy 和 t 的微小六面体,称之为单元体,如图 7.6 所示。单元体左、右两侧面是圆筒横截面的一 部分,其上应力数值相等但方向相反,形成了一个力偶,力偶矩为 (τtdy)dx 。由于圆筒平衡, 单元体必也平衡。为保持其平衡,单元体的上、下两个侧面上必然有切应力,且大小相等、 方向相反,组成一个与 (τtdy)dx 相平衡的力偶。设上、下两个侧面上的切应力为 / τ ,由 Mz = 0 得: ( tdy)dx ( tdx)dy / = 所以 / = 图 7.6 即:在相互垂直的一对平面上,切应力同时存在,数值相等,且都垂直于两个平面的交线, 方向共同指向或共同背离这一交线。这就是切应力互等定理。 单元体的上、下、左、右四个侧面上,只有切应力而无正应力,这种应力状态称为纯剪 切。 7.2.3 剪切胡克定律 实验可得,在弹性变形范围内,切应力与切应变成正比,其关系可表示为: = G (7-3) 其中 G 为材料的剪切弹性模量或称切变模量。 式(7-3)称为剪切胡克定律,即在剪切弹性范围内,切应变 γ 与切应力 τ 成正比。 至此,已经介绍了三个与材料有关的弹性常数 E 、μ、 G ,对各向同性材料,三者的 关系为